Погрешности измерений в лабораторных работах

Погрешности принято подразделять на грубые (промахи), систематические и случайные при проведении прямых (непосредственных) измерений какой-либо физической величины.

Будем считать, что:

1. Грубые погрешности исключены;

2. Поправки, которые следовало определить (например, смещение нулевого деления шкалы) вычислены и внесены в окончательные результаты;

3. Систематические погрешности определяются неточностью средства измерения и указаны в его техническом паспорте. Знак этой погрешности заранее неизвестен, поэтому её необходимо учитывать в окончательном результате измерений.

4. Случайные погрешности уменьшаются при увеличении числа измерений. Пусть проведены n измерений величины x. Тогда за лучшую оценку истинного значения принимается среднее арифметическое отдельных измерений

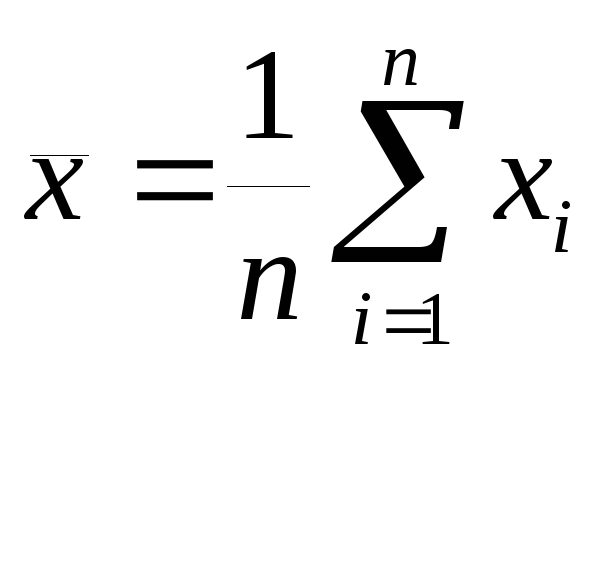(1)

где: x_i - результат i–го измерения.

Для оценки случайной погрешности существует несколько способов. Наиболее распространенная так называемая средняя квадратичная погрешность среднего арифметического

(2)

Пусть P означает вероятность того, что результат измерений отличается от истинного на величину ∆x , где ∆x - суммарная погрешность измерения данной величины: абсолютная погрешность. Тогда можно записать

где x_ист – истинное значение измеряемой величины, которое заранее неизвестно.

Вероятность P называется доверительной вероятностью, а интервал от до - доверительным интервалом.

Если ограничиться учётом только случайных погрешностей, то при небольшом числе измерений полуширина доверительного интервала равна

(3)

где t_P,n – коэффициенты Стьюдента, которые табулированы в зависимости от P и n. В наших работах установим P = 0,95. Тогда при n = 3 t_0,95;4 = 4,3, при n = 4 t_0,95;4 = 3,2, при n = 5 t_0,95;5 = 2,8.

Будем считать, что систематическая погрешность определяется, в основном погрешностью средства измерения. Для аналоговых электроизмерительных приборов – это класс точности (указывается на приборе)

(4)

где ∆x_пр - наибольшая абсолютная погрешность прибора; x_N – предельное значение шкалы прибора.

Из (4) следует, что

(5)

Погрешности цифровых измерительных приборов даются в паспорте каждого из них.

При многократных измерениях среднеквадратическое значение инструментальной погрешности P = 0,95 определяется по формуле:

(6)

Если при нескольких измерениях устойчиво получаются одни и те же результаты, то за ∆x_си можно принять половину цены деления шкалы или половину единицы цифры последнего разряда результата.

Относительная погрешность результата находится по формуле

(7)

или часто в процентах

(8)

Таким образом предлагается следующий порядок операций при прямых измерениях.

1. Вычисляется среднее арифметическое из n измерений:

2. Определяется средняя квадратичная погрешность среднего арифметического:

3. Находится

4. Определяется абсолютная погрешность результата измерений

5. Оценивается относительная погрешность результата измерений

6. Окончательный результат записывается в виде

; P = 0,95, n = 3÷5.

Погрешности косвенных измерений

Пусть измеряемая величина является функцией непосредственно измеряемых величин

(9)

Теория погрешностей определяет, что абсолютная погрешность ∆y находится по формуле

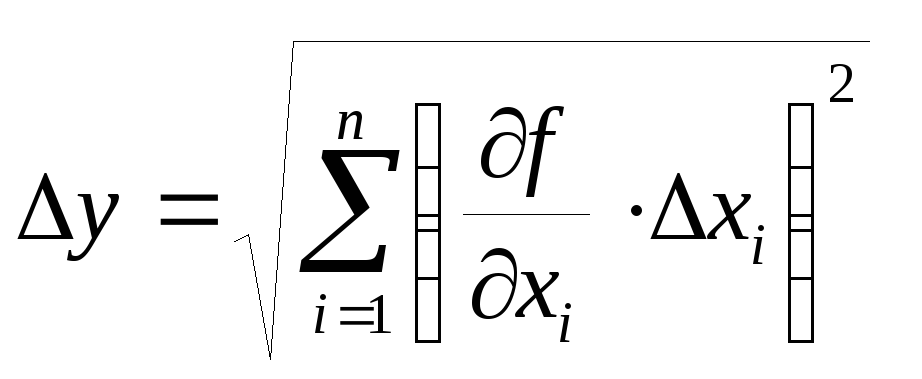(10)

где ∂f/∂x_i обозначает так называемую частную производную, т. е. производная, которая вычисляется от функции f по аргументу x_i, причём все остальные аргументы считаются постоянными.

Если измеряемые величины x_i входят в основную формулу в виде произведения, то удобно определить вначале относительную погрешность по формуле

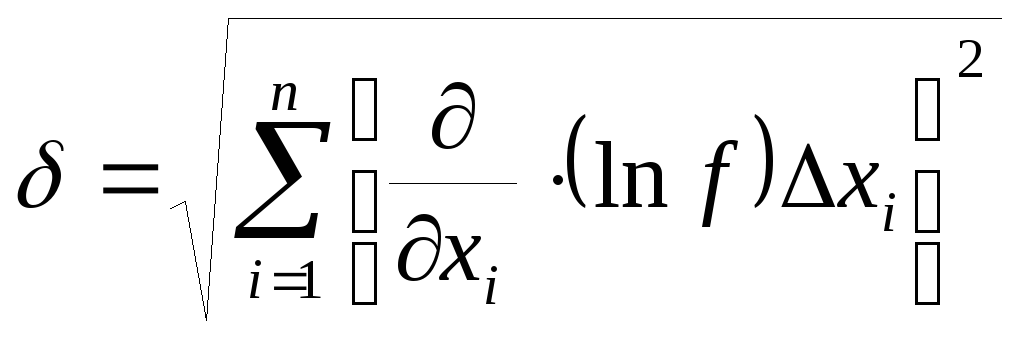(11)

а затем найти и

Рассмотрим применение формул (10) и (11) на примерах.

Пусть

.

и по формуле (10)

,

причём ∆x₁ и ∆x₂ определены предварительно по формуле (4).

Пусть

.

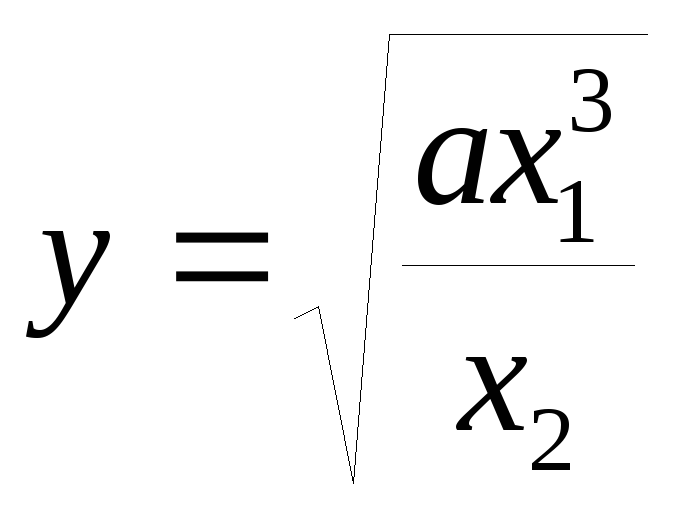В этом случае сначала найдём натуральный логарифм, а затем – частичные производные:

Подставляем в (11), найдём

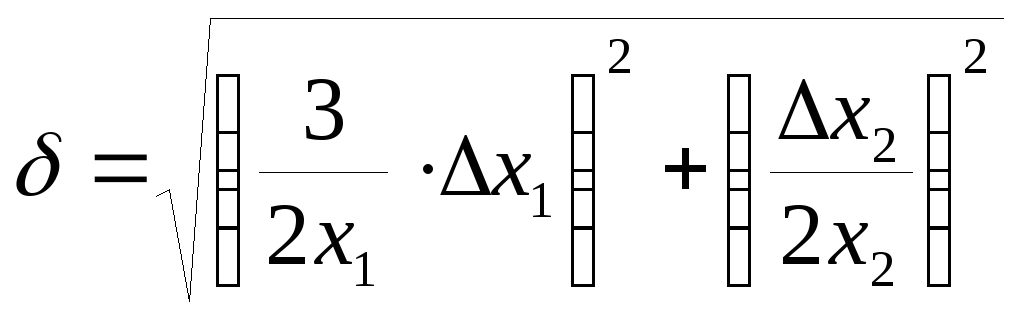
Нетрудно видеть, что предварительное логарифмирование существенно упрощает вид частных производных.

Возможен и другой подход к оценке погрешности результата косвенного измерения. Вместо определения искомой величины через среднее значение

Можно для каждого выполненного опыта вычислить

а затем найти как среднее арифметическое и далее абсолютную погрешность по формуле (3).

Оба способа дают близкие результаты.

Пусть, например, находится плотность цилиндрического тела:

ρ = 4m / πD²H,

причем непосредственно определяется три раза диаметр цилиндра D_i и его высота Н_i (i = 1, 2, 3). Тогда можно подсчитать

ρ_i = 4m / πD²_iH_i.

для каждого из трех измерений.

Среднее значение плотности можно найти, как обычно, по формуле:

<ρ> =∑ρ_i /3,

а абсолютная погрешность определяется как

Δρ = 4,3√[∑(<ρ> – ρ_i) /6].

Таблица 1.

Коэффициенты Стьюдента.

P = 0,68		P = 0,95		P = 0,99
n	t P,n	n	t P,n	n	t P,n
2	2,0	2	12,7	2	63,7
3	1,3	3	4,3	3	9,9
4	1,3	4	3,2	4	5,8
5	1,2	5	2,8	5	4,6
6	1,2	6	2,6	6	4,0
7	1,1	7	2,4	7	3,7
8	1,1	8	2,4	8	3,5

Округление результата

Результат измерения округляется по следующим правилам:

1. Абсолютная погрешность берётся с двумя значащими цифрами, если первая из них 1 или 2.

Абсолютная погрешность берётся с одной значащей цифрой, если она больше или равна 3.

Это правило вытекает из законов математической статистики, так как оказывается, что даже при 10 измерениях относительная погрешность самой погрешности превышает 3 % (30% от 2 составляет 0,6; а, например, от 4 – 1,2, что превышает единицу первого разряда).

2. Числовое значение результата измерений должно оканчиваться цифрой того же порядка, что и числовое значение абсолютной погрешности.

3. Если первая отбрасываемая цифра больше или равна 5, то последняя сохраняемая цифра увеличивается на единицу.

4. Если отбрасываемая цифра меньше 5, то последняя сохраняемая цифра остаётся без изменений.

5. При округлении целых чисел все цифры, отброшенные при округлении, заменяют множителем 10^m, где m – число от брошенных цифр. Например, при округлении до двух значащих цифр число 31127 примет вид 31×10³.

6