
теория вероятности
.pdf
(6.5).
Заметим также, что в случае нахождения вероятности попадания непрерывной с.в. в бесконечный интервал по формуле F(b) F(a) будут возникать конструкции, условно записываемые как F( ) и F( ). Понимать их нужно следующим образом:
F( ) lim |
F(x) 0, F( ) lim F(x) 1. |
x |
x |
Определение 6.2. Математическим ожиданием непрерывной случайной величины называется число, которое вычисляется по формуле
M xf (x)dx |
(6.6) |
|
|
Определение 6.3. Дисперсией непрерывной случайной величины называется число D M( M )2 , которое удобно вычислять по формуле
D M 2 (M )2 , или D x2 f (x)dx (M )2 (6.7)
Пример 6.1.
Дана функция распределения F(x) непрерывной случайной величины :
0, |
x 0, |
|
|
|
|
|
|
0 x 2, |
|
|
|
F(x) ax2 , |
|
|
|||
|
x 2. |
|
|
|
|
1, |
D , |
|
|
||
Найти: a, |
f (x), M , |
P(0 1), |
P( 1 2). |
||
Решение:
Определим a из условия непрерывности F(x) при любых значениях x. Ясно, что внутри каждого из интервалов F(x) непрерывна, поэтому осталось использовать непрерывность
48
III. Условная вероятность. Теоремы сложения и умножения вероятностей.
Формула полной вероятности.
Определение 3.1. Два события называются несовместными, если они не могут произойти вместе (или одновременно). Другими словами, два события несовместны, если их произведение является невозможным событием:
A и B несовместны A B .
При вычислении вероятности суммы событий прежде всего нужно выяснить, совместны события или нет. Если события попарно несовместны (т.е. любые два из них не могут произойти одновременно), то вероятность их суммы равна сумме вероятностей всех отдельных событий:
P(A B) P(A) P(B), если A B ,
P(A B C) P(A) P(B) P(C), если AB AC BC ,
P(A1 A2 An ) P(A1) P(A2 ) P(An ), если
Ai Aj при i j.
Если же события являются совместными, то формулы для вероятности их суммы резко усложняются. Только в случае двух совместных событий формула имеет более-менее компактный вид:
P(A B) P(A) P(B) P(A B).
Уже в случае трех событий (не говоря о большем количестве) она становится настолько громоздкой, что ею практически не пользуются:
P(A B C) P(A) P(B) P(C) P(AB) P(AC)P(BC) P(ABC).
Определение 3.2. Вероятность события A при условии, что произошло событие B обозначается P(A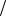 B) или PB (A) и называется условной вероятностью.
B) или PB (A) и называется условной вероятностью.
21
www.mitht.ru/e-library

Пример 3.1.
В урне имеется 5 белых и 7 черных шаров. Из урны по очереди вынимают два шара (без возвращения). События A1 –
первый шар белый, A2 – второй шар белый.
Тогда P(A2  A1) 4
A1) 4 11 (если событие A1 произошло, т.е. первый вынутый шар был белым, то в урне осталось 4 белых и 7 черных шаров и P(A2
11 (если событие A1 произошло, т.е. первый вынутый шар был белым, то в урне осталось 4 белых и 7 черных шаров и P(A2  A1) вычисляется по класси-
A1) вычисляется по класси-
ческой схеме). Аналогично вычисляется P(A2  A1) 5
A1) 5 11). Определение 3.3. События A и B называются независимыми, если условная вероятность одного из них при условии, что второе произошло, такая же, как и при условии, что второе не произошло (а, значит, и без всяких условий относительно второго события):
11). Определение 3.3. События A и B называются независимыми, если условная вероятность одного из них при условии, что второе произошло, такая же, как и при условии, что второе не произошло (а, значит, и без всяких условий относительно второго события):
P(A B) P(A
B) P(A B) P(A).
B) P(A).
Замечание: Для проверки независимости событий A и B достаточно проверить в последней формуле одно из равенств.
Скажем, события A1 и A2 в примере 3.1 зависимые, т.к.
P(A2  A1) P(A2
A1) P(A2  A1) .
A1) .
При вычислении вероятности произведения событий прежде всего нужно выяснить, зависимые события или нет. Если события независимые, то вероятность их произведения равна произведению вероятностей всех отдельных событий: P(AB) P(A) P(B), если A и B – независимы,
P(ABC) P(A) P(B) P(C), если A, B и C – независимы, и т.д.
Если же события зависимые, то вероятность произведения вычисляется по более сложным формулам, в которые входят условные вероятности:
P(AB) P(A) P(B A);
A);
P(ABC) P(A) P(B A) P(C
A) P(C AB); 22
AB); 22
Ясно, что функция распределения F(x) тоже будет задаваться различными формулами, но на тех же интервалах, что и плотность f (x). Из (6.1) следует, что функция распределения F(x) является одной из первообразных плотности f (x). Находим на каждом интервале первообразную от плотности (не забудем про произвольные постоянные, которые на каждом интервале свои!). Затем находим произвольные постоянные на крайних интервалах из соотношений
lim F(x) 0; lim F(x) 1, а на остальных интервалах – из
x x
условия непрерывности функции распределения в точках «склейки» этих интервалов. Оба подхода рассматриваются в примере 6.2.
Если случайная величина непрерывна, то ее возможные значения заполняют целиком некоторый конечный или бесконечный интервал, и вероятность того, что примет
конкретное значение x0 , равна нулю, т.е. P( x0 ) 0. По-
этому для непрерывной случайной величины вероятности попадания в интервал можно вычислить по формулам:
P(a b) P(a b) P(a b)
b
P(a b) f (x)dx F(b) F(a) |
(6.5) |
a |
|
Из двух вариантов формулы, разумеется, |
проще тот, |
где вероятность попадания непрерывной с.в. в интервал выражается через функцию распределения F(x): гораздо легче вычислить F(b) F(a), чем интегрировать. Но это при условии, что функция распределения F(x) известна! Если же известна только плотность распределения f (x), то нахождение функции распределения F(x) является, как отмечено выше, достаточно непростой задачей – во всяком случае, явно более сложной, чем вычисление интеграла в формуле
47
www.mitht.ru/e-library

VI. Непрерывная случайная величина и ее характеристики.
Определение 6.1. Случайная величина называется непрерывной, если ее функция распределения F(x) непрерывна.
Производная от функции распределения (при условии, что она существует при всех x R, за исключением, может быть, конечного числа точек) называется плотностью рас-
пределения и обозначается |
f (x): |
|
(6.1) |
f (x) F (x) |
Т.к. плотность распределения является производной
неубывающей функции F(x), то она неотрицательна: |
|
f (x) 0 |
(6.2) |
Еще одно (основное) свойство плотности распределе- |
|
ния любой непрерывной с.в. выражается формулой |
|
|
|
f (x)dx 1 |
(6.3) |
|
|
Задача нахождения плотности распределения по известной функции распределения решается очень легко по формуле (6.1). При решении обратной задачи, т.е. нахождении функции распределения по известной плотности распределения, возможно два подхода.
Первый подход основан на формуле, непосредственно выражающей функцию распределения F(x) через плотность распределения f (x):
x
|
F(x) f (t)dt |
(6.4) |
|
|
|
Эта |
формула удобна для использования, если плотность |
|
f (x) |
задана одной формулой при всех x R. Если же f (x) |
|
задана различными формулами на различных интервалах, то можно поступить так (второй подход):
46
и т.д. (каждый следующий множитель есть условная вероятность следующего события при условии, что произошли все предыдущие).
Пример 3.2.
В условиях примера 3.1 вычислить вероятность события A1A2 (оба вынутых шара белые)
Решение:
Как было установлено в примере 3.1, события A1 и A2 – зависимые, следовательно:
P(A A ) P(A ) P(A A ) 5 4 5 . |
|||||||
1 |
2 |
1 |
2 |
1 |
12 |
11 |
33 |
Как уже говорилось выше, вычисление вероятности суммы совместных событий производится по очень громоздкой формуле, при количестве слагаемых, большем двух. Однако имеется одна ситуация (часто встречающаяся на практике), когда вычислить вероятность суммы совместных событий можно относительно просто.
Вычисление вероятности суммы совместных, но независимых событий.
Если события A и B совместны, но независимы, то
воспользуемся формулой де Моргана A B A B, а также
тем фактом, что если A и B независимы, то A и B тоже независимы (заметим, кстати, хотя к рассматриваемой си-
туации это отношения не имеет, что точно также A и B, A и B независимы).
P(A B) 1 P(A B) 1 P(A B) 1 P(A) P(B) .
Аналогично, для трех совместных, но независимых событий:
P(A B C) 1 P(A) P(B) P(C) |
и т.д. |
Пример 3.3.
Для трех стрелков известны вероятности поражения мишени
23
www.mitht.ru/e-library

каждым: 0,5 – для первого, 0,8 – для второго и 0,6 – для третьего. Все три одновременно стреляют по одной и той же мишени. Найти вероятности следующих событий:
A– произошло три попадания в мишень;
B– произошло два попадания в мишень;
C– мишень поражена (произошло хотя бы одно попадание
вмишень);
D – произошло не менее двух попаданий в мишень.
Решение: |
i-й стрелок попал в мишень, |
||||||
Пусть событие Si ,i 1,2,3 – |
|||||||
тогда, соответственно, |
|
– |
i-й стрелок промахнулся, и по |
||||
Si |
|||||||
условию: P(S1) 0,5, P(S2 ) 0,8, P(S3) 0,7, откуда: |
|||||||
P( |
|
) 1 P(S1) 0,5, |
P( |
|
) 1 P(S2 ) 0,2, |
||
S1 |
S2 |
||||||
P(S3) 1 P(S3) 0,4.
Интересующие нас события выражаются через S1 ,S2 и S3
следующим образом:
A S1S2S3 ;
B S1S2 S3 S1S2S3 S1S2S3 ; C S1 S2 S3 ;
D A B .
Ясно также, что события S1 ,S2 и S3 независимые, но совме-
стные, поэтому:
P(A) P(S1S2S3) P(S1) P(S2 ) P(S3) 0,5 0,8 0,6 0,24;
P(C) P(S1 S2 S3 ) 1 P(S1) P(S2 ) P(S3 )
1 0,5 0,2 0,4 0,96
При вычислении вероятности события B заметим, что все три слагаемые несовместны (например, события S1S2 S3
и S1S2S3 несовместны потому, что первое из них предпола-
24
Задача 5.9.
По данным ОТК на 100 заготовленных деталей приходится 30 с дефектом, а 70 – без дефекта. Найти вероятность того, что среди наудачу взятых 7 деталей окажется не более двух без дефекта.
Задача 5.10.
Вероятность того, что телевизор требует ремонта в течение гарантийного срока, равна p 0,2. Найти вероятность того, что в течение гарантийного срока из 6 телевизоров:
а) не более одного потребует ремонта; б) ни один не потребует ремонта; в) хотя бы один потребует ремонта.
Задача 5.11.
В сфере радиуса r находятся n молекул газа. Найти вероятность того, что из них ровно m молекул будут находиться на расстоянии, меньшем r от центра сферы (m n , 1)
Задача 5.12.
Вероятность производства бракованной детали равна 0,008. Найти вероятность того, что в партии из 1000 будет 8 бракованных.
Задача 5.13.
Вероятность изготовления бракованного изделия равна 0,02. Вычислить вероятность того, что контролер, проверяющий 100 изделий, обнаружит среди них m бракованных (m 0,1,2,3). Вычисления производить по формулам Бернулли и Пуассона до четвертого десятичного знака. Сравнить результаты.
Задача 5.14.
Радиоактивное вещество за промежуток времени 7,5 сек. испускает в среднем 3,87 - частицы. Найти вероятность того, что за 1 сек. это вещество испустит хотя бы одну - частицу.
45
www.mitht.ru/e-library

Задача 5.3.
Вероятность попадания стрелком в десятку равна 0,7 , а в девятку – 0,3. Определить вероятность того, что данный стрелок при трёх выстрелах наберёт не менее 29 очков.
Задача 5.4.
Прибор выходит из строя, если перегорят не менее пяти ламп типа A или не менее двух ламп типа B . Определить вероятность выхода из строя прибора, если известно, что перегорели пять ламп, а вероятности перегорания ламп типов A и B равны соответственно 0,7 и 0,3 (выход из строя ламп разных типов – события независимые).
Задача 5.5.
Вероятность того, что расход электроэнергии на заводе не будет превышать 10000 кВт. ч. в рабочий день, равна 3 4. Найти вероятность того, что из 6 рабочих дней недели окажется m дней (m 0,1,2,3,4,5,6), в течение которых произойдет перерасход электроэнергии.
4. Найти вероятность того, что из 6 рабочих дней недели окажется m дней (m 0,1,2,3,4,5,6), в течение которых произойдет перерасход электроэнергии.
Задача 5.6.
В нефтеносном районе бурят одновременно 6 скважин. Каждая скважина вскрывает месторождение независимо от других с вероятностью 0,05. Какова вероятность вскрытия месторождения? Сколько скважин нужно пробурить, чтобы вероятность вскрытия месторождения превысила 0,5?
Задача 5.7.
В партии из 100 бурильных труб содержится 5% бракованных. Какова вероятность, что среди выбранных наудачу 10 труб окажется две бракованные трубы?
Задача 5.8.
Вероятность выиграть по одному билету лотереи равна 1 7. Какова вероятность, имея 6 билетов, выиграть:
7. Какова вероятность, имея 6 билетов, выиграть:
а) по двум билетам; б) по трем билетам; в) не выиграть ни по одному билету.
44
гает, что S2 произошло, а второе, что S2 не произошло – ясно, что одновременно этого быть не может). Таким образом:
P(B) P(S1S2 S3 S1 S2S3 S1S2S3 ) P(S1S2 S3) P(S1 S2S3)
P(S1S2S3 ) P(S1)P(S2 )P(S3 ) P(S1)P(S2 )P(S3 )
P(S1)P(S2 )P(S3 ) 0,5 0,8 0,4 0,5 0,2 0,6 0,5 0,8 0,6
0,16 0,06 0,24 0,46
Наконец, при вычислении вероятности события D заметим, что события A и B несовместные (первое из них предполагает, что не было ни одного промаха, а второе – что был один промах), поэтому
P(D) P(A B) P(A) P(B) 0,24 0,46 0,7.
Дополнительный материал.
Определение 3.3. События H1,H2, ,Hn образуют полную группу событий, если они попарно несовместны и их сумма является достоверным событием: H1 H2 Hn .
n
Ясно, что P(Hi ) 1.
i 1
Если события H1,H2, ,Hn образуют полную группу
событий, то вероятность любого события A может быть вычислена по формуле:
n |
n |
|
P(A) P(AHi |
) P(A Hi)P(Hi ) |
(3.1) |
i 1 |
i 1 |
|
Формула (3.1) называется формулой полной вероятности.
Пример 3.4.
С первого автомата на сборку поступает 10%, со второго – 40%, с третьего – 50% деталей. Первый автомат дает в среднем 0,2% брака, второй – 0,3% брака, третий – 0,1% брака. Найти вероятность того, что поступившая на сборку деталь – бракованная.
25
www.mitht.ru/e-library
Решение:
Пусть A {поступившая на сборку деталь – бракованная}, Hi {деталь изготовлена на i- ом автомате}, i 1,2,3. Бра-
кованная деталь может быть либо с первого автомата (собы-
тие AH1 ), либо со второго автомата (событие AH2 ), |
либо с |
||
третьего автомата (событие AH3 ). События H1, H2, H3 не- |
|||
совместны, |
|
|
|
P(H1) 0,1, |
P(H2 ) 0,4, |
P(H3) 0,5, |
(3.2) |
P(H1) P(H2 ) P(H3) 0,1 0,4 0,5 1. |
|
||
Поэтому из определения 3.3 следует, что H1, H2, H3 |
обра- |
||
зуют полную группу событий, и по формуле полной вероятности (3.1) имеем:
P(A) P(AH1) P(AH2) P(AH3) (3.3)
P(A H1)P(H1) P(A
H1)P(H1) P(A H2)P(H2) P(A
H2)P(H2) P(A H3)P(H3)
H3)P(H3)
Из условия примера
P(A H1) 0,002, P(A
H1) 0,002, P(A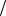 H2 ) 0,003, P(A
H2 ) 0,003, P(A H3 ) 0,001 (3.4)
H3 ) 0,001 (3.4)
Подставляя (3.2) и (3.4) в (3.3), получим
P(A) 0,002 0,1 0,003 0,4 0,001 0,5 0,0019.
Задачи для самостоятельного решения.
(В решении задач, помеченных звездочкой, используется формула полной вероятности.)
Задача 3.1.
Вероятность выигрыша по лотерейному билету равна 0,15. Какова вероятность того, что: а) из двух купленных билетов выигрыш выпадет на один из них? б) из трёх купленных билетов выигрыш выпадет на два из них? в) по крайней мере на один из четырёх купленных билетов выпадет выигрыш?
Задача 3.2.
Завод выпускает двигатели. Вероятность того, что выпущенный двигатель будет без дефектов, равна 0,99. Определить вероятность того, что: а) два подряд выпущенных двигателя
26
Пример 5.2.
Вероятность производства бракованной детали равна 0,006. Найти вероятность того, что в партии из 1000 деталей: а) не будет бракованных – событие A0 ; б) будет одна бракованная
– событие A1 ; в) будут две бракованные детали – событие
A2 .
Решение:
Здесь мы имеем дело с испытаниями Бернулли, где «успехом» является появление бракованной детали. При этом количество испытаний n 1000, вероятность «успеха» в одном
испытании |
p 0,006. |
Вычислим |
величину |
np 1000 0,006 6. Поскольку n 100 и |
np 10, то |
||
можно считать, что мы имеем дело с пуассоновской с.в. и
пользоваться формулой (5.4). На основании этой формулы |
|||||||
имеем: |
|
|
|
|
|
|
|
а) P(A ) |
60 |
|
e 6 e 6 ; |
||||
|
|
|
|
||||
0 |
0! |
|
|
||||
б) P(A ) |
6 |
e 6 6e 6 ; |
|||||
|
|
||||||
1 |
1! |
|
|
||||
в) P(A ) |
62 |
e 6 18e 6 . |
|||||
|
|||||||
2 |
2! |
|
|||||
Задачи для самостоятельного решения.
Задача 5.1.
При установившемся технологическом процессе станокавтомат производит 2 3 числа изделий первого сорта и 1
3 числа изделий первого сорта и 1 3 – второго сорта. Установить, что является более вероятным – получить 2 первосортных изделия среди 5 отобранных или
3 – второго сорта. Установить, что является более вероятным – получить 2 первосортных изделия среди 5 отобранных или
5первосортных среди 10 отобранных? Задача 5.2.
Что вероятнее выиграть у равносильного противника три партии из четырёх или пять из восьми?
43
www.mitht.ru/e-library

P( k) |
k |
e , 0, |
k 0,1,2, ,n |
(5.4) |
|||||
k! |
|||||||||
|
|
|
|
|
|
|
|
||
В таком случае ее ряд распределения есть: |
|||||||||
|
|
|
|
|
|
|
|
|
|
xi |
|
0 |
|
1 |
|
2 |
|
||
pi |
|
e |
|
e |
|
2 |
e |
|
|
|
|
|
|
|
|
2 |
|||
|
|
|
|
|
|
|
|
||
Математические ожидания и дисперсии для определенных выше случайных величин даны в следующей таблице:
Случайная |
Математическое |
Дисперсия |
Название распре- |
|||||
величина |
ожидание |
|
|
|
деления |
|||
n |
M n np |
D n npq |
биномиальное |
|||||
|
M |
D |
пуассоновское |
|||||
|
|
1 |
|
|
q |
|
геометрическое |
|
M p |
D p2 |
|||||||
|
|
|||||||
Пример 5.1.
Вероятность изготовления на автоматическом станке стандартной детали равна 0,9. Определить вероятность того, что из четырех наудачу взятых деталей две окажутся стандартными.
Решение:
Взяты 4 детали и произведены замеры каждой. Ясно, что мы имеем дело с 4 испытаниями Бернулли. При этом каждая из деталей может оказаться стандартной (успех) и нестандартной (неудача). Вероятность успеха p 0,9. Нас интересует
событие A2 {две детали из четырех стандартные}. Согласно (5.1) имеем
P2 P(A2 ) C42 (0,9)2 (0,1)2 4 3 0,81 0,01 0,0486. 1 2
42
будут без дефектов; б) из трёх подряд выпущенных двигателей только один будет дефектным.
Задача 3.3.
Вероятность из взятого случайным образом зерна получить колос, имеющий не менее 50 зёрен, равна 0,7 . Вычислить вероятность того, что из взятых наудачу 10 зёрен: а) вырастет хотя бы один колос, содержащий не менее 50 зёрен; б) ни один колос не будет содержать менее 50 зёрен.
Задача 3.4.
Из полной колоды карт (52 листа) вынимаются четыре карты. Найти вероятность того, что все эти четыре карты будут разных мастей, если а) карты вынимаются одновременно; б) каждая карта после вынимания возвращается в колоду.
Задача 3.5.
Вероятность того, что студент сдаст первый экзамен, равна 0,9; второй – 0,9; третий – 0,8. Найти вероятность того, что студентом будут сданы: а) только второй экзамен; б) только один экзамен; в) три экзамена; г) по крайней мере два экзамена; д) хотя бы один экзамен.
Задача 3.6.
При включении зажигания двигатель начнет работать с вероятностью 0,6. Найти вероятность того, что: а) двигатель начнет работать при третьем включении зажигания; б) для запуска двигателя придется включать зажигание не более трех раз.
Задача 3.7.
Студент разыскивает нужную ему формулу в трёх справочниках. Вероятность того, что формулы содержатся в 1-ом, 2- ом и 3-ем справочниках соответственно равны 0,6; 0,7 ; 0,8. Найти вероятность того, что формула содержится: а) только в одном справочнике; б) только в двух справочниках; в) во всех справочниках; г) не содержится ни в одном из них.
27
www.mitht.ru/e-library

Задача 3.8.* Имеются три одинаковые урны. В первой урне 2 белых и 1
чёрный шар, во второй – 3 белых и 1 чёрный, в третьей – 2 белых и 2 чёрных шара. Некто выбирает наугад одну урну и вынимает шар. Найти вероятность того, что шар белый.
Задача 3.9.* Из урны, содержащей 3 белых и 2 чёрных шара, переложи-
ли два вынутых наудачу шара в урну, содержащую 4 белых и 4 чёрных шара. Затем из второй урны взяли один шар. Найти вероятность того, что из второй урны вынут белый шар.
Задача 3.10.*
Студент пришёл на экзамен, зная m билетов из n. В каком случае вероятность взять несчастливый билет меньше, когда он берёт билет первым или вторым?
Задача 3.11.*
Вурну, содержащую два шара, опущен белый шар, после чего из неё наудачу извлечён один шар. Найти вероятность того, что извлечённый шар окажется белым, если равновероятны все возможные предположения о первоначальном составе шаров (по цвету).
Задача 3.12.
Вкруг радиуса R вписан квадрат. Чему равна вероятность того, что поставленные наудачу внутри круга две точки окажутся а) обе внутри квадрата; б) одна внутри квадрата, другая вне его; в) хотя бы одна внутри квадрата?
Задача 3.13.
Двое поочерёдно бросают монету. Выигрывает тот, у кого раньше появится герб. Определить вероятность выигрыша для каждого игрока.
28
Говорят, что случайная величина |
имеет геометриче- |
ское распределение, если вероятности |
событий { k }, |
k 1,2, задаются соотношениями |
|
P( k) (1 p)k 1 p |
(5.3) |
В этом случае ряд распределения случайной величины имеет вид:
xi |
1 |
2 |
3 |
|
n |
|
pi |
p |
qp |
q2 p |
|
qn 1 p |
|
где q 1 p .
Вероятностный смысл геометрической с.в. можно пояснить следующим образом. Пусть проводятся испытания Бернулли, но их количество заранее не ограничено. Пусть вероятность успеха в каждом отдельном испытании равна p (и, тем самым, вероятность неудачи равна q 1 p). Геометрическая с.в. – это номер испытания, в котором произойдет самый первый успех.
Еще одна важная дискретная с.в. получается, если рассматривать испытания Бернулли при n и p 0, причем так, что произведение np при этом стремится к некоторой постоянной величине . Для этой ситуации Пуассон доказал теорему, что вероятности Pn,k из формулы Бернулли
(5.1.) стремятся к пределу, равному k e . k!
На практике принято считать, что теорему Пуассона можно применять для испытаний Бернулли, где n и p таковы, что n 100, и при этом np 10. В качестве берется величина np.
Случайная величина имеет распределение Пуассона, если ее ряд распределения задается формулами
41
www.mitht.ru/e-library

V. Три широко распространенные дискретные с. в: биномиальная, пуассоновская и геометрическая.
Многие ситуации, возникающие в теории вероятностей, могут быть описаны с помощью схемы, называемой схемой Бернулли.
Пусть проводится n одинаковых независимых случайных экспериментов (или, по-другому, испытаний). Часто такая серия экспериментов называется испытаниями Бернулли. Можно также считать, что один и тот же эксперимент повторяется независимо n раз. Мы интересуемся появлением в каждом эксперименте одного и того же события, которое принято условно называть «успехом» (а противоположное событие принято называть «неудачей»). Пусть вероятность «успеха» в одном испытании равна p . Вероятность того, что в серии из n испытаний Бернулли произойдет ровно k успехов (0 k n) вычисляется по формуле:
P |
Ck pk (1 p)n k , |
(5.1) |
n,k |
n |
|
называемой формулой Бернулли.
Понятно, что количество успехов в n испытаниях Бернулли является дискретной случайной величиной. Эта с.в. называется бернуллиевской или биномиальной, и обозначается обычно n .
Из формулы Бернулли (5.1) следует, что
P( n k) Cnk pk (1 p)n k . |
(5.2) |
Таким образом, ряд распределения случайной величины n
имеет вид:
xi |
0 |
1 |
|
|
|
|
2 |
|
|
n |
pi |
(1 p)n |
np(1 p)n 1 |
|
n(n 1) |
p |
2 |
(1 p) |
n 2 |
|
pn |
|
|
|
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
|
|
|
40 |
|
|
|
|
|
|
|
IV. Дискретная случайная величина. Ряд распределения. Числовые характеристики и функция распределения дискретной случайной величины.
Напомним, что величина y называется функцией действительной переменной x, если каждому значению x, взятому из некоторого множества X , соответствует единственное значение y из множества Y .
Это определение может быть расширено на те случаи, когда независимая переменная не является действительным числом. Например, периметр треугольника является функцией, определенной на множестве треугольников; модуль a
вектора a является функцией, определенной на множестве векторов и т.д.
Определение 4.1. Числовая функция, определенная на пространстве элементарных событий, называется случайной величиной (сокращенно с. в.).
Можно сказать по-другому: Случайная величина – это такая числовая величина, точное значение которой становится известным только после проведения опыта.
Очень много величин, с которыми приходится иметь дело, являются случайными. Скажем, количество пассажиров в вагоне метро, время между двумя последовательно поступившими телефонными звонками, рост (а также вес, размер обуви, и т.д.) наугад выбранного человека, время службы электрической лампочки и многое-многое другое.
Пример 4.1.
Пусть одновременно один раз бросаются две монеты достоинством 1 руб. и 2 руб. Выпишем элементарные события:1 (Г,Г), 2(Г,2), 3 (1,Г), 4 (1,2). На пространстве элементарных событий могут быть определены несколько случайных величин. Пусть 1 – число выпадений герба, 2 –
29
www.mitht.ru/e-library

сумма выпавших цифр, 3 – число выпавших четных цифр. Тогда 1 2 (при 1), 1 1 (при 2 и 3 ), 1 0 (при 4 );
2 0 (при 1), 2 2 (при 2 ), 2 1 (при 3 ),
2 3 (при 4 );
3 0 (при 1 и 3 ), 3 1 (при 2 и 4 ).
Представим значения случайных величин 1 , |
2 и |
3 при |
||||
различных элементарных событиях в виде таблицы 1: |
|
|||||
|
|
|
|
|
|
|
|
1 |
2 |
3 |
|
|
4 |
1 |
2 |
1 |
1 |
|
|
0 |
2 |
0 |
2 |
1 |
|
|
3 |
3 |
0 |
1 |
0 |
|
|
1 |
Определение 4.2. Случайная величина, возможные значения которой образуют конечное или бесконечное множество, состоящее из изолированных друг от друга числовых значений, называется дискретной.
Пусть x1,x2 ,x3, , – значения, которые может прини-
мать случайная величина . Одно и то же значение xj мо-
жет соответствовать нескольким элементарным событиям. Совокупность всех этих элементарных событий образует составное событие, состоящее в том, что xj . Это событие
обозначается xj или xj , а вероятность этого со-
бытия обозначается p( xj ).
Определение 4.3. Система равенств p( xj ) pj , j 1,2, ,
где pj |
1, определяет распределение (ряд распределения) |
j |
|
случайной величины . Обычно ряд распределения выписывают в виде таблицы, состоящей из двух строк. В верхней
30
та и 10% изделий второго сорта. – число изделий первого сорта среди трех изделий, отобранных наугад из партии.
Найти P( 3), P(1 2).
Задача 4.16.
По данным функциям распределения восстановить ряды распределений в случаях
0, x 1,
а) F(x) 1 3, 1 x 1 2,
1, x 1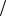 2.
2.
0, x 0,5,
2 3, 0,5 x 0,5, в) F(x)
5 6,0,5 x 1,5,
1, x 1,5.
0, x 2,
б) F(x) 1 2, 2 x 0,
1, x 0.
0, x 4,
0,25, 4 x 3,
г) F(x) 0,5, 3 x 2,
0,75, 2 x 1,
1, x 1.
Задача 4.17.
Могут ли следующие функции быть функциями распределения? Если нет, то какие из свойств F(x) нарушены?
0, x 1,
а) F(x) 1, 1 x 0,2, x 0.
0, x 1, в) F(x)
1, x 1.
0, x 1,
д) F(x) 1 2, 1 x 2,
1, x 2.
1, x 0, б) F(x)
1, x 0.
1, x 1,
г) F(x) 2 3,1 x 2,0, x 2.
0, x 1,
е) F(x) 4 5, 1 x 3,
1, x 3.
39
www.mitht.ru/e-library
