
теория вероятности
.pdfИздание учебное
Рыкова Любовь Викторовна Рубин Александр Григорьевич Ожерелкова Лилия Мухарамовна
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Учебно-методическое пособие
Подписано в печать |
Формат 60x84/16. Бумага писчая. |
Отпечатано на ризографе. |
Уч. изд. листов 2,08. Тираж 100 экз. |
Заказ №…………. |
|
Лицензия на издательскую деятельность ИД № 03507 (рег. № 003792) код 221
Московская государственная академия тонкой химической технологии им М.В. Ломоносова
Издательско-полиграфический центр 119571 Москва, пр. Вернадского, 86.
68
Федеральное агентство по образованию
Московская государственная академия тонкой химической технологии им. М.В. Ломоносова
Кафедра высшей и прикладной математики
Рыкова Л.В., Рубин А.Г., Ожерелкова Л.М.
ТЕОРИЯ
ВЕРОЯТНОСТЕЙ
Учебно-методическое пособие
Москва 2008
1
www.mitht.ru/e-library

УДК 519.21 ББК 22.171
Рецензенты: ст. преп. Соснин М.Л. (МИТХТ, каф. ВиПМ)
к.ф.-м.н., доцент Краснослободцев А.В. (РУДН)
Рыкова Л.В., Рубин А.Г., Ожерелкова Л.М.
Теория вероятностей
Учебно-методическое пособие М., МИТХТ им. М.В. Ломоносова, 2008 – 66 с.
Утверждено Библиотечно-издательской комиссией МИТХТ им. М.В. Ломоносова в качестве учебно-методи- ческого пособия. Поз._ _ /2008.
Данное учебно-методическое пособие является дополнением к существующим учебникам и задачникам по теории вероятностей и отражает содержание читаемой для студентов 2 курса учебной дисциплины «Теория вероятностей и математическая статистика» для всех направлений бакалавриата и всех специальностей дневной и вечерней форм обучения. Оно содержит необходимые теоретические сведения, типовые задачи с решениями, а также достаточное количество упражнений для самостоятельной работы студентов.
Издание 3-е.
© МИТХТ им. М.В. Ломоносова, 2003
2 |
67 |
www.mitht.ru/e-library

6.9. k 1; M 1  2; D 3;
2; D 3;
P(  4 0)
4 0) 
 2
2 2; P(
2; P(  6) 1
6) 1 2.
2.
6.10. k 4 3; M 2
3; M 2 9; P(
9; P(  4) 1
4) 1 3; P(
3; P(  3) 1.
3) 1.
6.12. а) не может, т.к. sin x 0 при x  2,0 ; б) не может,
2,0 ; б) не может,
|
2 |
|
dx |
|
т.к. |
xdx 3 |
2; в) не может, т.к. |
|
; г) не может, |
1 x2 |
||||
|
1 |
|
|
|
т.к. |
f (x) 0 |
при x 0. |
|
|
7.1. а) M 2; D 1 3; б) M 0; D 1
3; б) M 0; D 1 3;
3;
в) M 3 2; D 27
2; D 27 4.
4.
7.2. M 1 2; D 1
2; D 1 4; P( 1
4; P( 1 2) 1 e 1 ;
2) 1 e 1 ;
P( 1 1) 1 e 2 ; P( 3) e 6 .
7.3. B 1 ; F(x) |
1 |
|
arctgx |
1 |
; |
P( 1 1) 1 2; |
|
|
|
||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||
P( |
|
3) 5 6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
7.4. A 1 ; F(x) |
2 |
arctgex ; P(0 2) |
2 |
arctg e2 |
|
1 |
; |
||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||
P( 1) |
1 |
arctg e . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
4 |
|
2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
7.5. Mv |
2 (h );Dv |
|
|
|
|
h |
|
. |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||
7.6. M 3,868; D 3,841; |
P( 4) 0,541. |
|
|
|
|||||||||||||||||||||
7.7. а) 0,1587; б) 0,3821; в) 0,9972; г) 0,8185. |
|
|
|
||||||||||||||||||||||
7.8. . а) |
1; б) |
0,6; в) 2,1; г) 1,22. |
|
|
|
|
|
|
|||||||||||||||||
7.9. M |
1; |
D 3; P( 2 2) 0,6772; |
|
|
|
||||||||||||||||||||
P( 1) |
0,1251. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
66
Содержание:
I. Пространство элементарных событий. Определение вероятностей событий в простых случаях…………………….......
………………………………………………………………......4 II. Вычисление вероятностей событий с помощью формул комбинаторного анализа………………………………………
………………………………………………………………….12
III. Условная вероятность. Теоремы сложения и умножения вероятностей. Формула полной вероятности………………..
………………………………………………………………….21
IV.Дискретная случайная величина. Ряд распределения. Числовые характеристики и функция распределения дискретной случайной величины………………………………………
………………………………………………………………….29
V. Три широко распространенные дискретные с. в: биномиальная, пуассоновская и геометрическая…………………….
…………………………………………………………………40
VI. Непрерывная случайная величина и ее характеристики.
…………………………………………………………………46
VII. Примеры непрерывных случайных величин…………....
…………………………………………………………………56
Приложение…………………………………………………..62 Ответы………………………………………………………...63
3
www.mitht.ru/e-library

I. Пространство элементарных событий. Определение вероятностей событий в простых случаях.
В теории вероятностей одним из основных понятий является понятие случайного эксперимента (или случайного опыта). Под случайным опытом в теории вероятностей понимается такой опыт, конкретный исход которого не известен до его проведения, но заранее известно множество всех возможных исходов.
Всякий результат опыта будем называть событием. События бывают разложимые (или составные) и неразложимые. Каждый неразложимый исход опыта называется элементарным событием и обычно обозначается i ,i 1,2,3,
Множество всех элементарных событий, соответствующих данному опыту, называется пространством элементарных событий и обозначается i , где область изме-
нения индекса i зависит от конкретного опыта.
Событием является любое подмножество A пространства элементарных событий. Событие A наступает тогда, когда в результате опыта происходит одно из элементарных событий, входящих в A.
Пример 1.1.
Из трех цифр 2, 5, 7 наудачу берутся две цифры, и составляется число.
1)Выписать все элементарные события этого опыта. Составить из элементарных событий события:
2)A={полученное число содержит цифру 5};
3)B ={число содержит только нечетные цифры};
4)C={полученное число четно}.
Решение:
1) Пространство элементарных событий состоит из следующих элементарных событий:
1 2 5 , 2 2 7 , 3 5 2 , 4
|
|
|
|
|
|
|
|
m 1 |
m 3 |
6 m |
|
|
|
|
|
|
||||||||||
5.4. 0,64. |
|
|
|
|
5.5. C6 |
|
|
|
|
|
|
|
. |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
4 |
4 |
|
|
|
|
|
|
|
|
|||||||
5.6. 0,26; 14. |
|
|
|
5.7. 0,07. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 |
1 |
2 6 |
|
4 |
3 |
|
|
1 3 |
6 |
3 |
|
6 |
6 |
|
|
|
|
|||||||||
5.8. а) C6 |
|
|
|
|
|
; б) C6 |
|
|
|
|
|
|
|
; |
|
|
. |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
7 7 |
|
|
7 7 |
|
|
7 |
|
|
|
|
|||||||||||||||
5.9. 0,3 5 11,75. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
5.10. а) 0,8 6 1,2 0,8 5 ; б) 0,8 6 ; в) |
1 0,8 6 . |
|
|
|
||||||||||||||||||||||
5.11. Cnm 3m (1 3 )n m . |
|
5.12. P( 8) |
88 |
e 8 . |
|
|
|
|||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8! |
|
|
|
|
|
5.13. P( m) Cm |
(0,02)m (0,98)100 m и P( m) |
28 |
|
e 2 . |
||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m! |
|
|
5.14. 1 e 0,516 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
6.1. A 1 3; |
M 4 9; D 13 162; |
|
|
|
|
|
|
|||||||||||||||||||
P( 1 6 0) 23
6 0) 23 108; P( 1
108; P( 1 2) 7
2) 7 12.
12.
6.2. A 
 2 ; P(
2 ; P(  6)
6) 
 2
2 2; P( 1) 0.
2; P( 1) 0.
6.3. A 1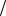 2;B 1
2;B 1 4; C 1; P( 4 0) 23
4; C 1; P( 4 0) 23 32;
32;
P( 2) 1 8; P( 1
8; P( 1 2) 3
2) 3 8.
8.
6.4. A 5 16; M 91
16; M 91 32; D ; P( 1 5) 24
32; D ; P( 1 5) 24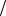 25;
25;
P( 1 1) 0; P( 0) 0.
6.5. k 40 81; M 329
81; M 329 162;D 0,489;
162;D 0,489;
P( 5 2 2) 20
2 2) 20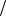 81; P( 0) 1; P( 1) 0.
81; P( 0) 1; P( 1) 0.
6.6. k 2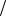 3; M 1; D 1
3; M 1; D 1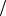 2; P( 1) 4
2; P( 1) 4 9;
9;
P(3 2 3) 1
2 3) 1 4.
4.
6.7. k 23 12; M 43
12; M 43 24; D ; P( 1) 23
24; D ; P( 1) 23 24;
24;
P( 0) 1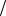 24.
24.
6.8. k 3; M 1 4; D 3
4; D 3 80; P(0 1
80; P(0 1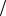 2) 7
2) 7 8;
8;
P( 1 4) 27
4) 27 64.
64.
65
www.mitht.ru/e-library

3.2. а) (0,99)2 ; б) 0,03 (0,99)2 .
3.3. а) 1 (0,3)10 ; б) |
(0,7)10 . 3.4. а) 0,106; б) 0,094. |
|
3.5. а) 0,018; б) 0,044; в) 0,648; г) 0,954; д) 0,998. |
||
3.6. а) 0,096; б) 0,936. |
||
3.7. а) 0,188; б) 0,452; в) 0,336; г) 0,024. |
||
3.8. 23 36. |
|
3.9. 0,52. |
3.10. Вероятность одинакова и равна (n-m) n . |
||
3.11. 2 3. |
3.12. а) (2 )2 ; б) 4( -2) 2 ; в) (4 -4) 2 . |
|
3.13. 2 3 и 1 3. |
|
|
4.1. M 1 3; D 8
3; D 8 9; 0; 1
9; 0; 1 3; 2
3; 2 3; 0.
3; 0.
4.2. M 5 7; D 69
7; D 69 98; 1
98; 1 7; 5
7; 5 7; 2
7; 2 7; 0. 4.3. M 5
7; 0. 4.3. M 5 2; D 13
2; D 13 4; 1
4; 1 2; 0.
2; 0.
4.4. M 1 1;D 1 1 2;M 2 2;D 2 2; 3
2;M 2 2;D 2 2; 3 4;1
4;1 4; 1
4; 1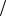 4;3
4;3 4;0 4.5. M 1 1;D 1 1
4;0 4.5. M 1 1;D 1 1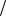 2;M 2 1
2;M 2 1 2;D 2 1
2;D 2 1 4; 1
4; 1 4; 0;1
4; 0;1 4; 1
4; 1 2. 4.6. M 1
2. 4.6. M 1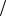 2; D 1
2; D 1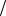 4; 0; 0; 1
4; 0; 0; 1 2.
2.
4.7. M 1; D 1 2; 1
2; 1 4; 1
4; 1 4; 3
4; 3 4.
4.
4.8. M 4 3; D 4
3; D 4 9; 0; 1
9; 0; 1 9.
9.
4.9. M 1; D 1 2; 0; 0; 3
2; 0; 0; 3 4.
4.
4.10. |
M 19 90; |
D 1529 8100; 1 90; |
4 5. |
|
4.11. |
M 17 18; |
D 161 324; 0; 2 9. |
|
|
4.12. P( 2) 3 4; P( 3) 1 8. |
|
|||
4.13. M 2 3; D 4 9; 0; 5 9. |
|
|||
4.14. |
M 1,7; |
D 0,25; 0,02; 0. |
|
|
4.15. M 2,7; |
D 0,27; 1; 0,027 . |
|
||
4.17. а) нет; б) нет; в) да; г) нет; д) да; е) нет. |
||||
5.1. 2 из 5. |
|
5.2. 3 из 4. |
5.3. 0,784. |
|
64
4 5 7 , 5 7 2 , 6 7 5 ;
2) A 1, 3, 4 , 6 ; 3) B 4 , 6 ; 4) C 3, 5 .
Определение 1.1. Суммой C A B (или C A B) двух событий A и B называется такое событие, которое состоит из элементарных событий, входящих хотя бы в одно из событий A или B .
Определение 1.2. Произведением D A B (или D A B) двух событий A и B называется такое событие, которое состоит из элементарных событий, входящих одновременно и в A, и в B .
Любое событие, связанное с данным опытом, может быть описано с помощью суммы элементарных событий, составляющих данное событие. Так, в примере 1.1:
A 1 3 4 6 , B 4 6 , C 3 5 .
Очень важно научиться замечать в тексте задачи филологические, языковые признаки того, идет ли речь о сумме событий или о произведении. Для суммы событий такими признаками являются языковые конструкции «или», «хотя бы одно из событий», «по крайней мере одно из событий», а для произведения – «и», «одновременно все события», «сразу все события».
Определение 1.3. Событие называется достоверным, если оно обязательно произойдёт в результате опыта.
Определение 1.4. Событие, которое в результате опыта произойти не может, называется невозможным событием и обозначается .
Определение 1.5. Событие A называется противоположным
событию A, если A A и A A .
Можно сказать и по-другому: событием, противопо-
ложным событию A, называется такое событие A , которое происходит тогда и только тогда, когда не происходит событие A.
5
www.mitht.ru/e-library

Очевидно, является достоверным событием. Событие A B означает, что, по крайней мере, одно из событий A или B произошло. Событие A B означает, что произошли оба события A и B .
Определение 1.6. События A и B называются несовместными, если A B .
Ясно, что:
1)несовместные события не могут произойти одновременно;
2)A и A несовместны;
3)все элементарные события попарно несовместны.
Пример 1.2.
В условиях примера 1.1. найти:
1)события A , B , C ;
2)события A C, C B, A B, A C, B C. Решение:
1) A {число не содержит цифру 5}={ 2 , 5 };
B={содержит цифру 2}={ 1, 2 , 3, 5 };
C={полученное число нечетно}={ 1, 2, 4, 6 };
2) A C={число либо содержит цифру 5, либо четно, либо и то, и другое}={ 1, 3, 4, 5, 6 };
C B={число либо содержит только нечетные цифры, либо
четно}={ 3, 4 , 5 , 6 };
A B ={число содержит только нечетные цифры, одна из них 5}={ 4, 6 };
A C ={число содержит цифру 5 и четно}={ 3};
B C ={число четно и содержит только нечетные циф-
ры}= .
События B и C – несовместны.
Определение 1.7. Класс подмножеств множества называется алгеброй событий F , если он вместе с каждым событи-
6
Ответы.
1.1. 1 3. |
|
|
|
1.2. а) 3 28; б) 1 7; в) 1 28; г) 0; д) 3 14. |
|||||||||||||||||
1.3. а) 1 60; б) 1 5; в) 3 5; г) 1 20; д) 2 5. |
|
|
|
|
|||||||||||||||||
1.4. а) 1 9; б) 1 50; в) 1 90. |
|
|
|
|
|
|
|
|
|
||||||||||||
1.5. а) 0,3024; б) 0,01; в) 0,95 ; г) 1 32. |
|
|
|
|
|||||||||||||||||
1.6. а) 5 18; б) 5 6; в) 5 36. |
|
|
1.7. а) 14 63; б) 49 63. |
||||||||||||||||||
1.8. а) 2 9; б) 4 9; в) 5 9. |
|
|
|
1.9. 0,061 |
1.10. 0,68. |
||||||||||||||||
1.11. а) 1 4; б) 1 9; в) 1 36. |
|
|
2.1. 300 3553. |
|
|||||||||||||||||
2.2. а) 7 24; б) 7 40. |
|
|
|
|
2.3. а) 1 35; б) 18 35. |
||||||||||||||||
2.4. P(A) C42 C4824 |
C5226 ; P(B) 2C4826 |
C5226 ; P(C) 8C4825 C5226 ; |
|||||||||||||||||||
|
P(D) 2C1339 |
C5226 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2.5. P(A) C10 |
C10 |
; P(B) 0; P(C) C6 |
C2 |
C8 ; |
|||||||||||||||||
|
|
|
|
|
|
|
40 |
50 |
|
|
|
|
|
|
|
40 |
10 |
50 |
|||
|
P(D) 1 (C1050 ) 1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2.6. а) 81 8! 109 ; б) 9! 109 . |
|
|
|
|
|
|
|
|
|
|
|||||||||||
2.7. а) 57 115; б) 229 230; в) 2 23. |
2.8. (C1020 )2 C4020 . |
||||||||||||||||||||
2.9. а) 0,504; б) 0,001; в) 0,496; |
2.10. |
44 45 |
|||||||||||||||||||
2.11. а) 5 6; б) 1 30; в) 1 6. |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
1 |
|
0,265 10 5 ; б) |
|
C4 |
C1 |
|
|
|
|
|
||||||
2.12. а) |
|
|
|
5 |
31 |
0,41 10 3 |
; в) |
||||||||||||||
|
|
|
|
|
C365 |
|
|
|
|
|
|
C365 |
|
|
|
|
|
||||
|
C3 |
C2 |
0,012; г) |
C5 |
0,45; |
|
|
|
|
|
|
|
|||||||||
|
5 |
31 |
|
31 |
|
|
|
|
|
|
|
||||||||||
C365 |
C365 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2.13. а) |
C6 |
0,72 10 3 |
|
C6 |
|
|
|
|
C3 C3 |
||||||||||||
8 |
|
; б) |
|
12 |
|
0,238; в) |
|
5 |
7 |
0,009; |
|||||||||||
C206 |
C206 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C206 |
|||||||
|
|
C2 C2 C2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
г) |
|
5 |
|
7 |
|
8 |
0,15; |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
C206
3.1. а) 0,255; б) 0,057375; в) 1 (0,85)4 . 63
www.mitht.ru/e-library

Приложение.
|
|
|
|
|
|
|
1 |
|
x |
|
t2 |
|
|
|||
|
|
|
|
|
|
|
|
e |
|
|
|
|
||||
|
Значения функции Лапласа Ф(x) |
|
2 dt |
|
|
|||||||||||
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
2 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||
x |
|
|
|
|
Cотые доли x |
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
|
7 |
8 |
9 |
|||
0,0 |
0,0000 |
0,0040 |
0,0079 |
0,0120 |
0,0159 |
0,0199 |
0,0239 |
|
0,0279 |
0,0319 |
0,0359 |
|||||
0,1 |
0,0398 |
0,0438 |
0,0478 |
0,0517 |
0,0557 |
0,0596 |
0,0636 |
|
0,0675 |
0,0714 |
0,0754 |
|||||
0,2 |
0,0792 |
0,0832 |
0,0871 |
0,0910 |
0,0948 |
0,0987 |
0,1026 |
|
0,1064 |
0,1103 |
0,1141 |
|||||
0,3 |
0,1179 |
0,1217 |
0,1255 |
0,1293 |
0,1331 |
0,1368 |
0,1406 |
|
0,1443 |
0,1480 |
0,1517 |
|||||
0,4 |
0,1554 |
0,1591 |
0,1628 |
0,1664 |
0,1700 |
0,1336 |
0,1772 |
|
0,1808 |
0,1844 |
0,1879 |
|||||
0,5 |
0,1915 |
0,1950 |
0,1985 |
0,2019 |
0,2054 |
0,2088 |
0,2123 |
|
0,2157 |
0,2190 |
0,2224 |
|||||
0,6 |
0,2258 |
0,2291 |
0,2324 |
0,2357 |
0,2389 |
0,2422 |
0,2454 |
|
0,2486 |
0,2518 |
0,2549 |
|||||
0,7 |
0,2580 |
0,2612 |
0,2642 |
0,2673 |
0,2704 |
0,2734 |
0,2764 |
|
0,2794 |
0,2823 |
0,2852 |
|||||
0,8 |
0,2881 |
0,2910 |
0,2939 |
0,2967 |
0,2996 |
0,3023 |
0,3051 |
|
0,3079 |
0,3106 |
0,3133 |
|||||
0,9 |
0,3159 |
0,3186 |
0,3212 |
0,3238 |
0,3264 |
0,3289 |
0,3315 |
|
0,3340 |
0,3365 |
0,3389 |
|||||
1,0 |
0,3413 |
0,3438 |
0,3461 |
0,3485 |
0,3508 |
0,3531 |
0,3554 |
|
0,3577 |
0,3599 |
0,3621 |
|||||
1,1 |
0,3643 |
0,3665 |
0,3686 |
0,3708 |
0,3729 |
0,3749 |
0,3770 |
|
0,3800 |
0,3810 |
0,3830 |
|||||
1,2 |
0,3849 |
0,3869 |
0,3888 |
0,3907 |
0,3925 |
0,3944 |
0,3962 |
|
0,3980 |
0,3997 |
0,4015 |
|||||
1,3 |
0,4032 |
0,4049 |
0,4066 |
0,4082 |
0,4099 |
0,4115 |
0,4131 |
|
0,4147 |
0,4162 |
0,4177 |
|||||
1,4 |
0,4192 |
0,4207 |
0,4222 |
0,4236 |
0,4251 |
0,4265 |
0,4279 |
|
0,4292 |
0,4306 |
0,4319 |
|||||
1,5 |
0,4332 |
0,4345 |
0,4357 |
0,4370 |
0,4382 |
0,4394 |
0,4406 |
|
0,4418 |
0,4430 |
0,4441 |
|||||
1,6 |
0,4452 |
0,4463 |
0,4474 |
0,4485 |
0,4495 |
0,4505 |
0,4515 |
|
0,4525 |
0,4535 |
0,4545 |
|||||
1,7 |
0,4554 |
0,4564 |
0,4573 |
0,4582 |
0,4591 |
0,4599 |
0,4608 |
|
0,4616 |
0,4625 |
0,4633 |
|||||
1,8 |
0,4641 |
0,4649 |
0,4656 |
04664 |
0,4671 |
0,4678 |
0,4686 |
|
0,4693 |
0,4700 |
0,4706 |
|||||
1,9 |
0,4713 |
0,4719 |
0,4726 |
0,4732 |
0,4738 |
0,4744 |
0,4750 |
|
0,4756 |
0,4762 |
0,4767 |
|||||
2,0 |
0,4773 |
0,4778 |
0,4783 |
0,4788 |
0,4793 |
0,4798 |
0,4803 |
|
0,4808 |
0,4812 |
0,4817 |
|||||
2,1 |
0,4821 |
0,4826 |
0,4830 |
0,4834 |
0,4838 |
0,4842 |
0,4846 |
|
0,4850 |
0,4854 |
0,4857 |
|||||
2,2 |
0,4861 |
0,4865 |
0,4868 |
0,4871 |
0,4875 |
0,4878 |
0,4881 |
|
0,4884 |
0,4887 |
0,4890 |
|||||
2,3 |
0,4893 |
0,4896 |
0,4898 |
0,4901 |
0,4904 |
0,4906 |
0,4909 |
|
0,4911 |
0,4913 |
0,4916 |
|||||
2,4 |
0,4918 |
0,4920 |
0,4922 |
0,4925 |
0,4927 |
0,4929 |
0,4931 |
|
0,4932 |
0,4934 |
0,4936 |
|||||
2,5 |
0,4938 |
0,4940 |
0,4941 |
0,4943 |
0,4945 |
0,4946 |
0,4948 |
|
0,4949 |
0,4951 |
0,4952 |
|||||
2,6 |
0,4953 |
0,4955 |
0,4956 |
0,4957 |
0,4959 |
0,4960 |
0,4961 |
|
0,4962 |
0,4963 |
0,4964 |
|||||
2,7 |
0,4965 |
0,4966 |
0,4967 |
0,4968 |
0,4969 |
0,4970 |
0,4971 |
|
0,4972 |
0,4973 |
0,4974 |
|||||
2,8 |
0,4974 |
0,4975 |
0,4976 |
0,4977 |
0,4977 |
0,4978 |
0,4979 |
|
0,4980 |
0,4980 |
0,4981 |
|||||
2,9 |
0,4981 |
0,4982 |
0,4983 |
0,4983 |
0,4984 |
0,4984 |
0,4985 |
|
0,4985 |
0,4986 |
0,4986 |
|||||
3,0 |
0,4987 |
0,4987 |
0,4987 |
0,4987 |
0,4988 |
0,4989 |
0,4989 |
|
0,4989 |
0,4990 |
0,4990 |
|||||
3,1 |
0,4990 |
0,4990 |
0,4991 |
0,4991 |
0,4992 |
0,4992 |
0,4992 |
|
0,4992 |
0,4993 |
0,4993 |
|||||
3,2 |
0,4993 |
0,4993 |
0,4994 |
0,4994 |
0,4994 |
0,4994 |
0,4994 |
|
0,4995 |
0,4995 |
0,4995 |
|||||
3,3 |
0,4995 |
0,4995 |
0,4996 |
0,4996 |
0,4996 |
0,4996 |
0,4996 |
|
0,4996 |
0,4996 |
0,4997 |
|||||
3,4 |
0,4997 |
0,4997 |
0,4997 |
0,4997 |
0,4997 |
0,4997 |
0,4997 |
|
0,4997 |
0,4998 |
0,4998 |
|||||
3,5 |
0,4998 |
0,4998 |
0,4998 |
0,4998 |
0,4998 |
0,4998 |
0,4998 |
|
0,4998 |
0,4998 |
0,4998 |
|||||
3,6 |
0,4998 |
0,4998 |
0,4998 |
0,4999 |
0,4999 |
0,4999 |
0,4999 |
|
0,4999 |
0,4999 |
0,4999 |
|||||
3,7 |
0,4999 |
0,4999 |
0,4999 |
0,49990 |
0,4999 |
0,4999 |
0,4999 |
|
0,4999 |
0,4999 |
0,4999 |
|||||
3,8 |
0,4999 |
0,4999 |
0,4999 |
0,4999 |
0,4999 |
0,4999 |
0,4999 |
|
0,4999 |
0,4999 |
0,4999 |
|||||
3,9 |
0,4999 |
0,4999 |
0,4999 |
0,4999 |
0,4999 |
0,4999 |
0,4999 |
|
0,4999 |
0,4999 |
0,4999 |
|||||
4,0 |
0,4999 |
0,4999 |
0,4999 |
0,4999 |
0,4999 |
0,4999 |
0,4999 |
|
0,4999 |
0,4999 |
0,4999 |
|||||
|
|
|
|
|
62 |
|
|
|
|
|
|
|
|
|
|
|
ем A содержит и противоположное событие A , а с каждой парой событий A и B содержит события A B, A B .
Во многих вероятностных экспериментах приходится рассматривать бесконечные последовательности событий и операции над ними. При этом:
1) событие Ak означает осуществление хотя бы одного из
k 1
событий Ak , k 1,2, .
2) событие Ak означает осуществление каждого из собы-
k 1
тий Ak , k 1,2, .
Определение I.8. Алгебра событий F называется - алгеброй событий (борелевской алгеброй), если из того, что
Ak F, k 1,2, , следует Ak F , Ak F .
k 1 k 1
В дальнейшем рассматриваются только такие эксперименты, в которых случайные события образуют - алгебру.
Определение I.9. Числовая функция P , определённая на - алгебре событий F , называется вероятностью, если выполнены следующие условия:
1)P(A) 0 для любого A F ;
2)P( ) 1;
3) если A1,A2, Ak , – несовместны, тоP( Ak ) P(Ak ).
k 1 k 1
Рассмотрим один очень важный частный случай вычисления вероятностей, называемый классической схемой.
Классическая схема применяется в ситуации, когда количество элементарных событий конечно, причем все они равноценны, т.е. ни одно из элементарных событий ничем не «лучше» и не «хуже» другого. Тогда ясно, что вероятность
7
www.mitht.ru/e-library

каждого элементарного события равна 1 N , где N – количество элементарных событий в , а вероятность события A, состоящего из m элементарных событий, равна m
N , где N – количество элементарных событий в , а вероятность события A, состоящего из m элементарных событий, равна m N . Обычно для краткости вместо «элементарное событие» говорят «исход», а те исходы (т.е. элементарные события), при которых происходит интересующее нас событие A, называют благоприятными для события A или просто благоприятными.
N . Обычно для краткости вместо «элементарное событие» говорят «исход», а те исходы (т.е. элементарные события), при которых происходит интересующее нас событие A, называют благоприятными для события A или просто благоприятными.
Тогда можно сказать, что в классической схеме вероятность события равна отношению количества благоприятных исходов к количеству всех возможных исходов:
P(A) m N , |
(1.1) |
где m – количество благоприятных для события A исходов, N – общее количество исходов.
При этом возможность или невозможность применения классической схемы при решении конкретной задачи устанавливается из здравого смысла. Например, если из колоды карт, содержащей 32 карты, наугад вытаскивается одна, то ясно, что здесь классическая схема применима, если карта действительно вытаскивается «наугад», т.е. нет никакого жульничества (карты не помечены, нет возможности подсматривать т. д.).
Пример 1.3.
В условиях примеров 1.1. и 1.2., считая все элементарные
события |
равновероятными, |
вычислить: |
||
Pj P( j ), |
j 1,2, ,6, P(A), P(B), |
P(C), P( |
|
), |
A |
||||
P(A C), P(A C), P(B C). |
|
|
|
|
Решение. |
|
|
|
|
В этих примерах N 6. Следовательно, Pj |
P( j ) 1 6. Из |
|||
(1.1) и определения соответствующих событий получаем:
P(A) 4 6 2
6 2 3; P(B) 2
3; P(B) 2 6 1
6 1 3; P(C) 2
3; P(C) 2 6 1
6 1 3;
3;
8
0, |
|
|
v 0, |
|
||||
|
|
|
|
|
|
|
|
|
f (v) 4h3 |
|
|
2 |
|
h2v2 |
|
||
|
|
|
|
v |
|
e |
, v 0, |
h 0 |
|
|
|
|
|||||
|
|
|||||||
|
|
|
|
|
|
|
||
Задача 7.6.
Число - частиц, достигающих счетчика в некотором опыте, является случайной величиной , распределенной по сле-
дующему закону: |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
0 |
|
1 |
2 |
|
|
3 |
4 |
5 |
|
|
|
|
|
|
p |
|
0,021 |
|
0,081 |
0,156 |
|
0,201 |
0,195 |
0,151 |
|
|
|
|
|
||
продолжение таблицы |
|
|
|
|
|
|
|
|
|
|||||||
|
|
6 |
|
7 |
8 |
|
|
9 |
10 |
|
|
|
|
|
|
|
p |
|
0,097 |
0,054 |
0,026 |
0,011 |
0,007 |
|
|
|
|
|
|
||||
Найти M , |
D , P( 4). |
|
|
|
|
|
|
|
|
|
||||||
|
Задача 7.7. |
|
|
|
|
|
|
|
|
|
|
|
||||
Для с. в. ~ N(2;1) найти вероятности: |
|
|
|
|
|
|
||||||||||
а) |
P( 1); б) P( 2,3), в) |
P( 1 5), г) P(0 3). |
||||||||||||||
|
Задача 7.8. |
|
|
|
|
|
|
|
|
|
|
|
||||
Для с. в. ~ N( 1;2) найти число x из условий: |
|
|
|
|
||||||||||||
а) |
P( x) 0,5; б) P(x ) 0,3, в) P(x 0) 0,4, |
|||||||||||||||
г) P( 2 x) P(0 1). |
|
|
|
|
|
|
|
|||||||||
|
Задача 7.9. |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
(x 1)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Для с. в. с плотностью распределения |
f (x) |
|
|
|
e 6 |
|||||||||||
|
|
|
||||||||||||||
6 |
||||||||||||||||
найти: F(x), M , |
D , P( 2 2); P( 1). |
|
|
|
||||||||||||
|
|
|
|
|||||||||||||
61
www.mitht.ru/e-library

Вероятность попадания с. в. ~ N(a; ) в заданный интервал b,c на основании (6.5) и (7.8) вычисляется по формуле:
c a |
b a |
|
|||||
P(b c) Ф |
|
Ф |
|
|
|
(7.9) |
|
|
|
|
|||||
|
|
|
|
|
|
||
Задачи для самостоятельного решения. |
|
||||||
Задача 7.1. |
|
M |
и D случайной вели- |
||||
Найти функцию распределения, |
|||||||
чины , распределенной равномерно на: а) отрезке |
1,3 ; б) |
||||||
отрезке 1,1 ; в) отрезке |
6,3 . Вычислить для |
каждого |
|||||
случая P( 4 0), P( 0,5), |
P( 2). |
|
|||||
Задача 7.2.
Случайная величина распределена по показательному за-
кону с параметром |
2. Найти |
f (x), F(x), M , |
D , |
P( 0,5), P( 1 |
1), P( 3), |
P( 2). |
|
Задача 7.3.
Случайная величина распределена по закону Коши, т.е. ее
плотность распределения |
имеет вид |
f (x) |
|
B |
, |
x R. |
|||
|
|
|
|
||||||
|
|
|
1 x2 |
|
|
||||
Найти B , F(x), M , |
D , |
P( 1 1), |
P( |
|
|
|
|
||
3). |
|
||||||||
Задача 7.4. |
|
|
|
|
|
|
|
|
|
2A
f (x) – плотность распределения случайной вели- ex e x
чины .
Найти A, F(x), P(0 2), P( 1).
Задача 7.5.
Найти среднюю скорость молекул газа и дисперсию скорости, подчиненной закону Максвелла:
60
P(A) 2 6 1
6 1 3; P(A C) 5
3; P(A C) 5 6; P(A C) 1
6; P(A C) 1 6; P(B C) 0.
6; P(B C) 0.
Пример 1.4.
Из четырех данных на карточках букв a,b,c,d наудачу выбирают две и составляют двухбуквенное слово.
1)найти пространство элементарных событий ;
2)определить N – число элементарных событий в ;
3)найти вероятность события B {слово начинается с буквы d }.
Решение.
1)В данной задаче состоит из следующих элементарных событий:
ab |
ba |
ca |
d a |
ac |
bc |
cb |
db |
ad |
bd |
cd |
dc |
2) При вычислении общего числа элементарных событий N заметим, что число столбцов элементарных событий равно числу букв, которые можно поставить на первое место в слове. Их четыре. При каждом конкретном выборе первой буквы число элементарных событий равно числу букв, которые можно поставить на второе место. Таких букв три. Поэтому общее число элементарных событий
N3 3 3 3 4 3 12.
3)Если слово начинается с буквы d , то это значит, что на первое место можно поставить букву одним способом, а на второе место – любую из оставшихся букв. Их три. Следовательно, число элементарных событий, составляющих B , рав-
но m 1 3 3. Согласно (1.1) P(B) m N 3
N 3 12 1
12 1 4. Часто в задачах число элементарных событий так вели-
4. Часто в задачах число элементарных событий так вели-
ко, что выписать их все не представляется возможным. Поэтому желательно даже в простых задачах рассматривать э- лементарные события в некотором порядке, указывающем алгоритм их образования.
9
www.mitht.ru/e-library

В общем случае можно пользоваться правилом умножения: если элемент z можно выбрать s способами, а элемент y можно выбрать k способами, то пару элементов zy можно выбрать s k способами.
Задачи для самостоятельного решения.
В следующих задачах найти пространство элементарных событий или указать алгоритм его получения. Считая элементарные события равновероятными, найти вероятность указанных событий.
Задача 1.1.
Какова вероятность того, что при бросании шестигранного кубика выпадет число очков, делящееся на 3?
Задача 1.2.
Из тщательно перемешанных костей домино наудачу берется одна. Какова вероятность того, что сумма очков на ней будет: а) равна четырём; б) равна шести; в) равна двенадцати; г) равна тринадцати; д) не менее девяти?
Задача 1.3.
Из пяти карточек с буквами А, Б, В, Г, Д наугад последовательно выбирают три и раскладываются в ряд. Какова вероятность того, что: а) получится слово «два»; б) трехбуквенное «слово» будет начинаться с буквы Б; в) «слово» будет содержать букву А, г) «слово» будет начинаться буквой Г и кончаться буквой Д; е) «слово» не будет содержать букву Б?
Задача 1.4.
Наудачу выбирают трёхзначное число. Какова вероятность того, что: а) оно не содержит нечётных цифр; б) сумма двух его последних цифр будет равна 17 ; в) сумма его цифр равна
4?
Задача 1.5.
Подсчитать вероятность того, что в наудачу выбранном пятизначном телефонном номере: а) все цифры окажутся раз-
10
2)Ф( x) Ф(x) (функция Лапласа нечетная);
3)Ф(x) монотонно возрастает на R ;
4)lim Ф(x) 0,5, lim Ф(x) 0,5;
x x
5) Разложение функции Лапласа в степенной ряд:
|
|
1 |
|
|
|
( 1) |
n |
x |
2n 1 |
|||||||
Ф(x) |
|
|
|
|
|
|
|
|
; |
|||||||
|
|
|
|
(2n 1) 2 |
n |
|
||||||||||
2 |
||||||||||||||||
|
|
|
n 0 |
|
n! |
|||||||||||
|
1 |
|
|
x2 |
|
|
|
|
|
|
|
|||||
|
2 |
|
|
|
|
|
|
|
||||||||
6) Ф (x) |
|
|
|
|
e |
. |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
2 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Таблица значений функции Лапласа приведена в Приложении I.
Таким образом, функция Лапласа Ф(x) должна занять место в ряду ходовых функций, используемых математиками, инженерами, технологами, экономистами и др., и в этом смысле формула y Ф(x) ничем не хуже и не лучше формул
y arctgx или y 5
 x3 .
x3 .
Функция распределения нормально распределенной с. в. с параметрами a и может быть выражена через функцию Лапласа:
1 |
x a |
|
|||
F(x) |
|
Ф |
|
|
(7.8) |
|
|
||||
2 |
|
|
|
||
Графики плотности распределения и функции распределения нормальной с. в. имеют следующий вид:
|
f (x) |
|
|
|
|
|
|
F(x) |
|
|
|
|||
|
|
|
|
|
|
|
|
|||||||
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
1 2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a a |
a |
x |
59 |
|
a |
x |
||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
www.mitht.ru/e-library
