
elteh_lections1-17
.pdfЛЕ К Ц И Я 1
1.Введение. Цели, задачи и структура курса.
2.Линейные цепи постоянного тока - основные понятия и определения.
3.Схемы электрических цепей и их элементы.
4.Законы Ома и Кирхгофа.
1.Введение
Электротехника - техническая дисциплина, которая занимается анализом и
практическим использованием для нужд промышленного производства и быта всех физических явлений, связанных с электрическими и магнитными полями.
Область практического применения электротехники имеет четыре связанные друг с другом направления :
1.Получение электрической энергии.
2.Передача энергии на расстояние.
3.Преобразование электромагнитной энергии.
4.Использование электроэнергии.
Научно-технический прогресс происходит при все более широком исполь- зовании электрической энергии во всех отраслях отечественной промышлен- ности. Поэтому электротехническая подготовка инженеров не электротехниче-
ских специальностей должна предусматривать достаточно подробное изучение вопросов теории и практики использования различных электроустановок. Ин- женер любой специальности должен знать устройство, принцип действия, характеристики и эксплуатационные возможности электрических цепей, элек- трических машин, различных аппаратов и другого электрооборудования, спо- собы регулирования и управления ими.
История развития электротехники как науки связана с важнейшими иссле- дованиями и открытиями. Это исследования атмосферного электричества, появление источников непрерывного электрического тока - гальванических элементов (1799 г.), открытие электрической дуги (1802 г.) и возможность ее использования для плавки металлов и освещения, открытие закона о направле- нии индуцированного тока (1832 г.) и принципа обратимости электрических машин, в 1834 г. впервые осуществлен электропривод судна, открытие закона теплового действия тока - закона Джоуля - Ленца (1844 г.), в 1876 г. положе- но начало практическому применению электрического освещения с изобрете- нием электрической свечи, в 1889-1891 гг. созданы трехфазный трансформа- тор и асинхронный двигатель.
Студенческий портал МИТХТ http://www.mitht.org
Внастоящее время отечественная электроэнергетика занимает передовые позиции в мире по созданию мощных ГЭС и каскадов электростанций, произ- водству мощных гидрогенераторов, высоким темпам теплофикации, строи-
тельству высоковольтных линий электропередач и мощных объединенных энергосистем, высокому техническому уровню электросетевого хозяйства.
Всовременных производственных машинах с помощью электротехнической
иэлектронной аппаратуры осуществляется управление ее механизмами, авто- матизация их работы, контроль за ведением производственного процесса, обеспечивается безопасность обслуживания и т.д. Все шире используется в технологических установках электрическая энергия, например, для нагрева из- делий, плавления металлов, сварки.
Основной задачей данного курса является получение основных сведений и формирование знаний, умений и навыков по электротехнике, электронным устройствам и электроприводу.
Всостав курса входят следующие разделы:
1.Электрические цепи постоянного тока.
2.Электрические цепи переменного тока.
3.Переходные процессы в электрических цепях.
4.Основы электроники.
5.Магнитные цепи и электромагнитные устройства.
6.Трансформаторы.
7.Электрические машины.
8.Основы электропривода.
2. Линейные цепи постоянного тока - основные понятия и определения.
Электрической цепью называется совокупность источников и потребителей электрической энергии, соединенных друг с другом с помощью проводников.
Электрический ток - направленное движение заряженных частиц (элек- тронов или ионов ).
Постоянный ток - ток, неизменный по величине и направлению.
Ветвью называется участок цепи между двумя соседними узлами, содержа- щий последовательное соединение элементов.
Точка, где соединяются три и более ветвей называется узлом.
Любой замкнутый путь, проходящий по ветвям данной цепи, называется контуром.
Основными параметрами, характеризующими электрические цепи постоян- ного тока, являются: I(А)- сила тока - количество электричества, проходяще- го через поперечное сечение проводника за единицу времени, U(В) - напря- жение на некотором участке электрической цепи, равное разности потенциалов на концах этого участка, R(Ом) - сопротивление, Р(Вт)- мощность. Все обо-
значения основных физических величин предусмотрены государственным стандартом. Единицы измерения диктуются международной системой единиц.
Студенческий портал МИТХТ http://www.mitht.org
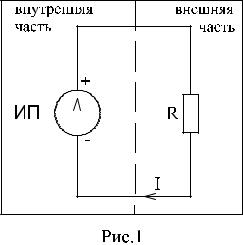
3. Схемы электрических цепей и их элементы.
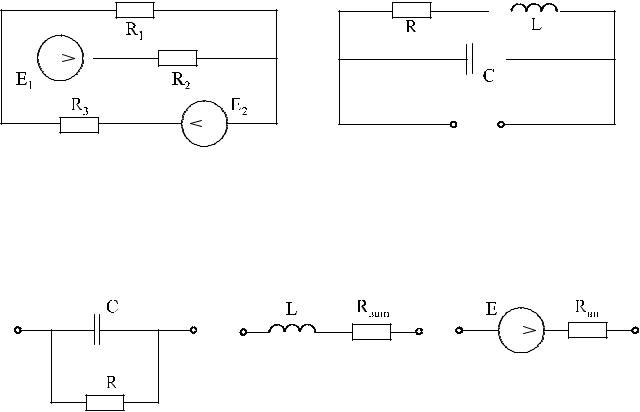
Графическое изображение электрической цепи и ее элементов называется электрической схемой (рис. 1)
На любую машину, в состав которой входят электрические устройства, кроме конструкторских чертежей имеется элек- тродокументация, состоящая из различных
электрических схем. Электрические функ-
циональные схемы раскрывают принцип действия устройства. Существуют элек- тромонтажные схемы, в которых раскры- вается монтаж (соединение) электриче-
ских элементов цепи.
Электрические принципиальные схемы раскрывают электрические связи всех от-
дельных элементов электрической цепи между собой.
Все схемы вычерчиваются по определенным стандартам- ГОСТам. ГОСТы являются основой технического языка, применяемого в масштабе всей стра- ны.
Кроме основных электрических схем существуют схемы замещения, по ко- торым наиболее удобно составлять математические уравнения, описания элек- трических и энергетических процессов. Такие схемы являются эквивалентными моделями электрической цепи. Схемы максимально упрощены и по ним удоб- нее провести анализ отображаемых ими сложных электрических цепей.
Все элементы электрических цепей можно разделить на три группы: ис- точники (активные элементы), потребители и элементы для передачи элек- троэнергии от источников к потребителю (пассивные элементы).
Источником электрической энергии (генератором) называют устройство, преобразующее в электроэнергию какой-либо другой вид энергии (электро- машинный генератор - механическую, гальванический элемент или аккумуля- тор - химическую, фотоэлектрическая батарея - лучистую и т.п.).Источники делятся на источники напряжения (Е,U=соnst, при изменении и I) и источники тока (I=соnst, при изменении U). Все источники имеют внутреннее сопротив- ление Rвн, значение которого невелико по сравнению с сопротивлением других элементов электрической цепи .
Приемником электрической энергии (потребителем) называют устройство, преобразующее электроэнергию в какой-либо другой вид энергии (электро- двигатель - в механическую, электронагреватель - в тепловую, источник света - в световую (лучистую) и т.п.).
Студенческий портал МИТХТ http://www.mitht.org
Элементами передачи электроэнергии от источника питания к приемнику служат провода, устройства, обеспечивающие уровень и качество напряжения и др.
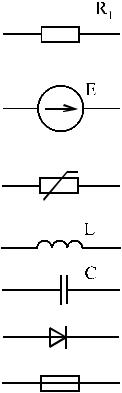
Условные обозначения элементов электрической цепи на схеме стандарти- зованы. Примеры:
- резистивный элемент (линейный),
- идеальный источник ЭДС, условно положи- тельное направление ЭДС принято от отрица- тельного полюса к положительному (и совпа- дает с положительным направлением тока)
- нелинейный элемент,
- индуктивный элемент, - емкостной элемент,
- полупроводниковый диод, - плавкий предохранитель
4. Законы Ома и Кирхгофа
Закон Ома в простейшем случае связывает величину тока через сопротив- ление с величиной этого сопротивления и приложенного к нему напряжения:
I = U / R; |
U = IR. |
Сила тока на некотором участке электрической цепи прямо пропорциональ-
на напряжению на этом участке и обратно пропорциональна сопротивлению этого участка.
Закон Ома справедлив для любой ветви (или части ветви) электрической цепи, в таких случаях его называют обобщенным законом Ома. Для ветви, не содержащей ЭДС, закон Ома запишется:
I = |
ϕa −ϕb |
= |
Uab |
. |
|
|
|||
|
n |
n |
||
|
åRi |
åRi |
||
|
1 |
|
1 |
|
Здесь ϕа ,ϕb - потенциалы крайних точек ветви, их разность можно заменить напряжением Uab.
Студенческий портал МИТХТ http://www.mitht.org
Обобщенный закон Ома для ветви, содержащей ЭДС (т.е. для активной вет- ви):
|
k |
|
|
k |
|
I = |
ϕa −ϕb + åEj |
= |
Uab + åEj |
||
1 |
1 |
||||
|
|
||||
|
n |
|
|
n |
|
|
åRi |
|
|
åRi |
|
|
1 |
|
1 |
||
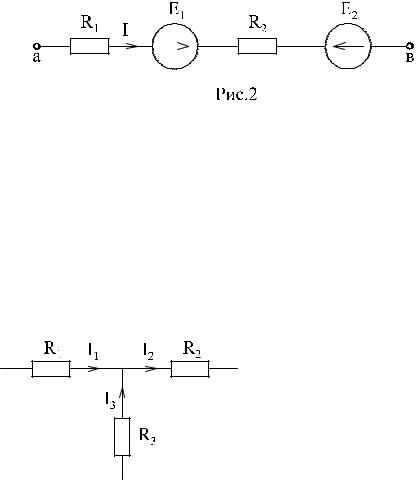
Пример: Записать закон Ома для активной цепи на рис. 2.
I = ϕa −ϕb + E1 − E2
R1 − R2
Первый закон Кирхгофа
Алгебраическая сумма токов, сходящихся в любом узле электрической цепи равна нулю. При этом токи, текущие к узлу считаются положительными, а от узла - отрицательными. Другая формулировка: сумма токов, подходящих к уз- лу, равна сумме токов, отходящих от узла.
n |
|
|
åIk = 0 |
||
k =1 |
+ I3 = 0 или |
|
I1 |
− I2 |
|
I1 |
+ I3 |
= I2 |
Первый закон Кирхгофа по сути является законом баланса токов в узлах цепи.
Студенческий портал МИТХТ http://www.mitht.org
Второй закон Кирхгофа
В любом замкнутом контуре электрической цепи алгебраическая сумма па- дений напряжений на элементах, входящих в контур, равна алгебраической сумме ЭДС.
m |
n |
åRk Ik = åE j |
|
k =1 |
j=1 |
Второй закон Кирхгофа по сути является законом баланса напряжений в контурах электрических цепей.
Для составления уравнения по 2-му закону Кирхгофа выбирается произ- вольное направление обхода контура. Тогда, если направление тока в цепи совпадает с направлением обхода, то соответствующее слагаемое берется со знаком "+", а если не совпадает, то со знаком "-". Аналогичное правило рас- становки знаков справедливо и для ЭДС.
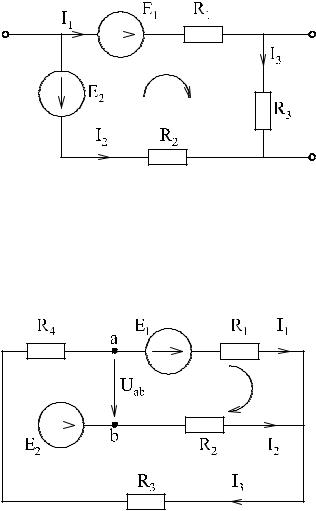
Пример:
R1I1 + R3I3 − R2 I2 = E1 − E2
Уравнение по 2-му закону Кирхгофа может быть записано и для контура, имеющего разрыв цепи, однако при этом необходимо в уравнении учитывать напряжение между точками разрыва.
Пример:
R1I1 − R2 I2 −Uab = E1
Студенческий портал МИТХТ http://www.mitht.org
ЛЕ К Ц И Я 2
1.Схемы замещения электрических цепей.
2.Эквивалентные преобразования пассивных электрических цепей.
3.Расчет цепей посредством двух законов Кирхгофа.
4.Мощность в цепях постоянного тока.
5.Баланс мощностей.
1.Схемы замещения электрических цепей.
Схемой электрической цепи называется ее графическое изображение с ис- пользованием обозначений идеальных элементов. Например:
Если учесть сопротивление утечки реального конденсатора, сопротивление
витков реальной индуктивной катушки и внутреннее сопротивление реального источника ЭДС, то можно составить соответствующие схемы замещения этих элементов:
Отсюда следует, что все схемы по сути дела являются лишь более или ме- нее точными схемами замещения реальных электрических цепей.
Представленный на рис.2 контур содержит три участка: участок с посто- янным напряжением U = Е, не зависящим от тока источника, и участки с на- пряжениями RвхI и U на нагрузке Rн.
Направление ЭДС выбрано совпадающим с направлением тока, но оно противоположно напряжению на этом элементе.
Для определения параметров схемы замещения источника электрической энергии с линейной внешней характеристикой нужно провести два опыта - холостого хода (I=0; U=Uх=Е) и короткого замыкания (I=Iк; U=Е-RвнI).
Студенческий портал МИТХТ http://www.mitht.org
2. Эквивалентные преобразования пассивных электрических цепей.
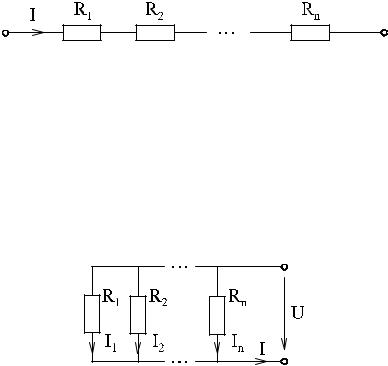
Для упрощения анализа сложных электрических цепей отдельные их уча- стки, не содержащие ЭДС, или пассивные цепи целиком можно заменить од- ним эквивалентным сопротивлением. Под эквивалентным понимают такое сопротивление, которое, будучи включенным в цепь вместо заменяемой группы сопротивлений, не изменяет распределение токов и напряжений в ос- тальной части цепи.
При последовательном соединении сопротивлений по каждому из них
протекает один тот же ток, следовательно, падение напряжения на эквива- лентном сопротивлении должно быть равно сумме падений напряжений на ис- ходных сопротивлениях:
IRэкв = IR1 + IR2 +...+ IRn
отсюда получаем:
n
Rэкв = R1 + R2 +...+ Rn = åRi
1
Если группа заменяемых сопротивлений соединена параллельно, то
напряжения на каждом из них и на эквивалентном сопротивлении одинаковы. Условия эквивалентности будут выполнены, если ток через искомое сопро- тивление будет равен сумме токов через отдельные параллельные сопротив- ления:
I = I1 + I2 +...+ In
Используя закон Ома для отдельного сопротивления, можем записать:
|
|
|
U |
|
= |
U |
|
+ |
U |
+...+ |
U |
|
|
|||||
|
|
|
R |
|
R |
R |
R |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Окончательно получаем: |
|
экв |
|
|
1 |
|
|
|
2 |
|
|
|
n |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
|
1 |
|
|
1 |
|
|
|
|
1 |
|
n |
1 |
||||
|
|
|
= |
|
+ |
|
|
+...+ |
|
= å |
|
|||||||
|
R |
|
R |
R |
|
R |
R |
|||||||||||
|
экв |
|
|
1 |
|
|
2 |
|
|
|
n |
|
1 |
i |
||||
Поскольку величина, обратная сопротивлению, есть проводимость, то, вводя обозначения для проводимости Gi =1/ Ri , получим:
Студенческий портал МИТХТ http://www.mitht.org
n
Gэкв = åGi
1
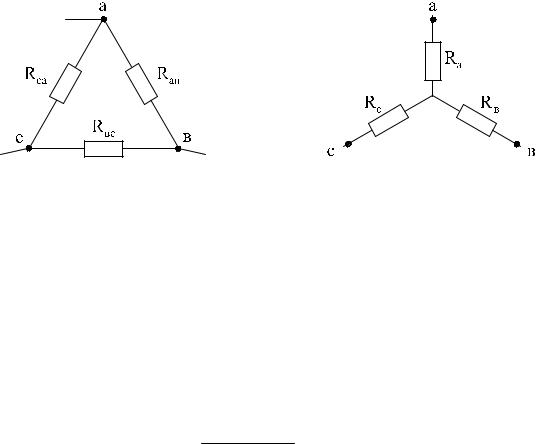
При анализе сложных схем встречаются случаи, когда часть схемы образу- ет так называемый треугольник сопротивлений:
Схема упрощается, если треугольник с сопротивлениями Rав, Rвс, Rса за- менить эквивалентной звездой с сопротивлениями Rа, Rв, Rс. Иногда, наобо- рот, необходимо обратное преобразование звезды в треугольник. Схемы тре- угольника и звезды считаются эквивалентными, если после преобразования все токи и напряжения в остальных частях схемы (не затронутых преобразова- ниями) остаются неизменными.
Очевидно, условия эквивалентности должны выполняться и при обрыве проводов, подходящих к узлам "а", "в", "с". Например, при обрыве провода, подходящего к узлу "а", сопротивления между точками "в" и "с" в треуголь- нике и звезде должны быть одинаковы, т.е.:
Rbc (+Rac ++Rab ) = Rb + Rc ;
Rbc Rca Rab
Рассуждая аналогичным образом, можно записать:
Rca (Rab + Rbc ) |
= R + R ; |
|
|
||
|
c |
a |
Rca + Rab + Rbc |
|
|
Rab (Rbc + Rca ) |
= R + R ; |
|
|
||
|
a |
b |
Rab + Rbc + Rca |
|
|
Решая полученную систему уравнений относительно Rа, Rв и Rс, получим формулы эквивалентного преобразования треугольника в звезду:
Ra = |
Rab Rca |
; |
|
Rab + Rbc + Rca |
|||
|
|
Студенческий портал МИТХТ http://www.mitht.org

Rb = |
Rbc Rab |
; |
||
Rab + Rbc + Rca |
||||
|
|
|
||
Rc = |
|
Rca Rbc |
; |
|
|
Rab + Rbc + Rca |
|||
|
|
|
||
Решая систему относительно Rab , Rbc и Rca получим формулы преобразова- ния звезды в треугольник:
Rab = Ra + Rb + Ra Rb ;
Rc
Rbc = Rb + Rc + Rb Rc ;
Ra
Rca = Rc + Ra + RRc Ra ;
b
В частном случае, когда сопротивления звезды или треугольника одина- ковы, эти формулы упрощаются:
RY = 13 R
R= 3RY
3.Расчет цепей посредством двух законов Кирхгофа.
Порядок расчета:
а) произвольно задаются положительными направлениями токов во всех ветвях схемы,
б) для всех узлов схемы кроме одного составляются уравнения по 1-му за- кону Кирхгофа,
в) для всех независимых контуров составляются уравнения по 2-му закону Кирхгофа (контур будет считаться независимым от остальных, если в него вхо- дит хотя бы одна новая ветвь, т.е. не вошедшая в состав других контуров).
Общее число уравнений, составленных по 1 и 2-му законам Кирхгофа должно быть равно числу неизвестных токов. Полученная система линейных уравнений разрешается относительно токов с использованием известных ме- тодов решения систем уравнений (например, с помощью определителей)
Студенческий портал МИТХТ http://www.mitht.org
