therm_lections1-9

Из последнего уравнения получаем зависимость удельной производительности установки по жидкой фазе:

1 – x = (h2 – h1) / (h0 – h1) или 1 – х = (h1 – h2) / (h1 – h0) кг жидк. фазы/кг исходного газа. (8.1)

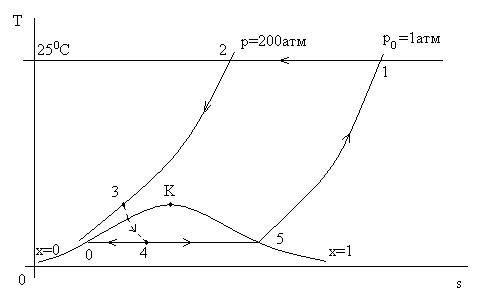
В числителе дроби в этой формуле стоит величина теплоты, взятая от газа в процессе изотермической компрессии в процессе 1 – 2 (см. рис. 8.4). В знаменателе – общее количество теплоты, которое необходимо отнять от газа, начиная с исходного состояния (точка 1) и кончая жидкой фазой (точка О).

Впрочем, степень сухости х = х3 легко определить по фазовой диаграмме или по соответствующим таблицам. Для этого достаточно знать давление после компрессора и положение точки 24 (см. рис. 8.4). Отсюда легко определяется степень влажности влажного пара 1 – х = 1 – х3 в точке 3.

Удельная работа сжатия воздуха в компрессоре рассчитывается стандартно (см. лекцию 2) как работа при изотермическом процессе:

wK = R0/M T1ln p/p0, Дж/кг исходного газа, (8.2)

где R0 = 8314 Дж/кмоль К – универсальная газовая постоянная, М - кг вещества/кмоль молекулярный вес вещества, р0 и р – атмосферное давление и давление после компрессии соответственно. В формуле (8.2) не учитывается изотермический и механический КПД компрессора. Впрочем, учесть их не составляет труда. На рис. 8.4 wK соответствует площади внутри цикла 1 – 2 – 24 – 3 – 5 – 1, а сама площадь зрительно напоминает парус.

Мощность на валу компрессора определяется как:

где G – массовая производительность по исходному воздуху, кг. исходного воздуха/с. Основная экономическая характеристика цикла – удельная работа на 1 кг. жидкой

фазы:

wЖ = wK/(1 – x), Дж/кг. жидкой фазы. (8.4)

Именно по этому показателю цикл Гампсона не находит промышленного применения. Эта установка хороша в научных лабораториях по своей надежности и простоте запуска, но получаемая жидкая фаза дороговата.

Физической и термодинамической основой уменьшения величины wЖ являются следующие простые соображения. Прежде всего, следует уменьшать площадь «паруса» (см. рис. 8.4). А этого можно достигнуть только уменьшением давления сжатия. Такие установки глубокого холода и среднего давления существуют в промышленной практике. Кроме того, необходимо уменьшать степень сухости влажного пара в точке 3. Этого можно достигнуть, если опустить точку 24 по изобаре р = const вниз (см. рис. 8.4). Но опустить эту точку вниз, по существу означает еще больше отвести теплоты от сжатого газа.

Последнюю рекомендацию реализовал проф. Линде: теплообменник Сименса он разделил на две части, а в промежутке поставил теплообменник от установки умеренного холода. Общие затраты работы на ожижение увеличиваются, но увеличение количества жидкой фазы в целом уменьшает величину wЖ.

Пример. Определить количество получаемого в 1 час жидкого воздуха и необходимую для этого мощность компрессора при переработке 200 кг исх. возд / час, сжатого до давления р = 200 атм. Установка работает по схеме Линде. Температура до и после компрессии 250С.

Воздух дросселируется до давления р0 = 1 атм. Потери «холода» в окружающую среду принять равными 4,19 кДж/нм3. Недорекуперация составляет 50С. Эффективный коэффициент полезного действия (КПД) компрессора – ηэфф = 0,62.

Решение. Глядя на формулу (8.1), необходимо найти величины энтальпии воздуха в характерных точках цикла (см. рис. 8.6).

Рис. 8.6. Иллюстрация к решению задачи примера. Сравните с рис. 8.4.

По таблицам или по фазовой диаграмме для воздуха находим:

h0 = 92,1 кДж / кг. исх. возд., h1 = 510 кДж / кг исх. возд., h2 = 474 кДж / кг исх. возд.

Потери теплоты на недорекуперацию (не доохлаждение) рсчитываются (см. лекцию 2)

qp = cpm|0T t = 1,01*5 = 5,05 кДж / кг исх. возд.

Здесь среднюю массовую изобарную теплоемкость срm|0Т нашли по таблицам теплоемкости для воздуха, приняв Т = 250С.

Потери «холода», т.е. приток теплоты из окружающей среды в холодильную систему,

равен:

q0 = 4,19 / ρн ,

где ρн – плотность воздуха при нормальных условиях. Здесь можно воспользоваться справочником, а если его нет под рукой, то просто рассчитать:

pv = RT → ρн = p0 /RT0 = 105 * 29 / (8314*273) = 1.29 кг возд. / нм3.

Отсюда потери «холода» равны q0 = 4,19 / 1,29 = 3,25 кДж / кг исх. возд

.

Степень ожижения рассчитываем по формуле (8.1), но с учетом потерь:

1 – x = (h1 – h2 – q0 – qp) / (h1 – h0) =

= (510 – 474 – 3,25 – 5,05) / (510 – 92,1) = 0,063 кг жидк. возд./ кг исх. возд.

Удельная работа компрессора (см. (8.3)), но с учетом КПД, равна:

wк = R0/Mηэфф Т1ln p/p0 = 8,314*298*ln(200/1) /(29*0,62) =730 кДж / кг исх. возд.

Удельная работа, отнесенная к 1 кг. жидкого воздуха, равна:

wж = wк / (1 – х) = 730 / 0,063 = 11,6*103 кДж / кг жидк. возд.

Теперь все готово для ответов задачи. Количество получаемого жидкого воздуха равно:

g = G*(1 – x) = 200*0,063 = 12,6 кг жидк. возд./час.

Затрачиваемая мощность для переработки воздуха равна:

Nк = G*wк = 200*730 / 3,6*103 = 40,5 кВт.

Ответ: расход жидкого воздуха из установки 12,6 кг жидк. возд. / час, мощность компрессора на ожижение 40,5 кВт.

Комментарий к задаче и ее ответам. Сколько стоит 1 кг жидкого воздуха? Сегодня за электроэнергию платят в промышленности примерно 5 рублей за 1 кВт-час.

1 кВт-час = 1кДж/с * 3600 с, или 1 кДж = 1/3600 кВт-час.

Тогда стоимость 1 кг жидкого воздуха равна:

11,6*103*5 / 3600 = 16,1 рубля / кг жидк. возд.

Каждый час придется платить за электроэнергию сумму

16,1 * 12,6 = 203 рубля / час.

В целом сжатый воздух получился дороговатым. Основная причина в том, что давление сжатия велико (р = 200 атм), и потому площадь «паруса» (см. рис. 8.6) тоже велика. Кроме того, точка 3 на рис. 8.6 находится на изобаре р = 200 атм так высоко, что после дросселирования точка 4 близка к точке 5. Иными словами, во влажном паре воздуха мало жидкой фазы. В целом малая эффективность обусловлена тем, что западные ученые – термодинамики стремились попасть в двухфазную область слева, делая давление сжатия выше критического. А почему бы не справа?

Несколько слов о холодильном цикле нашего соотечественника Петра Леонидовича Капицы. Находясь в научной командировке в Англии в одной из лабораторий Кембриджа, ему удалось создать уникальную газовую турбину (адиабатный расширитель сжатого газа) с огромным для того довоенного времени КПД около 80%. Это сразу позволило отказаться от дросселирования и использовать адиабатное расширение газов для получения низких температур. В терминах этой лекции, это позволило сместить точку 3 (см. рис. 8.4) влево по изобаре р0 = const (она же изотерма Т = const) в область малых степеней сухости. Следовательно, производительность установки по жидкому воздуху резко возросла.

Кроме того, П. Л. Капица решил уменьшить давление сжатия ниже критического и это позволило использовать турбокомпрессор для сжатия газа, производительность которого много больше поршневого. Иными словами, площадь «паруса» на рис. 8.4 резко уменьшилась

(теперь процесс «входит» в двухфазную область справа от фазовой кривой х = 1). Здесь удалось и уменьшить числитель в (8.4), и увеличить знаменатель там же. Все это резко удешевило производство жидких газов и сделало его привлекательным для промышленности.

В довоенные годы в СССР стали срочно создавать установки ожижения и разделения воздуха, используя цикл П.Л. Капицы. Промышленное производство технического кислорода в довоенные и военные годы в СССР позволило использовать его прежде всего в металлургии. В доменных печах при производстве чугуна, в мартеновских и бессемеровских печах при производстве сталей полученный кислород применялся в качестве дутья. Это позволило избавиться от вредных для прочности примесей серы, мышьяка, фосфора и азота. После легирования таких сталей они приобретали очень большую прочность.

Это позволило делать танки Т – 34 с прочной и легкой броней, не поддающейся немецкой артиллерии. Уменьшение веса брони сделало этот танк более маневренным, увеличило его скорость, проходимость (даже по минским болотам), позволило увеличить величину боезапаса и запаса топлива.

А если еще вспомнить, что на танках Т – 34 стояли дизельные двигатели (их КПД много больше бензиновых, которые были у немецких танков), то становится понятным, что танк Т – 34 недаром признан лучшим танком второй мировой войны. Так термодинамика воевала с фашистскими захватчиками, которые позволили себе пренебречь вторым законом термодинамики: только большие затраты всех ресурсов позволяют достичь самых скромных успехов.

Лекция 9.

Н.Н. Прохоренко.

Беден не тот, у кого мало вещей, а тот, кому мало.

Богатый всегда беден.

Термодинамика коммерческого банка.

Всвоей полушутливой классификации наук Л. Ландау назвал естественные науки - естественными, гуманитарные - неестественными, а математические - сверхъестественными. Кажется, центр тяжести в банковском деле находится в неестественных науках. Отечественная литература по банковскому делу, изданная до 1995 года, отличается невразумительностью и эклектичностью. Необходимо серьезное проявление воли и упорства, чтобы дочитать эти монографии до конца в надежде выяснить что-то содержательное. Надежды были тщетны, и причина этого в одном: история банковского дела в России насчитывает всего-то несколько лет, а в Западной Европе - 500 лет, в США - чуть больше 200 лет. Поэтому отечественное банковское дело находится совершенно в эмбриональном состоянии, основные физические явления, закономерности просто еще не успели себя проявить, влияние патологических начальных условий доминирует во всем.

Воснову дальнейшего рассмотрения в этой главе положена замечательная книга, конечно же, иностранного автора и, конечно же, о банковском деле развитых капиталистических стран. Следовательно, содержательная часть этой лекции имеет малое отношение к современным банковским деятелям России. Может быть, дети или внуки сегодняшних банкиров заинтересуются термодинамикой своей фирмы.

Физико-содержательной основой классической термодинамики является закон сохранения энергии, который в сочетании с уравнениями состояния рабочего тела делает термодинамику и инструментом познания и расчетно математическим аппаратом.

История развития термодинамики показывает, что она в своих истоках носит черты феноменологичности, да и сама форма выражения закона сохранения энергии претерпевала существенные изменения. Эти два обстоятельства и вдохновили автора на применение термодинамического анализа к такому изысканному для пост советского времени фрукту, каким является коммерческий банк.

Главным «know how» дальнейшего рассмотрения является очень простая идея: положить в основу термодинамического анализа любой другой закон сохранения, а не только закон сохранения энергии, используя методологию и инструментарий классической термодинамики, имидж и авторитет которой у физиков и представителей точных наук (но не банкиров) недосягаемо высокий. Реализация этой идеи позволяет рассмотреть не только коммерческий банк, но и оптовую торговую фирму, финансово-промышленный концерн, бандитское формирование и т.п. организацию, занимающуюся добычей прибыли из внешнего мира.

1. Физические представления и гипотезы, формализация закона сохранения

Принципиальным отличием естественных наук от «не естественных» является отсутствие у последних переменных, в которых необходимо думать. Поэтому приведем несколько определений понятий, позволяющих в дальнейшем банковскому работнику понять физика.

1.Параметром состояния системы называется физическая величина, которая по мнению исследователя существенно определяет поведение системы. Заметим, что ключевыми словами здесь являются «физическая величина». Она характеризуется двумя составляющими: физическая величина это отвлеченное число + наименование, название ее. Например, длина ресниц секретарши президента банка может быть параметром состояния коммерческого банка: это действительно физическая величина и ее несложно измерить. Предостережем не физиков, что математические операции над отвлеченными числами не всегда можно проводить над физическими величинами. Например, операция алгебраического сложения имеет смысл над физическими величинами только одинаковой размерности. Складывать танки и ромашки нехорошо.

2.Потенциалом некоторого взаимодействия системы с внешней средой называется такой параметр состояния, разность значений которого в системе и во внешнем мире является необходимым условием обмена (энергией, массой, количеством движения, информацией и ....

деньгами) системы с внешней средой.

3.Координатой состояния этого рода взаимодействия называется такой параметр состояния, изменение которого в системе (и, конечно, во внешнем мире) является достаточным условием обмена.

4.Уравнением состояния системы называется зависимость потенциала от всех координат.

5.Элементарным количеством воздействия внешнего мира данного рода на рассматриваемый объект называется произведение потенциала на приращение (дифференциал) координаты того же рода взаимодействия.

6.Первый закон термодинамики это запись закона сохранения некоторой субстанции: дифференциал ее равен сумме элементарных количеств воздействия всех родов внешней среды на рассматриваемую систему.

Итак, каждый род взаимодействия характеризуется своим потенциалом и координатой, а если последняя меняется, то и количеством взаимодействия. Далее, из этих определений понятий следует: сколько родов взаимодействия, столько потенциалов и столько уравнений состояния, столько слагаемых в первом законе термодинамики.

Чтобы понять, чем занимается коммерческий банк, каковы взаимодействия его с внешней средой, рассмотрим технологическую схему типичного коммерческого банка на рис. 9.1.

Банк территориально расположен в некотором регионе, население которого получает доходы от своей деятельности. Часть доходов уходит на потребление (ради этого и осуществляется эта деятельность), остаток образует накопление. Физические лица делают накопления для приобретения дорогостоящих товаров, предметов потребления и услуг. Юридические лица (корпоративные вкладчики), открыв свой счет в банке, делают накопления для обновления производства, приобретения нового оборудования, для расширения производства.

Эти накопления вкладчики приносят в банк, и их деньги являются сырьем для банка, для совершения некоторых переделов над этим сырьем. Все вклады собираются в емкость под названием «актив». Каждый вклад и все разнообразие вкладов характеризуется суммой вклада, сроком возврата и банковским % по вкладу.

где %БАНКА( ) - банковский процент по вкладу, выраженный не в %, а в долях. Размерность его (день)-1. %ИНФ( ) - процент инфляции, (день)-1. Заметим, что невежественный вкладчик не подозревает об инфляции, т.е. уменьшения меновой стоимости его денег за время

вклада. К моменту времени + , где - срок депозита

Заметим, что %БАНКА( ) здесь записан функцией от времени. Наш дорогой сбербанк позволяет себе без согласия и уведомления вкладчиков менять %БАНКА , как в любой

бандитской стране. То обстоятельство, что %ИНФ( ) является функцией от времени чувствует, хотя и не понимает, любая старушка в магазине: «Опять цены выросли!»

Величина прибыли вкладчика в меновой стоимости равна:

Чтобы отразить стремление биологического вида homo sapience не просто к «халяве», а к

быстрой «халяве», разделим норму прибыли на время депозита . Тогда потенциалом PN воздействия вкладчиков на банк (или банка на вкладчиков) назовем именно эту скорость нормы прибыли:

рублей прибыли / рубль затрат* день.

Обращаем внимание читателя с гуманитарным образованием, что 1 рубль в кармане покупателя 1 рублю в банке, 1 рублю налога, 1 рублю прибыли; что 1% налога 1%

инфляции 1 % банка 1% кредита и т.д. Вроде бы, там рубли, там %-ты, но это разные рубли и %-ты, т.е. разные физические величины, так как они имеют разное наименование.

Всякий банк имеет собственный капитал, который он пускает по внутреннему контуру (см. рис. 9.1), чтобы получить доход от кредитных операций. А так как банковские владельцы капитала принадлежат к тому же биологическому типу, что и вкладчики, то выражение PN

будет тем же, только их %БАНКА( ) 0, но для нашей модели это не существенно.

В качестве координаты состояния, обусловленного этим видом воздействия, примем одномоментное количество накоплений N, находящихся в распоряжении банка. В величине N находятся средства частных и юридических лиц, кредит от «дружественных» банков и собственные высоко ликвидные средства. Размерность N - рубли.

2. Воздействие заемщиков капитала. Повторимся, что при всем разнообразии операций, процедур и услуг заемщикам капитала все они носят кредитный характер. Разобьем всю сумму активов банка на две части:

D D 1 D, 0 1

где - доля активов, направленных на операции с ценными бумагами, и 1 - - доля,

направленная на кредитование промышленности, торговли и производства услуг. Величину определяет руководство коммерческим банком или акционерное собрание.

Рассмотрим операции с ценными бумагами (векселями, валютой, государственными казначейскими облигациями, акциями каких-то фирм и т. д.). Пусть X0 - стоимость ценной

бумаги у эмитента (продавца), который гарантирует некоторый доход в виде % от X0 через

какой-то промежуток времени дней. Пусть X - рыночная стоимость этой ценной бумаги на рынке. Биржевой курс ценной бумаги, выраженный не в %, а в долях от 1, представляется в виде:

X X0 X0

Если > 0, да еще и увеличивается от торга к торгу, то предприятие - эмитент неплохо

работает, если уменьшается и становится отрицательным, то такое предприятие явно разоряется.

Если банк покупает ценные бумаги с общей стоимостью X0 эмитента, то на рынке он затратит

D X0 1 , рублей.

После реализации ценных бумаг, после их погашения эмитент обязан выдать владельцу сумму X0 плюс доход %*X0 рублей. Следовательно, доход банка от операции с ценными бумагами составит величину:

X0 1 % D D 1 % D 1

Из этого выражения следует, что не отрицательность дохода будет при % , т.е. биржевой курс ценной бумаги должен не превосходить доходности ее, иначе банк потерпит убыток.

Прибыль получается после уплаты налогов государству, т.е.

Скорость нормы прибыли получим делением нормы прибыли на время операции с ценными бумагами :

1 %налога 1 % 11 рублей прибыли / рубль затрат в день.

Рассмотрим процесс кредитования банком промышленности, торговли и производства услуг. Если банк дает кредит в размере (1 - )D рублей, то хочет получить через КРЕДИТ дней

Координатой состояния второго рода взаимодействия банка с внешним миром принимаем всю сумму кредитов D, одномоментно находящихся на руках заемщиков капитала. Говоря «банковским» языком, D представляет собой работающие (рисковые) активы.

3. Третий род взаимодействия. Само существование банковского механизма в некоторой среде невозможно без затрат на свое бытие. Банк должен платить за аренду помещения или земли, платить городу за коммунальные услуги, за все виды связи и энергию, за банковское оборудование и его обслуживание, приходится платить за охрану и заработную

плату банковским наемным служащим и т.д. и т.п. Все эти затраты Z( ) по существу определяют себестоимость 1 рубля прибыли, ради которой и организован сам банк.

Часть этих затрат банку удается взвалить на плечи своих клиентов: банк требует оплаты за процедуру любого движения денег вкладчиков, владельцев счетов и заемщиков капитала,

Обозначим этот новый груз на клиентов как ZZ( ) рублей поборов / год.

Потенциалом третьего рода взаимодействия внешней среды с банком назовем величину:

операций, процедур и услуг может производить банк, тем, вообще-то, он больше привлекает к себе клиентов, но, одновременно, и больше поле проявления хаоса, беспорядка, ошибок персонала, сбоев и отказов банковского механизма. Если банк делает i = 1,2,3,...i0 операций, процедур и услуг, и если каждая из них востребована mi раз в год, а общее их число M, то mi /

M Pi есть частота свершения i-ой операции. Вводим меру разнообразия операций в банке по Шеннону:

и отказов банковского механизма, безграмотные решения руководства, администраторов всех рангов разобьем на отдельные, узкие, специфичные группы. Пронумеруем эти группы j = 1,2,3,...j0 . Из статистического анализа состояния банка за какой-то период времени можно получить вероятность отказов по каждой группе P1,P2,P3,....Pj0 . Вводим меру хаоса и беспорядка в банке тоже в манере Шеннона

Может быть, банковским деятелям будет интересно узнать, что максимум S1 и S2 наступает при P1 = P2 = P3 =.... и эти максимумы равны max S1 = ln i0 и max S2 = ln j0 .

Третьей координатой состояния примем величину S = S1 + S2 .

Приведем уравнения состояния (9.1 – 9.3) PN , PD , PS = f(N, D, S) от общего вида к наивозможно явной связи с операционными банковскими характеристиками, т.е. аргументами задачи N, D, S.

Сразу отметим экспериментальный факт в деятельности банков: время кредитных

операций КРЕДИТ, как правило, меньше времени депозита , времени вклада денег населением в банк. Последний старается много раз пропустить эти деньги по внутреннему

технологическому контуру, получая доход при каждом таком обороте. Обозначим буквой число таких оборотов. Тогда

кредита, 1