Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный университет тонких химических технологий им. М.В. Ломоносова

Предмет:

Коллоидная химия

Файл:

kolda

.pdf

Скачиваний:

101

Добавлен:

24.03.2015

Размер:

1.41 Mб

Скачать

☆

1 / 21 2 > Следующая >>>

. Предметколлоиднойхимии.Почемуповерхностныеявленияидисперсныесистемыизучаютсяврамкаходной

Система

а, м

дисциплины-коллоиднойхимии?Значениеколлоиднойхимиидлятехнологии.

1 Область истинных растворов молек степени

<10

Коллоидная химия - это наука о поверхностных явлениях и гетерогенных дисперсных системах. Эти сист.

дисперс-ти

занимают промеж положение между истин растворами и грубыми дисперсиями и по меньшей мере двух

2 Коллоидная (ультрамикрогетерогенная), частицы

фазные. Размер частицы 10^-7 до 10^-9 (м) представляют собой агрегаты молекул. С увеличением степ.

- 10

Раздробленности доля молекул на пов-ти возрастает. Для ч-цы кубической формы эта завис-ть проходит

видимы в электронный микроскоп

через мах в соответствии длине ребра куба. В этом случае пов-ть количественно станов партнером объемной

10 7

фазы и как следствие роль пов-ных явлений для таких сист-м значительно возрастает, поэтому пов-ные явл-ия

3 Микрогетерогенная, частицы видны в обычный

и диспер-ые системы изуч. В рамках 1 дисциплины.

микроскоп

Коллоидная химия служит обоснованием многих технологических процессов, таких как дробление,

смешение, переработка полимеров. Геология также тесно связана с коллоидной химией.

Грубодисперсная,

частицы

видны

2. Признакиобъектовколлоиднойхимии:гетерогенностьидисперсность.

невооруженным глазом

Признаки является необходимым, но недостаточным для отнесения

системы к коллоидной. Гетер-ть качественный признак объектов

коллоидной химии, он указывает на наличие межфазной поверхности.

4 Классификациядисперсныхсистемпоагрегатномусостояниюдисперснойфазыидисперсионнойсреды.

Существование межфазной пов-ти предполагает межфазного натяжения.

Дисперсионная среда

Дисп. фаза

Условное обозначение

пример

Величина пов-ного натяжения (ПН) опред-т степень различия между

Твердая

Тв.

Т/Т

Сплав

контактними фазами. Чем выше гетерогенность, тем выше ПН. Молек на

Жидкая

Ж/Т

Пористые сист.

пов-ти принадлежат обеим фазам поэтому их состояние отлич от

Газообр

Г/Ж

Почвы, Пенза

состояния молекул в объеме. Молекулы в этом слое находятся в несимметричном силовом поле.

Жидкая

Тв.

Т/Ж

Суспензии, зол

Молекулярные силы в поверхностном слое некомпенсированы, и поэтому молекулы на поверхности

Жидкая

Ж/Ж

Эмульсии

обладают избытком свободной энергии

. Мерой этого избытка является поверхностное натяжение ,

Газообр

Г/Ж

Пена

газообразная

Тв.

Т/Г

Дым, пыль

т.е. свободная поверхностная энергия, приходящаяся на 1 см2 величины поверхности S. F S S .

жидкая

Ж/Г

Туман, кучевые

Избыток свободной энергии на поверхности делает систему термодинамически неравновесной. Поэтому все

5 Классификациядисперсныхсистемповзаимодействиюдисперснойфазыидисперсионнойсреды

Лиофильные системы, 1 фаза и среда близки по свойствам и хорошо взаимодействуют друг с другом, частицы

поверхностные процессы протекают самопроизвольно в сторону уменьшения F S , что достигается

сольватированы взаимодействуют с растворителем, 2 лиофильная система образуется самопроизвольно, 3 ∆F< 0 , 4

уменьшением S или .

система устойчива не нуждается в стабилизации, 5 обратимые, возможны переходы от истин р-ра к коллоидной и

наоборот, 6 σ<σкр, 7 растворы ВМС и ПАВ

Дисперсность. Количественный признак объектов коллоидной химии, он указывает на степень

Лиофобная система 1 нет взаимодействия с растворителем 2 Образуется принудительно с затратой энергии 3 ∆F>0, 4

раздробленности

или

величину межфазной

пов-ти. количественные

параметры раздробленности:

неустойчивая система нуждается в стабилизаторе, 5 Необратимы, 6 σ˃σкр, все остальные растворы кроме ВМС и

размер частиц

a ,

дисперсность

, удельная поверхность S.

В зависимости от формы

ПАВ

Классификациядисперсныхсистемповзаимодействиючастицдисперснойфазы.

Связанныедисперсистемы(частицысвязмеждусобойобразуютструктуругели)

6Свободныедисперсныесистемы(частицынесвязанымеждусобой, золи)

частицы берется ее характеристический размер: для сферы - диаметр d , для куба – ребро l. Для

7 Классификацияповерхностныхявлений

2-го начал

термодинамики позволяет

классифицировать

частиц неправильной формы в качестве количественной характеристики раздробленности

Объединенное

уравнение

1-го

применяется

удельная поверхность

S12 , к

единице

массы

;

м2 Для

S12

Sуд V

уд

кг

монодисперсной системы, содержащей n частиц сферической формы радиуса

r :

поверхностные явления. Запишем это уравнение в форме:

(5.4)

где G - энергия Гиббса, S- энтропия, T- температура, V- объем, P - давление, σ- поверхностное

S уд

4 r 2

- поверхность,

i -

химический потенциал, ni -

- электрический

натяжение,

число молей,

K , где K - коэффициент формы частицы

В общем случае

S уд

потенциал, q- заряд. Стрелкой 1 указан переход поверхностной энергии в энергию Гиббса. Такой переход

имеет место при адсорбции, а также лежит в основе изменения реакционной способности с изменением

Дисперсность или удельная поверхность является термодинамическим параметром состояния,

дисперсности. Стрелка 2 обозначает переход поверхностной энергии в теплоту, который происходит при

изменение которого вызывает изменение других равновесных свойств. система обладает

изотермической перегонке и адсорбции и выражается теплотой конденсации, смачивания или адсорбции.

дополнительной степенью свободы

F K Ф 3 .

Переход поверхностной энергии в механическую указан стрелкой 3. Такой переход наблюдается при

3 Классификациядисперсныхсистемпоразмерамчастицдисперснойфазы

адгезии, капиллярности, адсорбции. Стрелка 4 указывает на переход поверхностной энергии в химическую,

что соответствует таким поверхностным явлениям, как адсорбция, коррозия. Наконец, переход

поверхностной энергии в электрическую указан стрелкой 5. Такой переход приводит к образованию электрического

заряда поверхности и двойного электрического слоя и соответствует группе электрокинетических явлений: электрофорезу,

электросмосу, потенциалам течения и оседания.

8 Общие причины отличия состояния поверхностного слоя от объемных фаз. Изменение плотности свободной

энергиинаграницеразделавлиофобныхилиофильныхсистемах

f f 0 ,

Рассмотрим основные отличия свойств поверхностного слоя от свойств объемных фаз и

Когда

т.е.

для

лиофобных

систем, для

разнородных фаз при слабом их

причины этих отличий.

взаимодействии, избыток свободной энергии велик, заштрихованная площадь велика, но толщина

1. Первое отличие: внутренняя энергия слоя отличается от внутренней энергии объемных фаз,

межфазного слоя мала, т.к. молекулярные силы убывают с расстоянием, взаимодействие между фазами

т.

к.

каждой

фазе

взаимодействуют

молекулы

одного сорта,

а в

поверхностном слое

-10

отсутствует или оно мало. Для лиофобных систем толщина межфазного слоя составляет всего (1-10) 10

взаимодействуют разные молекулы.

м.

В лиофильных

системах фазы являются родственными,

они

сильно

взаимодействуют,

U s U

0 .

Значение межфазного поверхностного натяжения в лиофильных системах мало и

2. Взаимодействие молекул в поверхностном слое происходит в несимметричном силовом поле.

составляет величину m 0,1эрг/ см2 .

Равнодействующая межмолекулярных сил, действующая на молекулу, находящуюся в поверхностном

слое, не равна нулю. Поэтому молекулы стремятся уйти с поверхности в объем, и наоборот, при

Избыток свободной поверхностной энергии в таких системах меньше, заштрихованная площадь

увеличении поверхности происходит вывод молекул из объема на поверхность, при этом затрачивается

меньше.

работа против межмолекулярных сил dA dS . Эта работа равна увеличению свободной

Вследствие сильного взаимодействия фаз, проникновения молекулярного взаимодействия глубоко в объем

каждой фазы, толщина поверхностного слоя в лиофильных системах велика. Поверхностный слой более

поверхностном энергии F S . Таким образом, в поверхностно слое происходит сгущение, увеличение

размыт, имеет большую протяженность. По энергетическим параметрам он приближается к фазам

свободной поверхностной энергии dF S

0 , F S T ,Ui,V S . Следовательно,

плотность свободной энергии в объемных фазах и поверхностном слое различна.

Поверхностноенатяжение,егоопределенияиразмерности.

F S

ПН-

это обратимая изотермическая работа образования единицы поверхности,

T , ni

Рис.2.2. Межмолекулярные взаимодействия в объеме и на поверхности.

которая затрачивается

на преодоление сил межмолекулярного взаимодействия и переходит в

свободную поверхностную энергию.

ПН-частная производная от любой

Вследствие

избытка

свободной

поверхностной энергии

происходит

изменение

концентрации компонентов в поверхностном слое. Это изменение может быть как положительным,

s S ,V ,ni

s S ,P,ni

s T ,V ,ni

s T ,P,ni

так и отрицательным.

Состав поверхностного слоя отличается от состава объемных фаз

характеристической функции по площади межфазной поверхности при постоянных соответствующих

niS

ni ni . В поверхностном слое концентрируется компонент, уменьшающий избыток

параметрах.

свободной поверхностной энергии. 4. Значения энтропии поверхностного слоя и объемных фаз

ПН- это силанаправленная тангенсально к пов-ти приход-ся на 1-цу периметра огранич его поверхность и

стремящ-ся эту поверхность сократить.

различны

S S S

S . При контакте газа с жидкостью или твердым телом поверхностный

Единицы измерения поверхностного натяжения:

слой

разрыхлен. На

поверхности

жидкости

постоянно

протекают

процессы

испарения и

в Си

Дж

Н м

Н ,

в СГС

эрг

дин см

дин

-7

конденсации. Среднее время жизни молекулы воды на поверхности составляет 10

сек. Из-за

м2

см2

см

возможности выхода молекул в

менее плотную фазу их число степеней свободы увеличено,

поэтому

S . При

контакте жидкости с твердым телом

происходи ориентация молекул жидкости,

энтропия

уменьшается

S . Таким образом,

поверхностный слой характеризуется

избытком термодинамических свойств, который может быть как по-

ложительным, так и отрицательным.

http://www.mitht.org/forum/

МетодизбыточныхвеличинГиббса. ВыводфундаментальногоуравненияГиббсадлясвободнойэнергиисистемысплоской

11 ВыводфундаментальногоуравненияГиббсадлясвободнойэнергииплоскогоповерхностногослоя,егоанализ.

границейразделафаз.

Плоским поверхностным слоем называется такой слой, толщина которого много меньше радиуса

Гиббс предложил метод основанный на исключении неопределенного значения толщины

кривизны, т. е. система отвечает условию: R .

энергии

определяется

выражением

называетповерхностногоповерхностьюслоя. Он заменилразрывагетерогенную, понимая подсистемуэтимнанеоднородныйидельную, заменивтонкийповерхностныйслой, разделяющийслой на

Для

всей

системы

изменение

свободной

разделяющую поверхность, которая проводится внутри повех слоя.

Поверхностный слой

Гиббс

объемные фазы и обладающий конечной толщиной и объемом. Разделяющая поверхность –

dF dF

Согласно выражению,

полученному для системой с плоской границей

геометрическая поверхность, воспроизводящая форму поверхности разрыва и располагающаяся

параллельно ей. Разделяющая поверхность - фиктивная, воображаемая поверхность, на которой

раздела dF ds S dT p dV i

dni .

происходит разрыв непрерывности в плоскостях m, F , S,

состава.

1 фазы однородны на всем протяжении вплоть до раздел пов-ти

соответствии

методом

избыточных

величин

Гиббса

изменение

свободной

энергии

2 Каждая точка вещества на поверхности находится в одинаковых условиях.

dF S

dF dF

dF . Для каждой объемной фазы справедливо

3 Положение поверхности фиксируют, выбирая определенную величину адсорбции на поверхности

поверхностном слое равно

4 разность экстенсивной величины реал. И идеал сист дает некую избыточную величину,

выражение

Посредством этих избытков выражаются все экстенсивные параметры в методе Гиббса, поэтому этот метод

называется методом избыточных величин.

S dT p dV

dni

Минусы примен для сист Ж/Ж и Ж/Г, величина избытка завис от места где провести раздел. Пов-ть, свойства

слоя не рассматр.

5) dF

dT p dV

i dni

При этом совершается работа dA p dV ds Согласно первому закону термодинамики

В этих выражениях у i нет индекса, т.к. при равновесии значения химического потенциала в обеих фазах

dQ dU dA dU p dV ds .

Согласно

второму

закону

термодинамики при

выравниваются. Вычитая из выражения (3) выражения (4) и (5) и учитывая, что экстенсивные свойства

(V , S, ni , F )

суммируются и что при достижения равновесия i

i S

, получим

установлении

равновесия dQ T dS .

Объединим уравнения

первого

и второго

закона

dF S ds S S dT i dni S

термодинамики при установлении равновесия T dS dU p dV ds .

Свободная энергия поверхностного слоя складывается из трех членов: работы увеличения поверхности раздела фаз,

1) dU T dS p dV ds Перейдем от внутренней энергии к свободной

энтропийного члена, учитывающего изменение связанной энергии системы и члена, учитывающего вещественный

энергии, т.е. заменим U на F. U F T S

dU dF T dS S dT

обмен между фазами и поверхностным слоем, т.е. состав поверхностного слоя. СМ билет 9

Экспериментально доказано, что на границе жидкости или твердого тела с газом с

Объединим уравнения 1) и 2)

dF T dS S dT T dS p dV ds

T S, Ni

dF ds S dT p dV Это -

уравнение для закрытой гетерогенной системы с

повышением температуры поверхностное натяжение уменьшается, т.к. увеличивается расстояние между

плоской границей раздела. Для открытой системы учитывается вещественный обмен,

т.к.

число

молекулами и уменьшается межмолекулярное взаимодействие.

Химический

молекул в системе может изменяться, и уравнение принимает вид:

S,T,NJNi

3) dF ds S dT p dV i

dni

потенциал - это мольное приращение свободной энергии при постоянном объеме при переходе i-го

Это уравнение

отличается

от

уравнения

для

гомогенной

системы

членом

ds ,

компонента в поверхностный слой. Химический потенциал характеризует скорость, с которой меняется

свободная энергия при изменении концентрации данного вещества.

обозначающим работу образования поверхности. Из этого уравнения видно, что с увеличением

поверхности увеличивается свободная поверхностная энергия. При увеличении числа компонентов

также происходит увеличение свободной поверхностной энергии.

12 Понятиеобадсорбции.Причиныадсорбции.Количественныехарактеристикиадсорбции

0 и Гi 0 . При таком

можноопредкакпроцесс выравниванияхим-хпотенциалов компонентовмеждуповерхностью иобъемом, приводящийкизменению

Гиббс показал, что разделяющую поверхность

можно

провести так чтобы

концентрациинаповерхности

выборе

разделяющей

поверхности

можно

считать,

что

адсорбция

растворителя

отсутствует

адсорбция–этоизменениеконцв-вавповерхностномслоепосравнениюегоконнцвобъеме

d Г d .

адс-ция–этосгущениегазообразногоилирастворенногов-ванапов-ти

причиныадсорбциистремленсистемыуменьшениесвободнойпов-тнойэнергии,этозначитперераспределениекомпонентов ивыводна

пов-тьтогокомпанентакоторыйснижаетпов-тноенатяжения

Перейдем к концентрации.

R T ln a R T ln C , где

С –

равновесная концентрация в

Колич.Характеристики

Избыточнаяконцi-огокомпанентарассчитаннаяна1-цуплощадиразделяющейпов-ти

моль

объеме. d R T ln C

;

dC;

d Г R T

R T

S м2

гиббсова адсорбция поверхностная концентрация адсорбата , равная общей концентрации

Из этого уравнения видно, что для ПАВ величина адсорбции растет с увеличением

концентрации

вещества в поверхностном слое и выражаемая в

моль .

При малых концентрациях адсорбата

понижением

температуры.

Величину

называют

поверхностной

активностью

м 2

Гi и

совпадают, при больших -

различаются. Когда поверхность адсорбента неизвестна,

C 0

обозначают символом g в честь Гиббса. Единицей измерения поверхностной активности служит 1 Гиббс.

величину адсорбции измеряют емкостью поверхностного слоя A и выражают в

моль . Это также

Проведем анализ уравнения Гиббса. Если

, то Г 0, что характерно для ПИАВ,

проявляющих

кг

общее количество вещества в поверхностном слое, используется когда не знаем площадь пов-ти

13 ВыводадсорбционногоуравненияГиббсадляразбавленныхрастворов,егоанализ.

отрицательную адсорбцию.

d Гi d i

Если

то

Г 0 ,

что

характерно

для

ПАВ,

проявляющих положительную

Для бинарной системы:

d Г1

d 1 Г2 d 2 ;

где индекс 1 относится к растворителю, 2 – к растворенному веществу. Изменение связано с

адсорбцию.

Если

, то

Г 0,

что характерно для неактивных веществ.

адсорбцией и с изменением концентрации растворителя и растворенного; вещества. Это уравнение содержит

два неизвестных,

Г1 ,

Г2 и поэтому однозначное его решение отсутствует. Один из путей его решения

Используя уравнение Гиббса, можно найти величину адсорбции Г для любого значения С, из тангенса угла наклона

следующий. Величины адсорбции зависят от положения разделяющей поверхности. В зависимости от выбора

касательной к экспериментальной кривой

С . Таким путем можно перейти от изотермы поверхностного

натяжения к изотерме адсорбции

положения разделяющей поверхности адсорбция первого компонента оказывается положительной,

отрицательной или равной нулю.

Существует два способа графического решения уравнения ЛенгмюраПо

14ПоверхностнаяактивностьпоРебиндеру.Графическоеопределениеповерхностной

активности.

первому

способу по

изотерме находят

значение

. Затем

продолжают

max

1 - ПАВ. Г 0 ;

0 .

начальный прямолинейный участок изотермы до пересечения с линией max

и из точки пересечения опускают перпендикуляр до точки

p' на оси абсцисс.

2 - неактивные вещества Г 0;

При малых p значение K

p 1, и им знаменателе можно пренебречь. Тогда

уравнение принимаетвид: max K p'. При max

K p' 1.Отсюда K

3 - ПИВ.

Г 0 ;

Второй способ решения уравнения Ленгмюра применяется, когда экспериментальная изотерма не

имеет третьего линейного участка, т. е. значение

неизвестно. Уравнение преобразуется в уравнение

max

прямой:

;

g = -

= RT (Г/С) пов-тная активность по Ребиндеру измер в [Гиббс] физический смысл – эта

1 Kp

max K

max

max Kp

max

C 0

. Решение уравнения Ленгмюра

; max

ctg

сила удерживающая в-во на пов-ти и расчит-ая на 1-цу Гиббсовой адсорбции можно опред графически tgα = g

15 Сталагмометрический и тензиометрический методы

исследования

поверхностного

m ax

натяжения

16 Переход от изотермы поверхностного натяжения к изотерме адсорбции графическим методом, расчетвеличиныГmахспомощьюуравненияЛенгмюра.

При малых значениях p всегда можно подобрать такое значение p, когда значение K p 1, и уравнение Ленгмюра принимает вид:

max K p ,

То есть пропорциональна p, что соответствует начальному линейному участку кривой. При больших значениях p можно подобрать такие значения p, когда величина K p 1 и

max , что соответствует третьему участку изотермы. Второй криволинейный участок изотермы описывается полным уравнением Ленгмюра. Таким образом, это уравнение хорошо

описывает всю изотерму адсорбции, в отличие от уравнения Фрейндлиха.

http://www.mitht.org/forum/

17 ВлияниенаадсорбциюнаграницерастворгазстроенияиразмерамолекулПАВ.Правило

19 Построение изотермы адсорбции по изотерме поверхностного натяжения расчетным путем с

Траубе,егоаналитическоевыражениеифизическоеобоснование

помощьюуравненияШишковского.СвязьмеждуконстантамиуравненияШишковскогоиЛенгмюра.

В гомогенном ряду олифатических соединений при увеличении длины радикалов.

на 1 группу СН2

На изотерме поверхностного натяжения имеются три участка (рис. 4.15).

поверхностная активность g

увеличивается в 3,2 раза это правило справедливо для разбавленных водных

растворов комнатной температуры (dσ/dc)n+1/(dσ/dc)n=3,2

Рис. 4.15

K n 1

3 , 2

Первый и третий участок - прямолинейные, а второй характеризуется логарифмической

зависимостью

σ от

С. Для

этого участка

польский

ученый

Шишковский

в 1908 г.

K n

предложил эмпирическое уравнение:

При увеличении длинны радикала ухудшается растворимость

A R T

lnK

Работа адсорбции, работа

C - концентрация ПАВ,

1 - удельная капиллярная постоянная, характерная для

по переносу 1 моля в-ва в пов-ный слой

An 1 An R T lnKn 1

R T lnKn

0 B ln(

R T ln

Kn 1

2 3002,3 0,5 690кал/ мол

A 1)

каждого ПАВ, В- константа, мало зависящая от природы ПАВ.

Физический смысл правила: работа адсорбции на 1 группу постоянна = 690 кал/моль

При малых С:

ln(C

18 УравнениеШишковского,связьсегопомощьюуравненийЛенгмюраиГиббса

Выше говорилось о том, что уравнение Шишковского является эмпирическим. После разработки

по формуле разложения в ряд и уравнение принимает вид:

представлений о мономолекулярной адсорбции Ленгмюр теоретически получил уравнение, носящее его имя:

Г Гmax

K C

(1)

B A

K C

т. е. описывает

первый прямолинейный участок.

После дифференцирования: d 0

dC ;

Оказалось возможным получить уравнение на основе уравнений Ленгмюра и Гиббса. Запишем уравнение

Гиббса.

(2) Приравниваем уравнения (1) и (2) –

Гmax

K C

B ,т. е. можно определить поверхностную активность.

R T dC

1 K C

Разделим переменные и проинтегрируем:

;

0 Гmax R T ln(1 K C)

Для определения

констант

уравнения

Шишковского

рассмотрим

второй участок

изотермы

поверхностного

K dC

натяжения.

При

больших

можно

пренебречь

единицей,

тогда

d Гmax R T

0 0 B ln

K C

Сравнивая с уравнением Шишковского, видим, что

Это

уравнение

прямой линии

в координатах

ln C (рис.

4.16).

Гmax R T 0 B ,

0 0 B ln

C - концентрация ПАВ, 1

Рис. 4.16. Определение констант уравнения Шишковского.

- удельная капиллярная постоянная, характерная для каждого ПАВ,

Из этого рисунка видно, что tg 0 B При 0 :

- константа, мало зависящая от природы ПАВ.

0 B ln

;

ln C ln

1 ,т. е. отрезок, отсекаемый прямой линией на линии 0

равен

1 .

Таким образом, уравнения, описывающие изотермы адсорбции и поверхностного натяжения,

взаимосвязаны между собой. Определив константы уравнения поверхностного натяжения, можно

Сравнивая с уравнением Шишковского, видим, что Гmax R T 0

B ,

определить константы уравнения Ленгмюра.

Таким образом, уравнения, описывающие изотермы адсорбции и поверхностного натяжения, взаимосвязаны между

собой. Определив константы уравнения поверхностного натяжения, можно определить константы уравнения

Ленгмюра

Строениеадсорбционныхпленокнажидкойповерхности. Диаграммысостоянияповерхностных

21 Выводуравнениесостояниядвухмерногогаза.УравнениеФрумкинадляреальногодвухмерногогаза

пленок.

В двумерном газе действует поверхностное давление, которое является растягивающим, в противоположность

Фазовое состояние поверхностных пленок описывается диаграммой состояния или изотермой сжатия,

поверхностному натяжению, сжимающему

поверхность.

Это давление равно

. При малом

которая может быть построена в координатах sм .

содержании ПАВ, т.е. в состоянии двумерного газа 0 K C . После дифференцирования получим:

Поверхностное давление измеряют непосредственно с помощью весов Ленгмюра. Этот метод основан на

d d K dC (1)

прямом измерении горизонтальной силы, которая действует на поплавок, отделяющий пленку от

поверхности чистого растворителя. Современные весы позволяют определять поверхностные давления с

точностью до сотых долей дины на см. В общем случае при уменьшении площади реализуются

Подставим уравнение (1) в уравнение Гиббса:

газообразное, жидкое и твердое состояние монослоя. Каждое состояние монослоя характеризуется

определенной ориентацией молекул, зависящей от sм , адгезионных и когезионных свойств систем. В

C K

диапазоне давления и площади, занимаемой 1 молем ПАВ, отвечающем всем трем агрегатным состояниям

R T

пленки, диаграмма состояния имеет вид, показанный на рисунке 4.7.

sм . Тогда

Площадь, занимаемую одним молем ПАВ, обозначим через

;

; sм

R T .Это уравнение состояния двумерного газа аналогично уравнению газа

sм

R T

sм

P V R T .

Для реального двумерного газа справедливо уравнение Фрумкина, аналогичное уравнению Ван-дер Ваальса:

Рис. 4.7. Диаграмма состояния поверхностных пленок.

(

(sм ) R T

Участок a соответствует двумерному газу и аналогичен кривой сжатия газа. На участке b

)

sм2

где - константа взаимодействия молекул ПАВ в поверхностном слое,

- эффективная площадь сечения

происходит конденсация. В этом состоянии пленка называется растянутой жидкой пленкой и способна к

сжатию, которому соответствует участок c . На участке d происходит фазовый переход, участку e

молекулы.

соответствует конденсированная (твердая) пленка. Участку

соответствует разрушение

.22 Адсорбциянаграницетвердоетело–газ.ТеориямономолекулярнойадсорбцииЛенгмюра.Выводи

мономолекулярной пленки, т. е. образование капли для жидкой пленки или многослойных образований для

анализуравненияизотермымономолекулярнойадсорбцииЛенгмюра

твердой пленки. Поверхностные пленки реальных ПАВ описываются диаграммами состояния,

Теория Ленгмюра учитывает ограниченность поверхности адсорбента, что приводит к

отвечающими определенному участку общей диаграммы состояния. Это зависит от длины углеводородного

адсорбционному насыщению поверхности по мере увеличения концентрации адсорбата.

радикала молекулы ПАВ. Так, лауриновая кислота C11 H 23COOH благодаря

При разработке этой теории Ленгмюром были сделаны следующие допущения:

Адсорбция локализована, адсорбционные силы близки к химическим.

Адсорбция происходит на активных центрах адсорбента, которые энергетически

сравнительно короткому радикалу образует только газообразные пленки (кривые 1, 2, 3, рис.4.8).

эквивалентны.

Радиус действия адсорбционных сил мал, и один активный центр адсорбирует одну молекулу

адсорбата, причем образуется мономолекулярный адсорбционный слой.

Рис.7

Устанавливается динамическое равновесие адсорбция десорбция.

Между адсорбированными молекулами отсутствует взаимодействие, вследствие чего время

Рис. 4.8. Диаграммы состояния поверхностных пленок лауриновой (1),

пребывания на поверхности не зависит от того, занят соседний активный центр или нет.

миристиновой (2) и пальмитиновой (3) кислот.

Вывод уравнения Ленгмюра.

Миристиновая кислота C13 H 27 COOH образует как газообразные, так и конденсированные пленки.

Ленгмюр рассматривал адсорбцию как квазихимическую реакцию между газом и активными

Пальмитиновая кислота C15 H31COOH при обычной температуре образует только конденсированные

центрами с образованием адсорбционного комплекса.

Обозначим давление газа через p , концентрацию свободных активных центров через

0 ,

пленки вследствие большой длины углеводородного радикала.

концентрацию занятых активных центров через . Тогда константа равновесия K

p O

K p O ; O max ; K p max

K p max k P ; K p K p max

1 Kp K p max ; K p max

1 K p

Очевидно, величина равна поверхностной концентрации адсорбата, т. е. количеству адсорбированного вещества а, т.к. один активный центр занимает одна молекула адсорбата.

http://www.mitht.org/forum/

K p amax ; Иногда числитель и знаменатель этого выражения делят на

K .

точки p'

на оси абсцисс. При малых p

значение

K p 1,

и им знаменателе можно пренебречь. Тогда

уравнение принимаетвид: max K p'. При max

K p' 1.Отсюда K

1 K p

. Константы уравнения Ленгмюра имеют следующий

a a max

a max

Второй способ решения уравнения Ленгмюра применяется, когда экспериментальная изотерма не

A p

имеет третьего линейного участка, т. е. значение max

неизвестно. Уравнение преобразуется в уравнение

смысл.

прямой:

;

- это максимальная адсорбция при образовании мономолекулярного слоя, т. е.

1 Kp

max

K - константа адсорбционного равновесия, связанная с теплотой

max Kp

max

max K

max

емкость монослоя.

. Решение уравнения Ленгмюра

; max

ctg

адсорбции. К характеризует энергию взаимодействия адсорбата с адсорбентом, т. е. химическое

сродство. Для любой химической реакции справедливо выражение

m ax

G R T ln K ;

G H T S ;

H Q ;

K e

H T S

e S R eQ R T g eQ R T

R T

23 ЛинейнаяформауравненияЛенгмюра.НахождениеконстантуравненияЛенгмюраграфическим

Анализ уравнения Ленгмюра

методом.Определениеудельнойповерхностиадсорбента

константа равновесия

На изотерме адсорбции, изображенной на рис. 3.10 можно выделить три участка. При малых

p O

значениях

p всегда можно подобрать такое значение

p , когда значение

K p 1, и

Уравнение Ленгмюра позволяет определить удельную поверхность адсорбента.

уравнение Ленгмюра принимает вид: max K p ,

То есть пропорциональна

p , что соответствует начальному

Действительно, произведение

max Na

равно

числу молекул,

приходящихся

на

см поверхности.

линейному участку кривой.

При больших значениях

p можно

Умножив это значение

на площадь,

занимаемую одной молекулой

получим

величину удельной

поверхности Sуд max Na S0 .

подобрать такие значения

p , когда величина

K p 1 и

max , что соответствует третьему участку изотермы. Второй

Рис. 3.16. Изотерма полимолекулярной адсорбции.

криволинейный участок изотермы описывается полным уравнением Ленгмюра. Таким образом,

это уравнение хорошо

описывает всю

изотерму

адсорбции,

в отличие

от

уравнения

Часто

изотермы

адсорбции имеют

вид,

отличающийся от

ФрейндлихаСуществует два способа графического решения уравнения ЛенгмюраПо первому способу по

S -образный вид (Рис. 3.16). Это

изотерме находят значение

max . Затем продолжают начальный прямолинейный участок изотермы до

ленгмюровской изотермы,

а именно

пересечения с линией

и из точки пересечения опускают перпендикуляр до

объясняется полимолекулярной адсорбцией, или капиллярной

max

конденсацией. Изотермы адсорбции полимеров, как правило, не являются

ленгмюровскими, т. к. одна макромолекула занимает несколько активных центров адсорбента, т. е.

предпосылки, положенные в основу уравнения Ленгмюра, не соблюдаются.

24 Адсорбциякакобратимыйэкзотермическийпроцесс.Интегральнаяидифференциальная

Дифференциальная теплота адсорбции - это тепло, выделившееся при дополнительной адсорбции

теплотаадсорбции

малого количества адсорбата в расчете на моль адсорбата

qдиф

Дж

В адсорбционном слое молекулы газа способны к перемещению лишь в двух

измерениях,

поэтому адсорбция газа сопровождается уменьшением энтропии,

т.е.

S 0 .

кг адсорбента

Условием протекания адсорбции как самопроизвольного процесса является уменьшение энергии

Дифференциальная теплота адсорбции характеризует не весь адсорбционный процесс, а некоторую его

a . Дифференциальная теплота адсорбции с

Гиббса, т.

е.

G 0 . Из

термодинамической зависимости

G H T S

стадию, для которой адсорбция достигла величины

следует, что теплота адсорбции должна быть отрицательной, т. е. адсорбция газов или паров на

увеличением количества адсорбированного вещества уменьшается (рис. 3.2).

твердом теле всегда является экзотермическим процессом. Теплота адсорбции может быть

определена прямым калориметрическим методом и рассчитана из обратимой изотермы

адсорбции по уравнению Менделеева-Клаузиуса-Клайперона

дln P

адс

дT

Причиной выделения тепла при адсорбции является уменьшение энергии поверхности

25 Сравнительнаяхарактеристикафизическойадсорбцииихемосорбции

физическаяадсция (адсорбционныесилымежмолекулярныеВандервальса,2)неспецифична,т.е.наодноитожеввоможетпримерно

адсорбента.

одинаковоадсорбироватьсянаразныхповерхностях,наиболееважнуюрольиграетплощадьповти 3)можетбытьмонослойнойи

полислойной4)обратима5)теплотамала28ккал/моль6)сувеличениемтемперадсуменьшается7)нелокализована,м.б.локализована

принизкихтемпературах

хемосорбцияилихимическаяадсорбция(любоехимическоевоздействие 2)специфична,тольконаопределеннойповти,энергетический

фактор,есливпроцессеадсорбции∆Gуменьшаетсяадсцияможетпройтивслучаеувеличениясвободнойповерхностнойэнергии 3)всегда

монослойна4)необратима5)теплотазначительнобольшеот10100ккал/моль 6)сувеличениемтемпературыхимадсцияувеличивается,

т.к.требуетсязначительнаяэнергияактивации7)локализована

Рис. 3.1. Зависимость теплоты адсорбции от величины адсорбции.

Различают дифференциальную и интегральную теплоту адсорбции. Интегральная теплота

адсорбции - это общее количество тепла, выделившееся при адсорбции данного количества

адсорбата на 1 кг адсорбента q

инт

Q Дж ;

инт

Дж

s м2

кг адсорбента

Зависимость интегральной теплоты адсорбции от величины адсорбции нелинейна (рис. 3.1), т. к.

поверхность адсорбента энергетически неоднородна.

кривыепотенциальнойэнергиидляфизическойадсорбцииихемосорбции.

Адсорбент

Адсорбат

Силы взаимодействия

Кривые потенциальной энергии при адсорбции двухатомного газа X 2

на металле М

полярный

ориентационные

полярный

неполярный

индукционные

неполярный

полярный

неполярный

дисперсионные

Дисперсионные силы проявляются между мгновенными диполями, возникающими при сближении молекул за

счет флуктуаций электронной плотности. Резонанс таких флуктуаций приводит к уменьшению общей энергии

системы, обусловленному притяжением атомов. Потенциал межмолекулярного взаимодействия

определяется выражением: U межмол.взаим.

U ор U инд

U дисп

Полная энергия адсорбционного взаимодействия определяется уравнением Леннард-Джонса

B , где C - константа межмолекулярного притяжения, B- константа борновского

r 6

r12

C - энергия межмолекулярного

отталкивания, происходящего при перекрывании электронных орбит,

r 6

(дисперсионного) притяжения,

B - энергия борновского отталкивания, которое происходит при малых r и

r12

обусловлено запретом Паули. Межмолекулярные силы действуют на малых расстояниях порядка 10-9 м.

Кривая (1) описывает изменения энергии физического взаимодействия между металлом

28 ТеорияполимолекулярнойадсорбцииБЭТ,предпосылкитеории.Уравнениеизотермыадсорбции

БЭТ,егоанализ

M и газом X 2 . Она включает в себя Вандер-Ваальсовы (диполь-дипольные и лондоновские)

на поверхности адсорбента имеются активные центры, и взаимодействием между молекулами адсорбата в

силы притяжения и борновские силы отталкивания.

слое пренебрегают. По теории БЭТ считается что активн центры на пов-ти адсорбируется 1 молекула и эта

молекула сама становится активным центром, т.о. молекулы первого адс-ого слоя являются активными

Кривые (2) и (3) описывают хемосорбцию, в которой молекула адсорбата в начале

центарми для второго и тд. Теплота адсорбции первого слоя есть теплота адсорбции Qад , а теплоты

диссоциирует на 2 атома X .

Поэтому для протекания хемосорбции необходимо затратить

энергию, равную энергии диссоциации. Величина этой энергии показана на больших расстояниях

адсорбции всех последующих слоев одинаковы и равны теплоте объемной конденсации L Q .

от поверхности. Кривые (2) и (3) характеризуются относительно глубоким минимумом,

ад

соответствующим теплоте хемосорбции и находящемся на более близком расстоянии от твердой

Можно показать,

что в этом случае константа равновесия адсорбции выражается уравнением

поверхности, чем относительно мелкий минимум на кривой физической адсорбции.

Qa L , где

- константа равновесия образования единичного адсорбционного комплекса,

Как правило начин как физичекая адс-ция по кривой 1 не треб затрат на начальной стадии м.б. переход от

g' e

физич адс к химической адс. Без затрат энергии, по мере заполнения пов-ти для перехода треб-ся энергия

активации и в этом случае адс-ция называется активированной хемосорбцией. Если энергетический барьер

= энергии активации по величине. А скорость адс-ции не велика, то процесс идет как физическая

KL - константа равновесия образования всех последующих комплексов, Qa L - чистая теплота адсорбции.

адсорбция.

27 Природаадсорбционныхсил.УравнениеЛеннард–Джонса

Уравнение изотермы адсорбции в теории БЭТ имеет вид:

Физическая адсорбция происходит под действием Ван-дер Ваальсовых сил

max C

, где max

- емкость монослоя, p i

- давление насыщенного пара при

межмолекулярного взаимодействия, которое складывается из ориентационных, индукционных и

дисперсионных сил.

1 p pi 1 C 1 p pi

данной температуре. Уравнение () описывает всю изотерму полимолекулярной адсорбции

http://www.mitht.org/forum/

Для решения уравнения БЭТ его приводят к линейной форме:

Кинетика адсорбции. Динамическое уравнение адсорбции. Уравнение Френкеля. Кинетические кривые

адсорбцииприразныхтемпературах.

C 1

| :

Кинетика адсорбции подчиняется уравнению первого

порядка. Чем больше насыщение поверхности, т. е. меньше

max C p

разность ( a at ), тем меньше скорость адсорбции.

Кинетические закономерности адс-ции опред скорость

установления

адс-ционного равновесия или скорости адс-ции. Чем

дольше времени молекула находится на пов-ти тем дольше уст-ся

1 C 1

адс-ционное равновесие

max C

k aравн аt

и почленно делят числитель на

С повышением температуры скорость адсорбции увеличивается, а равновесная адсорбция уменьшается

знаменатель

C 1 p

Константа

зависит

от теплоты

адсорбции, температуры

и коэффициента диффузии адсорбата.

max

C 1

Температурный коэффициент адсорбции мал, т. к. энергия активации физической адсорбции равна 0.

Динамическое уравнение адсорбции Г=nτ n-число молекулярных столкновений с пов-тью в 1 момет времени, t –

время жизни молекулы на пов-ти

max C

Уравнение которое связывает время прибывания мол-лы на пов-ти с теплотой адс-ции и температурой предложил

29 Линейнаяформа уравненияБЭТ. Нахождениеконстант уравненияБЭТграфическимметодом.

Френкель

o eqa RT

Определениеудельнойповерхностиадсорбента.

По теории БЭТ легко найти удельную поверхность адсорбента уд max Na S0 ,

где

- константа, равная периоду колебаний в решетке адсорбента порядка 10 13 сек . Как видно

- площадь, занимаемая одной молекулой адсорбата. См 28

из уравнения, сильно зависит от Т и qa (молярная теплота адс-ции), т. к. они стоят в показателе

степени.

31 Смачивание.Краевойуголитеплотасмачивания.УравненияЮнга.ВлияниеПАВна

32 Когезияиадгезия.Характерразрушенияадгезионногосоединения.Условиеадгезионного

смачивание

разрушения.УравнениеДюпредляработыадгезии

Под смачиванием понимают совокупность поверхностных явлений, происходящих на границе

Когезией называют явление сцепления молекул в объеме однородного тела. Чтобы установить связь

раздела трех контактирующих фаз

поверхностной энергии с энергией межмолекулярного взаимодействия в объеме, вводят величину,

Оно зависит от взаимодествия молекул в объеме каждой фазы и между фазами и сопровождается убылью

называемую работой когезии

. Работа когезии - это обратимая изотермическая работа разрушения

энергий, при смачивании рассматриваются системы т-ж-г или Т-Ж-Ж в последненм случае смаличвание

называют избирательным

Располагаясь на пов-ти капля

столбика жидкости с сечением, равным единице.

жидкости образует с пов-тью угол, кот

Адгезией называют явление взаимодействия двух разнородных конденсированных фаз, состоящее в

называется каевой угол и обозначается

приведении их в контакт и в образовании связей между ними за счет сил притяжения. Одна из фаз

ϴ . Капля жидкости на

называется субстратом, другая – адгезивом (полимеры, т.к. они сочетают высокую липкость и прочность,

позволяющую передавать нагрузки от одного субстрата к другому) Существуют два подхода к рассмотрению

поверхности твёрдого тела.а) –

явления адгезии: механический и термодинамический. Согласно механическому подходу, количественной

смачивание,б) - несмачивание,в) -

характеристикой адгезионного соединения является адгезионная прочность, т. е. напряжение, необходимое

идеальное несмачивание.

для разрушения адгезионного соединения, разделения его на компоненты:

Pадс

F , где F - значение

Краевой угол всегда измеряют со стороны жидкости, а при контакте твердого тела и двух

жидкостей - со стороны более полярной фазы. Если 900 , то говорят, что твердое тело

силы при разрушении, S- площадь контакта.

смачивается жидкостью. При полном смачивании капля растекается на поверхности до

Работа разрушения адгезионнoгo соединения складывается

из работы адгезии и работы, затрачиваемой на деформацию:

образования мономолекулярной пленки и 00 . Если 900 , то жидкость не смачивает

Wразгр

Wадг

Wдеф

твердое тело. В случае полного несмачивания капля жидкости имела бы сферическую форму,

Работа деформации несоизмеримо выше работы адгезии, поэтому энергия межфазного разрушения на

если бы не действовала сила тяжести и 1800 . Полное несмачивание реализуется лишь в

условиях невесомости.

несколько порядков выше энергии адгезионных сил.

Условие адгезионного разрушения можно записать в

Поверхностная энергия твердого тела стремится уменьшится, что приводит к растеканию

виде: P

, где

Pадг

F / s

/ s ;

- значения силы при адгезионном и

капли по поверхности. Эта энергия равна поверхностному натяжению твердого тела на границе с

газом

. Межфазная энергия на границе твердого тела с жидкостью

адг

ког

тж

стремится сжать

когезионном разрушении образца, S- площадь контакта.

тг

Согласно термодинамическому подходу, количественной характеристикой адгезионного соединения

каплю, т.к. уменьшение площади поверхности приводит к уменьшению поверхностной энергии.

является работа

адгезии

Работа

адгезии определяется

как

обратимая

изотермическая работа

Когезионные силы,

действующие внутри капли,

также препятствуют растеканию.

Их действие

разделения двух конденсированных фаз вдоль межфазной поверхности, равной единице.

направлено по касательной к поверхности и равно

жг

. В условиях равновесия, когда капля

Определение работы адгезии может быть дано в терминах свободной энергии. Согласно этому

определению, работа адгезии - это свободная энергия равновесного обратимого разделения фаз на

жидкости перестает растекаться, силы поверхностного натяжения уравновешивают друг друга

бесконечно большое расстояние в изобарно-изотермических условиях. WA тг жг тж

(рис. 5.1

а). Условие равновесия выражается уравнением Юнга: тг тж жг cos

Это выражение для работы адгезии известно как уравнение Дюпре. Оно отражает закон сохранения

Решив это уравнение относительно cos , получим:

энергии при адгезионном расслаивании. Из него следует, что работа адгезии тем больше, чем больше

поверхностное натяжение исходных компонентов, взятых для образования адгезионного соединения, и чем

Поскольку

межфазные натяжения

на границе

с твердым телом

не

всегда

возможно

меньше конечное

межфазное

натяжение

в адгезионном

соединении. Работа адгезии характеризует

родственность контактирующих фаз, т е. степень насыщения нескомпенсированных поверхностных сил при

определить экспериментально, то уравнение Юнга чаще используется для решения обратной

контакте.

задачи смачивания, т.е. определения разности межфазных энергий по измеренным величинам

краевого угла.

ПАВ снижает пов-тное натяжение и тем самым улучшает смачивание

При рассмотрении адс-ции на границе р-р/ТВ тело необходимо учитывать взаимодействие адсорбента и

среды. Это взаимодействие хар-ся теплотой смачивания. ТС – измен энтальпии при взаимодействии ж-ти с

пов-тью другой ж-ти или твердого тела. Если ТС>ТА пройдет смачивание, если ТС<ТА пройдет адсорбция,

при увеличении ТС адсорбция уменьшается, т.к. пов-ть адс-та занимает растворитель

Условиерастеканияжидкостей.КоэффициентрастеканияпоГаркинсу.ЭффектМарангони

34 Связьадгезииисмачивания.ВыводуравненияДюпреЮнга,егоанализ

Условие самопроизвольного смачивания, или растекания жидкости,

которое выполняется

уравнением Юнга:

при значении 00 и

cos 1, можно записать в виде неравенства:

тг

тж

жг

тг тж жг cos

Подставим в уравнение Дюпре уравнение Юнга:

или тг тж

жг . Из уравнения Дюпре следует, что

тг тж

WA жг .

WA жг тг тж жг жг cos жг (1 cos )

Следовательно WA жг

жг или WA 2 жг ,

т. е. WA

Wk . Разность между правой

и левой частями неравенств, характеризующих растекание, называется коэффициентом

Ранее мы отмечали, что Wk

2 жг

растекания по Гаркинсу:

тг тж жг

f WA Wk

Поделив правую часть уравнения Дюпре - Юнга на 2 жг , получим отношение работ адгезии и когезии:

если f>0 то жидкость растекается по пов-ти ТВ. Тела

если f<0 то ж-ть не растекается

1 cos

При растекании жидкости с малым поверхностным натяжением по поверхности жидкости с большим

поверхностным натяжением проявляется эффект Марангони, т. е. течение жидкости под действием

градиента поверхностного натяжения, возникающего из-за локальных неоднородностей состава и

температуры в разных участках межфазной поверхности. Жидкость течёт из области малых в область

больших поверхностных натяжений вследствие самопроизвольного уменьшения поверхностной энергии

Проанализируем

полученное

выражение.

При

cos 1, WA

Wk , что соответствует

Гиббса. При ньютоновском течении напряжение сдвига

P пропорционально градиенту поверхностного

натяжения d / dx , где

x - расстояние в направлении движения жидкости,

P d / dx . Для

смачиванию

твердого тела жидкостью. При 1800

cos 1,

WA 0 ,

что соответствует полному

раствора ПАВ градиент поверхностного натяжения можно разложить на два множителя:

несмачиванию жидкостью твердого тела.

d d dc , dx dc dx

где первый множитель - поверхностная активность, а второй - градиент концентрации.

http://www.mitht.org/forum/

35 Межфазноенатяжениенаграницемеждувзаимнонасыщеннымижидкостями.Правило

показаны изотермы адсорбции жирных кислот из водных растворов на угле (а) и из толуольных

Антонова

растворов на силикагеле (б)

Для двух жидкостей с высокой точностью соблюдается правило Антонова, полученное

эмпирическим путем. Согласно этому правилу удельная межфазная энергия

равна разности

между поверхностными натяжениями более полярной

и менее полярной

жидкостей.

Межфазное натяжение равно раз-ти пов-х натяжения более и менее полярн жидкости

1 2

Для взаимно растворимых жидкостей величины

и 2

относятся

насыщенным

растворам.

Рис. 5.4. Изотерма адсорбции жирных кислот:а) из водных растворов на угле,б) из толуольных

Сопоставление выражения для работы адгезии с правилом Антонова приводит к

растворов на силикагеле.

следующему результату:

WA 1 2 1 2 2 2 Wk (2)

Правило выравнивания полярностей Ребиндера определяет условия выбора того или иного адсорбента

и структуру поверхностного слоя. Оно заключается в том что процесс адсорбции идет в сторону выравни-

т.е. работа адгезии в этом случае равна работе когезии менее полярной жидкости. Нарушение

вания полярностей фаз и тем сильнее, чем больше первоначальная разность полярностей. Растворенное

контакта жидкостей происходит по менее полярной фазе, взаимодействие в которой слабее, чем

вещество обладает обычно промежуточной полярностью и способностью скомпенсировать существующий на

в полярной, т.е. наблюдается когезионный характер разрушения. На более полярной фазе

границе раздела скачок полярностей двух разнородных веществ. При выполнении этого условия

остается адсорбированный слой менее полярной фазы.

уменьшается межфазное натяжение и свободная поверхностная энергия, что и является причиной

36 Адсорбциянаграницеразделатвердоетелораствор.ОбращениеправилаТраубе.При

адсорбции.

адсорбцииизводныхиуглеводородныхрастворов.Правилоуравниванияполярностей

диэлектрическая проницаемость ε

Ребиндера

сродство к среде увеличвается

Классификация видов адсорбции

этом случае

проводится

по адсорбату. Различают

ε а< ε с < ε в

молекулярную адсорбцию, т.е. адсорбцию неэлектролитов и ионную адсорбцию, т.е. адсорбцию

электролитов. При молекулярной адсорбции адсорбируются молекулы, при ионной - ионы,

адсорбция которых приводит к образованию двойного электрического слоя.

ε а> ε с >ε в

В адсорбции из раствора на поверхности твердого тела участвуют все три компонента. Этот вид

адсорбции является адсорбцией из смеси.

Обращение

При рассмотрении адс-ции на границе р-р/ТВ тело необходимо учитывать взаимодействие адсорбента и

среды. Это взаимодействие хар-ся теплотой смачивания. ТС – измен энтальпии при взаимодействии ж-ти с

пов-тью другой ж-ти или твердого тела. Если ТС>ТА пройдет смачивание, если ТС<ТА пройдет адсорбция,

при увеличении ТС адсорбция уменьшается, т.к. пов-ть адс-та занимает растворитель. Правило обращается

на мелкопористый адс-те с увеличением длины радикала молекула укрупняется и мелкие поры для нее

недостаточны. Часть пор выпадает из процесса адс-ции следовательно величина адс-ции уменьшается.

37 Ионнаяадсорбция.Влияниерадиусаивалентностиионовнавеличинуадсорбции

Неионогенные ПАВ являются растворимыми как в кислой так и в щелочной среде соединениями, не диссоциирующими

ИА

в воде. К ним относятся продукты присоединения окиси этилена к веществам с развитыми углеводородными

радикалами: оксиэтилированные спирты

Сn H 2n 1 O (CH 2 CH 2 O )m H

n 10 18

Ионы способные поляризоваться адс-ся только на пов-ти состоящих из полярных молекул или ионов,

поэтомуэтоадстакуюцияэлектролитовадс-цию называют,приИАадсполярнойсяионы.адсВэтом-циейслучаенаадсциюсущественносказываетсяприродаадста..

На адсорбцию ионов влияет радиус ионов. При одинаковой валентности максимальную адсорбцию

m 7 10 ; оксиэтилированные алкилфенолы Сn H 2n 1 C6 H 4 O (CH 2 CH 2

O )m H ,

проявляет ион с большим радиусом

Радиус определяет гидратности оболочки и поляризованность, чем он больше тем выше полярность иона

n 12 18 , m 7 10; полиэтиленгликолевые эфиры жирных кислот

тем меньше его гидратная оболочка.

Ряды ионов напис в порядке уменьшения их связывать среду назыв-ся лиотропными рядами r

Сn H 2n 1COO( CH CH 2 O )m H . Оксиэтилированные спирты легко разлагаются в биосреде, а

увеличивается, R уменьшается литий меньше натрия меньше калия меньше цезия.

оксиэтилированные алкилфенолы – нет.

Обязательна одинаковая валентность

Фторированные ПАВ могут относиться к любому классу – быть ионными,

неионными,

или амфотерными. Их

Чем выше валентность тем больше адс-ционная способность.

особенность состоит в том, что при гидрофобной части молекулы, состоящей из 8 атомов углерода, они проявляют

38 КлассификацияПАВпохимическомустроению

свойства, характерные для углеводородных соединений с той же полярной группой, содержащих 16 ÷ 18 атомов

По химическим свойствам в соответствии с характером диссоциации полярных групп ПАВ делятся на

углерода. Фторированные ПАВ характеризуются высокой поверхностной активностью при низких концентрациях.

анионные, катионные, амфолитные и неионогенные

В мировом производстве ПАВ 60% составляют анионные, 30%-неионные, 10%-катионные, и лишь доли %

39 Коллоидные поверхностно-активныевещества.Мицеллообразование,строениемицеллвводнойи

- амфолитные. Анионные ПАВ - это органические соединения, молекулы которых, диссоциируя в воде,

образуют анион с крупным углеводородным радикалом, обладающий поверхностной активностью.

углеводороднойсреде.

Жирные кислоты и их соли, алкилсульфаты, алкилсульфонаты, алкиларилсульфанаты

тау мутность можно определить нефилометрически

( RCOO

, RArSO

ROSO

RSO

)

π давление пов-тной пленки

Катионные ПАВ диссоциируют в воде с образованием органического катиона, обладающего

n показатель преломления

поверхностной активностью. К ним относятся алифатические и ароматические амины, их соли четырех

замещенные аммониевые основания, производные пиридина. Катионные ПАВ содержат гидрофильные

μ (λ)

функциональные группы NH 3 ,

N (CH 3 )3

. С помощью катионных ПАВ стабилизируют дисперсные

Водные растворы ПАВ проявляют необычные физико-

системы с получением положительно заряженных частиц. Катионные ПАВ являются токсичными и

химические свойства. В разбавленных растворах ионные

ПАВ ведут себя как нормальные электролиты. При

наименее биоразлагаемыми из всех ПАВ.

достижении определенной концентрации резко

Амфолитные ПАВ содержат в молекуле кислотную (карбоксильную) и основную (амино) группы. В

изменяются такие физико-химические свойства, как

зависимости от

pH среды они проявляют свойства как катионных, так и анионных ПАВ и могут вести

осмотическое давление, электропроводность, мутность и

себя как неионогенные. К ним относятся аминокислоты и белки.

поверхностное натяжение

В водной среде образуются мицеллы ядро углевод

Неионогенные ПАВ содержат гидрофильные функциональные группы -ОН,

(CH 2 CH 2

O )H .

радикалы по пов-ти располагаются полярные группы -

прямая миц. Причиной образования мицелл в водной

Общая формула неиогенных ПАВ имеет следующий вид:

R x(CH 2 CH

2 0)m H

, где

среде явл-ся гидрофобное взаимодействие, т.е. взаимодействие гидрофобных молекул в полярной водной среде. Вода

C6 H 4 O ;

COO .

стремиться к вытеснению гидрофобных тел, т.к они нарушают ее структуру

x O ;

Мицелообразование в неполярных системах, ядро составляют полярные группы. Структура растворителя не

разрушается и энтропийный фактор не играет существенной роли, движущей силой явл-ся энтальпия, связано это с

выгодностью замены связи полрная группа-растворитель на связь полярная группа – полярная группа в ядре мицеллы.

При этом выделяется большое количество энергии, что очень выгадно, при малых колич молекулы ПАВ находятся в

состоянии предмицельных агрегатах.

40 Двемоделимицеллообразования

Tk - нижний предел температуры существования

41 Термодинамикаобразованияпрямыхиобратныхмицелл

СМ39

мицеллярных растворов, зависимость выше тчк Крафта наз-

+вводнойсредеПутисниженияэнергии: 1адсорбция(углеводныйрадикалуходитнапов-ть) 2) образованиемицелл(углеводный

радикалуходитизводывядромицелл) «2» самопроизвольныйпроцессследовательноуменьшаетизменениеэнергииГиббса,

ся линией Крафта.

энтальпиявпроцессемицеллобразованияизменяетсянезначительно,м.б.равно0, Энтропиясистемы= энтропияПАВ+энтропия

воды Sсист=SПАВ+ SВоды

энтропия ПАВ при образ мицелл уменьшается, а энтропия воды увеличивается.

42 Критическаяконцентрациямицеллообразования(ККМ). МетодыопределенияККМ. Влияние

различныхфакторовнавеличинуККМвполярныхинеполярныхсредах.

Абсцисса точки излома соответствует критической концентрации мицеллообразования (ККМ), т. е.

концентрации, выше которой становится возможным образование мицелл.

45 ВлияниетемпературынарастворимостьнеионогенныхПАВ.Точкапомутненияиточкавысаливания.

1Влияние длины углеводородного радикала : чем длиннее радикал тем более гидрофобна молекула тем

хуже растворение в воде тем ниже ККМ

2Влияние строения углеводородного радикала:

Величина ККМ при равном количестве атомов возрастает

Растворимость ПАВ уменьшается с повышением температуры, Для них характерна точка помутнения.

(по сравнению с парафиновой цепью): а) при включении циклов в цепь (алкилсульфонаты по сравнению с

Растворимость оксиэтилированных ПАВ в воде обусловлена образованием гидратов вследствие

алкилбензолсульфонатами); б) при введении в углеводородный радикал полярных групп, гетероатомов

возникновения водородных связей между молекулами воды и эфирными кислородными атомами

(олеат натрия по сравнению с рициноолеатом натрия). Наличие ароматических циклов, кратных связей,

полиэтиленгликолевого остатка. При нагревании эти связи ослабевают, происходит их

гетероатомов приводит к уменьшению гидрофобности углеводородного радикала и следовательно к

повышению ККМ

дегидратация, то есть уменьшение растворимости молекул ПАВ, что приводит к появлению

3 Влияние добавок электролитов : Величина ККМ при равном количестве атомов возрастает (по сравнению

опалесценции, а затем и к помутнению раствора. При дальнейшем нагревании этого раствора

с парафиновой цепью): а) при включении циклов в цепь (алкилсульфонаты по сравнению с

происходит укрупнение частиц вплоть до выделения капелек ПАВ в

виде отдельной фазы, то есть

алкилбензолсульфонатами); б) при введении в углеводородный радикал полярных групп, гетероатомов

их “высаливание”. Температура помутнения раствора (TП ) и температура высаливания раствора

(олеат натрия по сравнению с рициноолеатом натрия). Наличие ароматических циклов, кратных связей,

гетероатомов приводит к уменьшению гидрофобности углеводородного радикала и следовательно к

(TВ ) ПАВ часто используются в качестве характеристики степени полиоксиэтилирования

повышению ККМ

4 Влияние полярных органических веществ: длинноцепочечные спирты уменьшают ККМ,

промышленных продуктов и влияния различных добавок на их растворимость .

одновременно возрастает размер образующихся мицелл и вязкость раствора ПАВ, засчет образования

смешенных мицелл ПАВ+спирт. Ввод низкомолекулярных орг-х соединений уменьшает полярность среды,

увеличивает растворимость ПАВ следовательно увеличивает ККМ

43СолюбилизацияврастворахмицеллообразующихПАВ. Механизмысолюбилизациивмицеллах ПАВ.Влияниеразличныхфакторовнасолюбилизацию

Солюбилизацией называется захват ядром мицеллы третьего компонента мицеллярного раствора. Прямые мицеллы солюбилизируют углеводороды, обратные мицеллы – воду и полярные вещества. движущая сила

– положительное изменение энтропии.

1Увеличение олеофильности мицелл и усиление гидрофобных взаимодействий способствует солюбилизации.

2Солюбилизация увеличивается при уменьшении олеофильности солюбилизата

3уменьшается при введении циклов, двойных связей

44ВлияниетемпературынарастворимостьионогенныхПАВ.Диаграммасостояниясистемы.

ТочкаКрафта

Растворимость ионогенных ПАВ в воде вначале медленно, а затем быстро увеличивается с повышением температуры, их фазовое состояние определяется точкой Крафта

http://www.mitht.org/forum/

46 ПолиморфныепревращениямицеллколлоидныхПАВ.Лиотропныежидкиекристаллы.

48 Методыдиспергирования.УравнениеРебиндерадляработыизмельчения

лиотропные ЖК, которые представляют собой двух или более компонентные системы, образующиеся в

методы

основаны на

механических

способах преодоления

межмолекулярных сил.

Накопление

свободной

смесях стержневидных молекул данного вещества и воды (или других полярных растворителей). Эти

энергии

процессе

диспергирования происходит за счет

внешней механической

работы, переходящей в

стержневидные молекулы имеют на одном конце полярную группу, а большая часть стержня представляет

свободную

поверхностную энергию.

Диспергированием называют

измельчение твердых или жидких тел.

собой гибкую гидрофобную углеводородную цепь. Такие вещества называются амфифилами (амфи — по-

гречески означает с двух концов, филос — любящий, благорасположенный). Примером амфифилов могут

Диспергирование может происходить в результате процесса раздавливания, истирания, дробления.

служить фосфолипиды.Амфифильные молекулы, как правило, плохо растворяются в воде, склонны

При диспергировании можно установить взаимосвязи поверхностных и объемных свойств. Под действием

образовывать агрегаты таким образом, что их полярные группы на границе раздела фаз направлены к

жидкой фазе. При низких температурах смешивание жидкого амфифила с водой приводит к расслоению

внешних

сил

конденсированное вещество сначала претерпевает

объемное деформирование

(упругое и

системы на две фазы. Одним из вариантов амфифилов со сложной структурой может служить система

мыло-вода. Здесь имеется алифатический анион СН3-(СН2)n-2-СО2- (где n ~ 12-20) и положительный ион

пластическое)

и только

после этого

при

определенном

усилии

оно разрушается

с образованием новой

Nа+, К+, NН4+ и др. Полярная группа СО2- стремится к тесному контакту с молекулами воды, тогда как

поверхности. Таким образом, работу, необходимую для диспергирования, можно разделять на две части. Одна

неполярная группа (амфифильная цепь) избегает контакта с водой. Это явление типично для амфифилов.

часть работы расходуется на объемное деформирование тела:Wдеф

K V (7.2)

47 КоличественныехарактеристикисвойствПАВ.ЧислаГЛБ.РасчетчиселГЛБпометоду

,где К - коэффициент

Дэвиса

Одной из характеристик дифильных свойств коллоидных ПАВ является гидрофильно-липофильный баланс

пропорциональности,

равный

работе

объемного

деформирования

единицы

объема

(ГЛБ), характеризующий соотношение масс гидрофильной полярной группы и липофильного

конденсированного тела; V- объем тела.

углеводородного радикала. Число ГЛБ определяют путём сравнения способности различных ПАВ к

стабилизации эмульсий. Девис установил количественную связь ГЛБ от состава и структуры ПАВ. Каждая

структурная единица вносит свой вклад в числа ГЛБ.

Другая часть работы расходуется на образование новой поверхности:

Метод Девиса ГЛБПАВ 7 (ГЛБ) Г (ГЛБ)Л Число ГЛБ для данного

Wпов

s (7.3)

ПАВ можно рассчитать по аддитивной формуле, зная числа ГЛБ для каждой структурной единицы. При

низком значении числа ГЛБ (1÷4) ПАВ не растворяются и не диспергируются в воде. При значении числа

Полная работа, затрачиваемая на диспергирование, выражается уравнением Ребиндера:

ГЛБ от 8 до 10 они образуют в воде стабильные дисперсии типа молока, а выше 13 - образуют прозрачные

W W

K V s (7.4)

растворы.

пов

деф

В зависимости от числа ГЛБ изменяется функциональное назначение ПАВ, чем

определяются следующие их области применения: эмульгаторы в/м - 3÷6, смачиватели - 7÷9, эмульгаторы

м/в - 8÷13, моющие вещества - 13÷15.

Система ГЛБ облегчает рациональный выбор ПАВ для решения той или иной задачи:

подбора эмульгатора для образования прямой или обратной эмульсии, пенообразователя, солюбилизатора.

49 Адсорбционноепонижениепрочности(эффектРебиндера).Прочностькакповерхностное свойствоматериалов.

Ребиндер высказал предположение о том, что причиной понижения прочности твердых тел под влиянием поверхностно-активных веществ (ПАВ) лежит снижение свободной поверхностной энергии и, как следствие, уменьшение работы, необходимой для образования новых поверхностей, т.е. адсор ПАВ способствует разрушению.

Существует выражение: связанная прочночть реального ТВ тела имеющего диффект в виде микротрещен с пов-тной энергией

P0 ~ l E 1/ 2

Pид		E		E	где	b – размер молекул. Уравнение Гриффитса может быть также

	b		b

представлено в виде P0 ~ b Pид c

1при адс-ции в-в на пов-ти микротрещен, приводит к разрастанию микротрещен

2молекулы адс-ые на пов-ти микротрещен препятствуют силе сцепления на пов-ти микротрещен

ине могут самозалечиваться

3адсорбция молекул препятствует их регенирации (повторн слипанию) тем самым способ получению частиц с меньшим размером Адсорбция понижения прочности получило название Эффекта РЕБИНДЕРА.

50 Конденсационное образование лиофобных дисперсных систем. Термодинамические основы
гомогенного зародышеобразования (по Гиббсу–Фольмеру). Уравнение для работы образования
критическогозародыша.
Конденсация – процесс возникновения новой фазы в результате соединения молекул и ионов в
гомогенной среде конденсата сосотоит из двух параллельных процесса.
1Образование новой фазы
2 образование зародышей новой фазы в пересыщенном метастабильной системе
3 Рост зародышей приводят к образованию дисперсн частиц
Размеры образующихся частиц зависит от соотношения 2-х одновременно идущих процессов (их
скоростей) а= Vрост зарод/Vобразование зарод.
Термодинамика

51 Химическиеифизическиеметодысозданияметастабильностивсистеме.Зависимость				53 Принципыпостроениямицеллионностабилизованныхзолей.Привестипримеры.
размерачастицотразличныхфакторов				Мицелла - это отдельная частица дисперсной фазы коллоидной системы с жидкой дисперсионной средой,
физические такие как изменения давления, температуры, процесс конденсации пара, а так же				состоящая из кристаллического или аморфного ядра и поверхностного слоя, включающего сольватно
замена растворителя.				связанные молекулы окружающей жидкости.
Химические : Любая реакция, приводящая к образованию нерастворимого соединения или летучего					Рассмотрим		образование мицеллы на примере реакции хлорида	бария	с	сульфатом
соединения, а в случае конденсированных фаз и нелетучего - взаимодействии газов.				натрия Na2 SO4			BaCl2 BaSO4 2NaCl
По теореме Веймарна размеры образ частиц зависят от соотношения скорости образования зародышей.				натрия Na2 SO4			BaCl2 BaSO4 2NaCl
Если нужно получить систему с большой степенью дисперстности то скорость образования зародыша,
должна превышать скорость роста частиц.					Избыток одного из компонентов действует как стабилизатор коллоидного раствора. Пусть в избытке
Размер частиц зависит от конц реагентов: При низкой
Размер частиц зависит от конц реагентов: При низкой
конц исходн реагентов скорость образов зародыша				находится		BaCl2 . Вначале образуется агрегат мицеллы, являющийся				мельчайшим
высока, а скорость роста частиц мала				находится		BaCl2 . Вначале образуется агрегат мицеллы, являющийся				мельчайшим
В области 1 скорость нуклеации Vн				кристалликом.
достаточна, но Vк	скорость роста	кристаллов
невелика, так как	концентрация С	небольшая.				{mBaSO4 nBa2 2(n x)Cl }2xCl
Поэтому образуется коллоидная система - золь. В области 2 с увеличением концентрации V

			к			агрегат
			к				ядро
роста увеличивается, частицы быстро укрупняются и под действием силы тяжести оседают,
							частица
образуется осадок. В области 3 при высокой концентрации вещества, образующего дисперсную
							мицелла
фазу, вязкость возрастает, скорость диффузии вещества из раствора к поверхности зародыша				Х – наход неспосред близости от пов-ти и притягиваться за счет электростатических сил , эта часть ионов в тепловом
уменьшается. При высокой скорости нуклеации образуется много мелких частиц, которые				движении

соединяются друг с другом, образуя структированную коллоидную систему – гель.							Принципы построения формулы мицелл
52 Гетерогеннаяконденсация				1.	Агрегат мицеллы должен быть нерастворимым соединением.
Если в системе есть к-л поверхн, стенки сосудов, пылинки, которые могу избирательно смачиваться новой				1.	Агрегат мицеллы должен быть нерастворимым соединением.
фазой в присутствии старой, то в этом случае конденсация пройдет по гетерогенному механизму. Эти				2.	Потенциалопределяющими ионами могут быть ионы, образующие дисперсную, фазу, изоморфные
постороннии включения будут играть роль центров конденсации, при этом форма образующихся частиц				2.
						им ионы или органические ионы с высокой адсорбционной способностью.
будет зависеть от того , какая фаза новая или исходная лучше смачивает поверхнось
Работа образов критич зародыша по гетерогенному механизму Wобркр= f(ϴ)Wгомоген обр. кр.				3.	Противоионы образуют с потенциалопределяющими ионом растворимое соединение.
f(ϴ) – коэф-т описывающ как соотношение свободных пов-ной энергий образов зародыш по гетерогенному				3.
				4.	Мицелла в целом электронейтральна.
механизму так и отношение объемов зародыша				4.	Мицелла в целом электронейтральна.
f(ϴ) может изменяться от 0-1 при измен угла от 0 до 180 град. При угле 180 град f(ϴ)=1, тогда гетерогенная
работа равна гомогенной. Если угол равен 0, то f(ϴ)=0 и работа образования 0. если f(ϴ) от 0 до 1 работа
гетерогенного образов меньше чем работа гомогенного образов. Поскольку коэф-т будет меньше 1.

http://www.mitht.org/forum/

55 Получениелиофильныхколлоидныхсистемпутемсамопроизвольногодиспергирования. Выводуравнения

54 Пептизациякакфизикохимическийметодполученияколлоидныхсистем. Механизмы

Ребиндера-Щукина.

Многие коллоидные системы могут возникать спонтанно, или самопроизвольно. Эти системы называются

пептизации. Правило осадков ОствальдаПептизацией

называют расщепление

на первичные

лиофильными коллоидными системами, так как взаимодействие между веществом дисперсной фазы и средой

частицы под действием внешней среды агрегатов, возникающих в результате обратимой коагуляции

достаточно большое.

Изменение свободной энергии при самопроизвольном диспергировании может быть

дисперсных систем. Существуют три способа перевода осадка в коллоидный раствор. Адсорбционная

выражено следующим образом:

пептизация. В этом случае отталкивание частиц осадка друг от друга вызывается ДЭС,

F U S12

T S

(7.15)

образующимся на

поверхности частиц при

адсорбции

ионов добавляемого

электролита-

При

добавлении

объем системы

не меняется

U 0 .

Поверхность при

диспергировании

стабилизатора.Пептизация путем поверхностной диссоциации. Связана с образованием ДЭС

S 0 .

методом поверхностной модификации. Пептизатор здесь способствует процессу диссоциации с

увеличивается, т.е. s12

0 . Энтропия системы при дроблении также возрастает:

поверхности, вызывая образование растворимых соединений на поверхности частиц.Пептизация

Для самопроизвольного протекания процесса должно выполняться условие

F 0. Это условие

путем промывания осадка. Применяется в том случае, когда на поверхности частиц в осадке есть двойные

электрические слои, но они сжаты вследствие большой концентрации электролита. При промывании

будет выполнимо, если возрастание свободной энергии из-за увеличения поверхности при диспергировании

такого осадка водой концентрация электролита в нем уменьшается, двойные слои увеличивают свою

будет меньше убыли свободной энергии из-за возрастания энтропии:

толщину; силы электростатического отталкивания между частицами будут действовать на более далеких

S12

12 T S

(7.16)

расстояниях и вызовут коллоидное растворение осадка. При пептизации наблюдается характерная

Изменение поверхности пропорционально числу частиц n, умноженному на размер частиц в квадрате

зависимость между количествами пептизированного вещества,

S ~ na2 . Изменение энтропии T S ~ n K T ,

где

взятого осадка и пептизатора. Эту закономерность называют

т.е.

кинетической энергии частиц,

правилом осадка Оствальда. Она заключается в

том, что при

безмерный коэффициент, равный ~ 30.

постоянном содержании пептизатора с возрастанием количества

n a2

n k T (7.17)

взятого для пептизации осадка количество осадка, перешедшего в

раствор, сначала увеличивается, а затем уменьшается. Такую

Из этого уравнения можно получить критическое значения поверхностного натяжения:

зависимость можно объяснить тем, что для коллоидного диспергирования необходимо определенное

количество пептизатора. При малых количествах осадка его достаточно для образования адсорбционного

кр

(7.18)

слоя на каждой частице. С увеличением количества осадка, взятого для пептизации – пептизатор

распределяется по большому количеству частиц.

На каждой

частице его становится

все меньше и,

для частиц a 10 8 м,

2 .

наконец, его не достаточно для образования устойчивой системы, поэтому количество пептизированного

кр 0,01кДж м

осадка уменьшается, и пептизация может совсем не происходить.

Самопроизвольное диспергирование возможно для коллоидных систем, в которых

кр

Несмотря на большую межфазную поверхность в лиофильных дисперсных системах, малое межфазное

натяжение обуславливает сравнительно небольшую поверхностную энергию, которая способна

компенсироваться энтропийной составляющей. Малое значение 12 возможно только при значительном

межфазном взаимодействии, характерном для жидких сред.

56 Броуновскоедвижение,егопричиныиобщенаучноезначение

58 Понятие о диффузии. Первый и второй законы Фика. Физический смысл коэффициента диффузии, его

Природа броуновского движения состоит в том, что молекулы среды (жидкости или газа)

размерность.

сталкиваются с частицей дисперсной фазы,в результате чего она получает громадное число

Диффузией

называется самопроизвольный

процесс

переноса

вещества.

приводящий

ударов с разных сторон. Если частица имеет большие размеры, то число этих ударов так велико,

выравниванию концентраций и химического потенциала в результате теплового движения молекул,

что вследствие статистического закона импульсы взаимно компенсируются, и результирующий

импульс равен нулю. Если частица мала, то возрастает вероятность того, что число или

ионов и частиц. Диффузия является необратимым процессом, сопровождающимся ростом энтропии, так как

интенсивность ударов молекул с одной стороны будут больше, чем с другой. Результирующая

он переводит систему в наиболее неупорядоченное состояние. В однокомпонентной системе говорят о

сила вызовет смещение частицы. Движение частицы указывает на тепловое движение молекул

среды, так же, как качка корабля на море указывает на существование волн. В броуновском

самодиффузии вследствие теплового движения частиц или молекул. В многокомпонентных системах говорят

движении участвуют частицы с размером менее 5 10 6 м.

о взаимодиффузии, приводящей к выравниванию концентраций.

Теория броуновского движения сыграла громадную роль в науке. Теоретическое обоснование тепловой

перенос массы в соответствии с общей теорией потоков описывается уравнением

природы броуновского движения явилось доказательством реальности существования молекул,

отрицаемых Махом и Вильгельмом Отсвальдом. В связи с этим теория броуновского движения

dс

(8.2)

убедительно склонила чашу весов в пользу материалистического мировоззрения

dm D dx s d

57 Соотношениемеждусредне-квадратичнымсдвигомикоэффициентомдиффузии.Вывод

где dm - количество продиффундировавшего вещества,

D - коэффициент диффузии,

dc - градиент

уравненияЭйнштейна–Смолуховского через плоскость за время t будет перенесено

вещества. Если

концентрации, s - площадь, через которую идет диффузия,

- время. Знак «минус» перед правой

достаточно мало (или, что то же самое – мало время t), то

частью уравнения стоит потому, что с увеличением

x величина

c уменьшается, и производная dc

отрицательна. Первый закон Фика характеризует стационарный процесс диффузии. Стационарным

называется процесс, который зависит только от разности аргументов.

(8.3)

или

(2.2.88)

Когда градиент концентрации постоянен, можно записать: m D dс s

(знак минус ставится по тем же причинам, что и в уравнении Фика). Следовательно, очевидно, что

При

s 1 , 1,

m D , то

есть коэффициент

диффузии численно равен

количество вещества, перенесенного за 1 с, составит

. (2.2.89) Если площадь

количеству вещества, продиффундировавшего через единицу площади в единицу времени при градиенте

плоскости М равна 1, то уравнение (2.2.89) перейдет в уравнение для диффузионного

концентрации, равном единице.

потока

. (2.2.90) Сравнивая его с уравнением закона Фика, видим

Размерность коэффициента диффузии получается из выражения (8.3)

моль [D]

моль

см2 с

[D]

; [D] см2

см3 см

см2

. (2.2.91) Поэтому

, но

. (2.2.92)

Исходя из первого закона Фика, при s 1 и 1

iд

Cледовательно,

. (2.2.93) Из уравнения (2.2.93) видно, что

пропорционален t

1/2

Величина iд называется потоком диффузии.

Коэффициент диффузии для газов или веществ, слабо взаимодействующих со средой, в которой

происходит диффузия, не зависит от концентрации.

Тогда

, (2.2.94) поэтому

или

Второй закон Фика характеризует нестационарный процесс диффузии и описывает накопление

вещества в различных точках пространства в зависимости от времени поглощения вещества твердым телом,

то есть сорбцию: dс

d 2

с (8.4)

Зависимость коэффициента диффузии от температуры выражается уравнением типа уравнения

Аррениуса: D DOe ED RT

(8.5)

где ED - энергия активации диффузии.

http://www.mitht.org/forum/

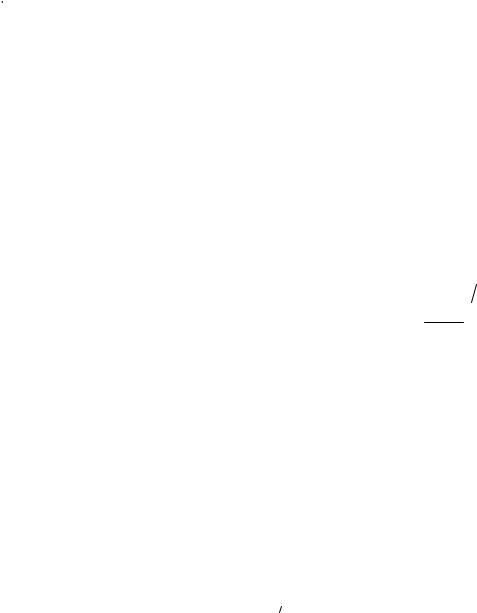
59 Диффузионно-седиментационноеравновесие.Выводгипсометрическогозакона.

ch до c0

и от нуля до h получим: ln c0

m g h ;

m g h

В соответствии с первым законом Фика поток диффузии iд D dс . Поток седиментации

После интегрирования от

e k T ;

iс U с, где U - скорость седиментации, c - концентрация.

k T

cO e

m g h

При равномерном оседании вес частицы

mg уравновешивается силой трения

k T (8.11)Это частный случай распределения молекул по Больцману. Если значение c заменить

пропорциональным ей значением p, получим:

mg ,

( mg BU ), где В - коэффициент трения. Отсюда:

iс

m g

.(8.10)

m g h

или

k T ln

g h

(8.12)

Если соотношение

, то системы грубо дисперсны, седиментационно неустойчивы,

k T

Это выражение известно под названием гипсометрического закона, определяющего распределение молекул газа по

iд

высоте. Согласно формуле (8.12), давление воздуха на высоте 6 км уменьшается вдвое. Левая часть уравнения (8.12)

диффузию для них можно не принимать во внимание. Если

iс

то системы обладают

представляет собой работу обратимого изотермического расширения моля газа от давления

до давления

ph .

iд

Правая часть уравнения является работой поднятия моля газа на высоту

h .

высокой

седиментационной

устойчивостью.

В расчет

можно

принимать

только диффузию,

60 Седиментациявгравитационномполе.Выводуравнениядляопределениярадиусачастицдисперснойфазы

iс

седиментация ничтожна. Такое положение характерно для истинных растворов. Если

то

поскоростиседиментации.УсловиясоблюдениязаконаСтокса.Седиментационноеуравнениенезаряженной

частицы

iд

Рассмотрим седиментацию незаряженной частицы, масса которой равна m, а объем -V, в жидкости

есть

iс

iд ,

то

следует

учитывать оба

процесса:

седиментацию

диффузию,

при

этом

плотностью

На частицу действуют направленные в разные стороны сила тяжести

m g и сила

устанавливается

равновесное распределение

частиц

дисперсной

фазы по высоте.

Такое

Архимеда m0 g ,

где m0

- масса жидкости в объеме частицы,

равная V . Седиментационная сила,

положение характерно для коллоидных систем и растворов высокомолекулярных соединений.

При условии равновесия iс

iд :

k T

которая не зависит от формы частицы, равна их разности:

(8.14) где V

m g

с D dс ;

;

fс m g V

g m 1 V

- удельный объем частицы.При оседании частицы действует сила трения, равная BU , где B - коэффициент

m g с

k T

dс ;

dс m g dx

трения, U- скорость седиментации.

k T

При стационарном режиме оседания седиментационная сила уравновешивается силой трения.

Так как градиент концентрации изменяется по высоте, то dx dh .

(8.15)

m 1 V

g B

По уравнению (8.15) можно определить массу частицы, но это требует знания коэффициента трения.

соблюдении ряда условий, которые не всегда соблюдаются в реальных системах 1. Частицы

В качестве величины, зависящей только от размера и плотности частиц, вводят отношение скорости

должны быть сферическими. Это условие обычно выполняется для разбавленных эмульсий и

оседания

частицы

к центробежному

ускорению,

то

есть

величину

S dx

x ,

которую

называют

частиц полимеров, полученных методом эмульсионной полимеризации. Частицы суспензий часто

отклоняются от сферической формы, поэтому для них определяется некоторый эффективный

радиус частицы той же массы, движущейся с той же скоростью. Такой радиус называют

константой седиментации. Тогда

;

(8.17)

эквивалентным или эффективным.2. Отсутствие взаимодействия между частицами. Расстояние

k T

S m 1

k T S

между частицами должно быть достаточно большим, чтобы падение одних частиц не сказывалось

на скорости других. Поэтому анализ следует проводить при невысоких концентрациях (1-2%).3.

D 1

Необходимо, чтобы сосуд, в котором происходит седиментация, был намного больше размеров

Скорость оседания частицы очень мала, а угловая скорость вращения ротора велика. Поэтому абсолютные

частиц. Это необходимо для того, чтобы можно было пренебречь влиянием стенок, так как вблизи

стенок скорость оседания не следует закону Стокса.4. Движущиеся частицы должны быть

значения

S столь малы, что для ее измерения ввели специальную единицу, называемую сведбергом, в

твердыми и гладкими. Это условие связано с возможностью изменения формы частиц в

результате возникновения в них микропотоков. Условие не выполняется при течении эмульсий.5.

честь шведского исследователя. Величина

S является характеристической константой частицы. Значение

Отсутствие проскальзывания между оседающей частицей и средой. Необходимо, чтобы

частица хорошо смачивалась жидкостью, так как в уравнение (2.2.17) входит h – вязкость именно

S определяют при разных концентрациях и экстраполируют к нулевой концентрации.

жидкости.6. Скорость оседания должна быть постоянной, иначе сила тяжести не уравновесится

силой трения.7. Скорость оседания должна быть небольшой, в противном случае возникает

63 Определениемассычастицметодомравновесногоультрацентрифугирования

турбулентный режим течения, и тогда нельзя будет использовать вязкость h, соответствующую

ламинарному режиму течения.

При равновесном ультрацентрифугировании используют ускорения порядка (10

10 ) g . При установлении

62 Седиментациявцентробежномполе.Определениемассычастицметодомскоростного

равновесия частицы располагаются в виде полосы, ширина которой определяется соотношением процессов

ультрацентрифугирования/В методе скоростного ультрацентрифугирования применяются центробежные

седиментации и диффузии

ускорения порядка 105 g . При центрифугировании частица, удаляясь от оси вращения, двигается со все

Количество

вещества,

переносимого

через

единицу

сечения

кюветы,

dс

равно

возрастающей скоростью. Поэтому величину U в седиментационном уравнении следует заменить на

. Обратный поток вещества вследствие диффузии равен

iд

. В

ic c m 1 V

dx , где

x - расстояние частицы от оси вращения,

t - время. Центробежное ускорение равно

условиях равновесия

2 x , где - угловая скорость вращения. Тогда седиментационное уравнение принимает

dс

;

k T

;

с m 1

d D

вид:

;

k T ; dx

k T

(8.16)

x m 1 V

dс ;

dс .

k T

с m 1

m 1 V

k T

Интегрируя от

x1 до

x2 и от

c1 до c2 , получим

x22 x12

c2 ;

m 1

k T ln

2 k T ln c2

1 V

где

c1 и c2 - равновесные концентрации на расстояниях x1 и

x2 от оси вращения.

Равновесное ультрацентрифугирование является абсолютным методом определения масс частиц и

макромолекул. Значения масс вычисляются лишь из разности концентраций на расстоянии

x1 и

x2 от

оси вращения

http://www.mitht.org/forum/

64 Термодинамическаяседиментационнаяустойчивостьифакторы,влияющиенанее.

67 Видырэлеевскогорассеяниясветаиегоусловия.Физическаясущностьрассеяниясвета.

Термодинамическая седиментационная устойчивость связна с

iс

iд

Рассеянием называется преобразование светого потока одного направления в световые потоки разных направлений.

различают два вида рэлеевского рассеяния: рассеяние мутными средами и молекулярное рассеяние света.

Мера – гипсометрическая высрта. Высата на кот концентрация частиц уменьшается в е раз

Релеевское рассеяние можно наблюдать невооруженным глазом; для наблюдения молекулярного рассеяния

Зависит от изменения температуры ТСУ ( не зависит от вязкости и увеличивается с повышением

применяют чувствительные фотометры. Для рэлеевского рассеяния выполняются два условия: длина волны

остается постоянной λ = const и поглощение отсутствует

темпер, т.к. усиливается тепловое движение

Физическая сущность

he= KбТ/mотнg = KT/v (ρ-ρ0)g

Световая волнапременная электромагнитное поле

Попадая на частицу , возникают осциллирующие диполи – источник вторичной волн, т.е. падающие и рассеянные

65 Кинетическаяседиментационнаяустойчивостьифакторы,влияющиенанее

волны разные. В оптически однородной среде диполи хаотично расположенных волн гасят друг друга во всех

направлениях кроме направления первичного пучка. В оптически неоднородной сред полного рассеяния не происходит.

S является характеристической константой частицы. Значение S определяют при

Рассеяние света коллоидными системами приводит к мутности, наблюдаемой в виде эффекта

Величина

Тиндаля. Мутность вещества определяется выражением:

разных концентрациях и экстраполируют к нулевой концентрации. Для экстраполяции строят

e-τ l

(9.1)

зависимость величины, обратной константе седиментации и называемой кинетической

седиментационной устойчивостью (КСУ). КСУ обеспечивается гидродинамическими факторами:

I0 и

In – интенсивность первичного и проходящего пучков, l– толщина образца,

– мутность.

вязкостью и плотностью среды, плотностью и размером частиц.

где

КСУ= 1/Scед=9η/2r2(ρ-ρ0)

68 Индикатрисырассеянияполяризованногоинеполяризованногосветабольшимиималымичастицами.

66 Явления,наблюдаемыепривзаимодействиивидимогосветасвеществом

Малыми частицами

. Радиус – вектор интенсивности

Частица помещена в начало координат, размер частицы

Если размер частицы много меньше длины волны света , то свет может проходить через

среду без изменений своего направления и интенсивности, то есть I I0 . Такое положение

рассеянного света, наблюдаемый под углом , обозначим как I n . Интенсивность рассеянного света

наблюдается в оптически однородной среде. Под оптической однородностью понимают

зависит от поляризуемости молекулы α.

одинаковое значение коэффициента преломления в разных точках среды. Существует только

Проекция зависимости интенсивности рассеянной волны от угла наблюдения на плоскость чертежа

одна оптически однородная среда – вакуум. Все остальные среды оптически неоднородны. В

синусоидальна, то есть имеет вид, изображенный на рис. 9.2 пунктирной линией. Эта векторная диаграмма, т.

оптически неоднородной среде часть света, проходящего через среду, поглощается. При этом

е. огибающая, радиус-вектора интенсивности рассеянного света,

может происходить селективное поглощение некоторых длин волн, тогда наблюдается окраска.

называется индикатриссой рассеяния.

Вследствие поглощения интенсивность проходящего пучка ослаблена по сравнению с первичным

пучком, то есть I I0

. В грубодисперсных системах, для которых выполняется условие

a , существует граница между двумя однородными средами и наблюдаются явления

Рис.

9.2.

Проекция

угловой

зависимости

интенсивности

преломления и отражения света. Для коллоидных систем большое значение имеет рассеяние

рассеянного света на плоскость чертежа (__ __ __)

и плоскость,

света по Рэлею.

перпендикулярную

к чертежу

_).

Сплошной

линией

изображена

индикатрисса

рассеяния

неполяризованного света малой частицей.

Проекция этой же зависимости на плоскость, перпендикулярную к чертежу, имеет вид окружности

Теория светорассеяния

усложняется,

когда

размер

частицы превышает

. Такие частицы

не могут

(штриховая линия). Проекции индикатриссы рассеяния поляризованного света на две взаимно

перпендикулярные плоскости можно представить как две компоненты, на которые можно

рассматриваться как точечные центры рассеяния. Волны, рассеянные разными участками такой частицы,

Такимразложитьобразомнеполяризованный, индикатрисса рассеяниясвет: вертикальнуюнеполяризованногои горизонтальнуюсвета малой. Неполяризованныйчастоты представляетсвет

интерферируют, что вызывает их ослабление (рис. 9.3). Внутричастичная ослабляющая интерференция

можно представить как наложение горизонтально и вертикально поляризованной составляющей.

собой эллипс, сжатый по малой оси (сплошная линия).Для поляризованного света справедливо

равна нулю в направлении первичного пучка,

то есть при

0 . При этом волны, рассеянные двумя

соотношение2

, установленное Рэлеем:

– угол наблюдения,

– расстояние от наблюдателя до

разными точками,

находятся в одной фазе.

В обратном направлении волны,

рассеянные двумя точками,

(9.2)

sin

находятся в различных фазах,

и поэтому возникает ослабляющая интерференция. Угловая зависимость

0 n

проекции вектора интенсивности света, рассеянного такой частицей, несимметрична (рис. 9.4).

частицы.

Интенсивность рассеянного света велика в направлении первичного пучка и мала в обратном направлении.

Для неполяризованного первичного пучка справедливо выражение:

I r 2

8 4 2

(9.3)

(1 cos

)

Величина I

r 2

называется приведенной интенсивностью рассеяния, или отношением Рэлея.

Рис. 9.3. Рассеяние света большими частицами.

Первый член выражения, стоящего в скобках, единица, соответствует вертикально

поляризованной

компоненте

рассеянного

света,

второй

член, cos2θ. соответствует

горизонтально поляризованной компоненте.

Вследствие того, что интенсивность рассеяния пропорциональна

1 , голубой свет ( = 450 нм)

Рис. 9.4. Угловая зависимость интенсивности, рассеяния большой

λ4

красного ( = 650 нм)

частицей.

рассеивается сильнее

69 УравнениеРэлея,условияегопримененияианализ

2 n0 2

2 .

Для сферических частиц, не проводящих электрического тока, малых по сравнению с длиной

волны, в разбавленном растворе справедливо соотношение, установленное Рэлеем:

n 2

2 n

(9.4)

Зависимость интенсивности рассеяния от разности показателей преломления среды и фазы приводит к тому,

что при n

образуются прозрачные, не рассеивающие свет системы, например эмульсия глицерина в

I p

четыреххлористом углеводороде. Это имеет большое значение для определения молекулярной массы

показатели преломления дисперсной фазы и дисперсионной среды, –

где

–

сополимеров,

состоящих

из

полимерных

отрезков

(блоков),

образованных разными

мономерами

(блоксополимеров). Подбирая растворитель, показатель преломления которого равен показателю

численная концентрация, λ– длина волны. Это выражение справедливо для частиц диаметром

преломления одного из блоков, делают его невидимым. Тогда легко определяется молекулярная масса

40÷70 нм, что для видимого света соответствует 0,1 . Проанализируем уравнение Рэлея:

другого блока. Этот метод называется методом невидимок.

70 Оптическиеметодыисследованиядисперсныхсистем.Нефелометрия.Схеманефелометра.

Так как

I p

f ( ) то в разбавленных растворах можно определить численную

Определениеразмераколлоидныхчастицметодомнефелометрии.

концентрацию коллоидных частиц.

Методом нефелометрии измеряют непосредственно интенсивность света, рассеянного под некоторым

углом к падающему лучу света. Методом турбодиметрии измеряют ослабление интенсивности света,

I p f (V 2 ) I0 k V 2 I0 .

проходящего через дисперсную систему.

При постоянной весовой концентрации уменьшим объем частицы в х раз. Тогда увеличится в

х раз.

V 2

I p

При смасс = const уменьшение объема частицы в х раз вызывает изменение интенсивности рассеянного света не в х2, а в х раз. При коагуляции коллоидных систем увеличение объема частиц вызывает увеличение интенсивности рассеянного света.

3.I p f 14 .

Поэтому в случае видимого света синие лучи лучше рассеиваются, красные лучше проходят.

http://www.mitht.org/forum/

1 / 21 2 > Следующая >>>

Соседние файлы в предмете Коллоидная химия

#
24.03.20154.83 Mб139683.pdf
#
24.03.20151.93 Mб47684.pdf
#
24.03.20157.63 Mб64colloid_grig.pdf
#
24.03.20158.2 Mб135colloid_shpora.pdf
#
24.03.20154.8 Mб286kolda vse otvety.pdf
#
24.03.20151.41 Mб101kolda.pdf
#
24.03.2015937.09 Кб59kolda.pdf
#
24.03.2015291.05 Кб95kolda_test1.pdf
#
24.03.2015296.17 Кб74kolda_test2.pdf
#
24.03.2015331.93 Кб77kolda_test3.pdf
#
24.03.2015403.31 Кб99kolda_test4.pdf