
Семенов. Планирование эксперимента2
.pdfФедеральное агентство по образованию
Московская Государственная академия тонкой химической технологии им. М.В.Ломоносова
Кафедра Химии и технологии редких и рассеянных элементов им. проф. К.А.Большакова
С.А.СЕМЕНОВ
ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА В ХИМИИ И ХИМИЧЕСКОЙ ТЕХНОЛОГИИ
(часть 2)
Учебное пособие
Москва, 2005 г.
www.mitht.ru/e-library
ББК 24:30.606:В6 УДК 66-9.001.4/.5:65.012.2
Рецензент: проф. Закгейм А.Ю. (МИТХТ, кафедра общей химической технологии)
Семенов С.А.
Планирование эксперимента в химии и химической технологии (часть 2).
Учебное пособие.
М.: МИТХТ им. М.В.Ломоносова, 2005 - 29 с.: ил.
Утверждено Библиотечно-издательской комиссией МИТХТ им. М.В.Ломоносова в качестве учебного пособия.
Настоящее учебное пособие является продолжением пособия, опубликованного в 2001 г. Изложены методы оптимального планирования эксперимента в химии и хими-
ческой технологии. Методы иллюстрируются примерами расчетов. Учебное пособие ре-
комендовано для студентов 5-го курса, обучающихся по дисциплине «Планирование эксперимента» для направления 551600 и студентов 5-го курса, обучающихся по спе-
циальности 072200 «Метрология, стандартизация и сертификация (по отраслям)»
дневной формы обучения.
МИТХТ им. М.В.Ломоносова, 2005
2
www.mitht.ru/e-library
Оглавление
Условные обозначения и сокращения …………….……………….3
Введение …………………………………………………..…………….4
1.Функция желательности ……………………………………..…4
2.Сложные планы ……………………………………………...…14
Латинские и греко-латинские квадраты ……………………....14
Факторный эксперимент 22k, совмещенный с
латинским квадратом ……………………………….……………18
3. Ортогональные насыщенные планы Плакетта-Бермана ..23
Литература …………………………………………………………….27
Условные обозначения и сокращения
ПФЭ – полный факторный эксперимент.
ДФЭ – дробный факторный эксперимент. bi – коэффициент уравнения регрессии. D – обобщенная функция желательности. d – частная функция желательности.
k – количество факторов. l – число уровней.
N – количество опытов.
sвоспр. – дисперсия воспроизводимости. t – критерий Стьюдента.
xi – фактор.
yj – функция отклика.
3
www.mitht.ru/e-library
Введение
Настоящее учебное пособие является продолжением пособия, опуб-
ликованного в 2001 г. [1]. Ранее [1] были рассмотрены общие сведения об эксперименте, экспериментально-статистические модели, в том числе пол-
ный факторный эксперимент (ПФЭ), метод дробных реплик, устранение влияния временного дрейфа, дана интерпретация полученной модели;
рассмотрены методы оптимизации, в том числе метод крутого восхожде-
ния и симплексный метод, рассмотрено исследование области оптималь-
ных условий на примере ортогонального центрального композиционного планирования, рассмотрено планирование эксперимента при изучении диаграмм составсвойство, в том числе метод симплексных решеток, сим-
плекс-решетчатые планы Шеффе.
1. Функция желательности
Задачу оптимизации процессов, характеризующихся несколькими от-
кликами, обычно сводят к задаче оптимизации по одному критерию с огра-
ничениями в виде равенств или неравенств. В зависимости от вида по-
верхности отклика и характера ограничений, для оптимизации предлагает-
ся использовать методы неопределенных множителей Лагранжа, линейно-
го и нелинейного программирования, ридж-анализ [2, 3] и др. К недостат-
кам этих способов решения задачи оптимизации следует отнести вычисли-
тельные трудности. В частности, при описании поверхности отклика поли-
номами второго порядка решение задачи на условный экстремум с приме-
нением неопределенных множителей Лагранжа приводит к необходимости решать систему нелинейных уравнений. Поэтому одним из наиболее удач-
ных способов решения задачи оптимизации процессов с большим количе-
ством откликов является использование предложенной Харрингтоном [4] в
качестве обобщенного критерия оптимизации так называемой обобщенной
4
www.mitht.ru/e-library
функции желательности D. Для построения обобщенной функции жела-
тельности D предлагается преобразовать измеренные значения откликов в безразмерную шкалу желательности d. Построение шкалы желательности,
которая устанавливает соотношение между значением y и соответствую-
щим ему значением d (частной функции желательности), является в своей основе субъективным, отражающим отношение исследователя (потреби-
теля) к отдельным откликам.
Для построения шкалы желательности удобно использовать метод ко-
личественных оценок с интервалом значений желательности от нуля до единицы, хотя возможны и другие варианты шкалы. Значение d=0 (или
D=0) соответствует абсолютно неприемлемому значению данного отклика,
а d=1 (D=1) - самому лучшему значению отклика, причем дальнейшее улучшение его или невозможно, или не представляет интереса. Промежу-
точные значения желательности и соответствующие им числовые отметки приведены в табл. 1.
Таблица 1.
Базовые отметки шкалы желательности
Количественная отметка |
Желательность значения |
|
на шкале желательности |
отклика |
|
|
|
|
0.8 1.00 |
Очень хорошо |
|
|
|
|
|
0.80 |
Хорошо |
0.63 |
|
|
|
0.63 |
Удовлетворительно |
0.37 |
|
|
|
0.37 |
Плохо |
0.20 |
|
|
|
0.20 |
Очень плохо |
0.00 |
|
|
Такой выбор числовых отметок объясняется удобством вычислений, по-
скольку
5
www.mitht.ru/e-library

d 0.63 1 |
1 |
; |
d 0.37 |
1 |
(1.1) |
|
e |
e |
|||||
|
|
|
|
Построенная в соответствии с табл. 1 шкала d представляет собой без-
размерную шкалу, при помощи которой любой отклик может быть преобра-
зован так, чтобы его можно было интерпретировать в терминах полезности или желательности для любого специфического применения.
Простейшим типом преобразования служит такое, в котором сущест-
вует верхний и (или) нижний пределы, причем эти пределы являются единственным и не допускающим изменений критерием качества. Вне этих пределов значение d=0.0, между ними значение d=1. Частная функция же-
лательности при одностороннем ограничении имеет вид (рис.1,а). 0, y<ymin
d= |
(1.2) |
1, y ymin
Аналогичным образом получается частная функция желательности, ес-
ли задается ограничение сверху. Если для данного свойства существует двустороннее ограничение, то частная функция желательности будет вы-
глядеть следующим образом (рис.1,б).
0, y<ymin и y>ymax
d= |
(1.3) |
1, ymin y ymax
Всегда желательно, чтобы значение отклика находилось не только меж-
ду заданными пределами, но и на определенном расстоянии от них, чтобы противостоять присущим производственному процессу случайным колеба-
ниям. Кроме того, довольно трудно бывает провести точную пограничную линию между приемлемой и неприемлемой продукцией. Поэтому в общем случае преобразование y в d осуществляется по более сложным законам.
6
www.mitht.ru/e-library
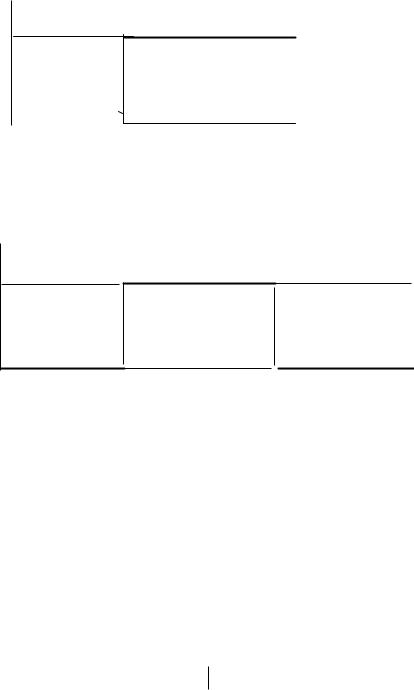
d 1
0
d 1
0
*
|
* |
y |
ymin |
||
|
a |
|
**
ymin |
ymax |
y |
б
Рис.1. Простейший случай задания частной функции
желательности
Для двустороннего ограничения вида
ymin y ymax
преобразование измеренного отклика y в шкалу d (рис.2) производится при помощи выражения
d exp[ ( |
y')n ], |
(1.4) |
где n - положительное число (0<n< ) не обязательно целое;
y' |
2y (ymax ymin ) |
; |
(1.5) |
|
|||
|
ymax ymin |
|
|
7
www.mitht.ru/e-library

показатель степени n можно вычислить, если
задать некоторому значению y значение d
(предпочтительно в интервале 0.6<d<0.9) по формуле
n |
ln(ln1/d) |
, |
(1.6) |
||
|
|||||
|
ln |
y' |
|
|
|
Задавая при помощи контрольной точки крутизну кривой желательности, можно учесть особую важность отдельных свойств; для них n будет иметь большее значение, и малому изменению свойства вблизи ограничивающих
пределов будет соответствовать резкое изменение желательности. Пока-
затель степени n определяет наклон кривой, и когда n становится боль-
шим, кривая приближается к своей предельной форме (см. рис.1,б): d=0
вне заданных пределов и d=1 между этими пределами. Если нет заданных пределов, целесообразно дать статистическую оценку n по ряду значений
y и соответствующих d. |
|
|
Для односторонних ограничений вида y ymax |
или y ymin более удобной |
|
формой преобразования y в d служит другая экс- |
||
поненциальная зависимость (рис.3): |
|
|
d=exp[-exp(-y')], |
(1.7) |
|
В выражении (1.7) |
|
|
|
y'=b0+b1y |
(1.8) |
Коэффициенты b0 и b1 |
можно определить, если |
|
Рис. 3. Функция желательности для свойства, ограниченного с одной стороны.
8
www.mitht.ru/e-library

задать для двух значений свойства y соответствующие значения жела-
тельности d предпочтительно в интервале 0.2<d<0.8.
Нелинейное преобразование y в y' применяется, если данное свойство имеет особую важность, нарушение условий недопустимо и малому изме-
нению свойства вблизи ограничивающего предела соответствует резкое изменение желательности. Односторонняя спецификация наиболее часто встречается на практике.
Имея несколько откликов, преобразованных в шкалу d, можно при по-
мощи арифметических операций скомбинировать из этих различных d не-
кий обобщенный показатель желательности D. При этом, если какой-либо один отклик является абсолютно неудовлетворительным, обобщенная функция желательности D должна быть равна 0 независимо от уровня ос-
тальных откликов. Математическим выражением, отвечающим этим требо-
ваниям, служит среднее геометрическое частных функций желательности,
т.е.
(1.9)
Очевидно, что если какое-либо одно di=0, то соответствующее D=0. Бо-
лее того, на D сильно влияют именно наименьшие значения di. В то же время D=1 только тогда, когда все частные желательности di=1 (i=1, 2, …, k). Важно еще то, что (1.9) позволяет применить к частным желательно-
стям и обобщенному показателю единый способ задания базовых отметок шкалы желательности, представленный в табл.1, так как если d1=d2=…=dk=0.37, то и D=0.37 и т.д. С обобщенной функцией желательно-
сти D можно проделывать все вычислительные операции, как и с любым откликом системы, можно использовать D в роли критерия оптимизации при исследовании и оптимизации процесса. Следует иметь в виду, что множество возможных значений D ограничено: 0 D 1.
9
www.mitht.ru/e-library

Пример 1.1. Функция желательности была применена при разработке композиции нового полимерного материала на основе полиэтилена высо-
кого давления. В качестве откликов были использованы: y1 - модуль упру-
гости при изгибе, кгс/см2; y2 - разрушающее напряжение при разрыве,
кгс/см2; y3 - относительное удлинение при разрыве, %, и D - обобщенная функция желательности. Покажем последовательность расчетов при опре-
делении D.
Для сравнительной оценки качества различных композиций обобщенную функцию желательности определяли по формуле
D 3 |
d1 d2 d3 , |
(1.10) |
где d1, d2 и d3 - частные функции желательности.
Для построения частных функций желательности необходимо сначала установить преобразование измеренных свойств y в безразмерную равно-
мерную шкалу y'. Ограничения при этом носят характер y ymin. Разрабаты-
ваемый материал должен удовлетворять заданным требованиям по трем показателям качества, которые предусматривают пригодность его к пере-
работке и эксплуатации. Исходя из этих требований, были выбраны значе-
ния y1, y2 и y3, соответствующие двум базовым отметкам на шкале жела-
тельности (табл.1). Преобразование отклика y в частную функцию жела-
тельности имеет вид (1.7). Коэффициенты b0 и b1 определялись по данным таблицы 2.
Подставим значение d в уравнение (1.7): 0.63=exp[-exp(-y'1)] и 0.2=exp[-exp(-y'1)],
1/0.63=1.587=exp[exp(-y'1)] и 1/0.2=5=exp[exp(-y'1)]. (1.11)
Дважды логарифмируя выражения (1.11), получим
-y'1=ln(ln1.587) и -y'1=ln(ln5)
или
-y'1=-0.755 и -y'1=0.326. |
(1.12) |
10 |
|
www.mitht.ru/e-library
