Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный университет тонких химических технологий им. М.В. Ломоносова

Предмет:

Высшая математика

Файл:

268.pdf

Скачиваний:

Добавлен:

24.03.2015

Размер:

468.6 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 117 8 9 10 11 > Следующая >>>

8.Изображение периодических оригиналов

Пусть f (t) — периодический оригинал с периодом T , т.е.
				f (t + T ) = f (t)
для всех t > 0 . Докажем теорему.
	Теорема. Изображение периодического оригинала f (t)						с пе-
		определяется формулой
риодом T		определяется формулой
				(p) =	ψ(p)		(91)
			f		ψ(p)	,
			f		1 −e−pT	,
где					1 −e−pT
где
				T
		ψ(p) = Z			f (t)e−pt dt.		(92)

Доказательство Разобьем промежуток интегрирования [0,∞) на два промежутка и, положив во втором из следующих ниже интегралов t = τ + T , получим ([0,∞) = [0,T ] [T,∞))

	∞		T	∞
	(p) = Z	f (t)e−pt dt = Z		f (t)e−pt dt + Z	f (t)e−pt dt =
f	(p) = Z	f (t)e−pt dt = Z		f (t)e−pt dt + Z	f (t)e−pt dt =
0		∞	0	T	∞
		∞			∞
= ψ(p) + Z			f (τ + T )e−p(τ+T )dτ = ψ(p) + e−pT Z			f (τ)e−pτdτ =
		0			0

= ψ(p) + e−pT f (p). (93)

Отсюда получаем

f (p) = ψ(p) + e−pT f (p)

www.mitht.ru/e-library

ψ(p)

f (p) = 1 −e−pT ,

что и требовалось доказать.

Функция ψ(p) , определяемая формулой (92), является изображением оригинала

( ) =	(	0,	t < 0,t > T.	(94)
ψ t		f (t),	0 ≤ t ≤ T

Можно доказать и обратную теорему: оригинал f (t) , изображение которого имеет вид (91), является периодической функцией с периодом T , которая получается при периодическом продолжении функции ψ(t) с отрезка [0,T ] на всю положительную часть оси t .

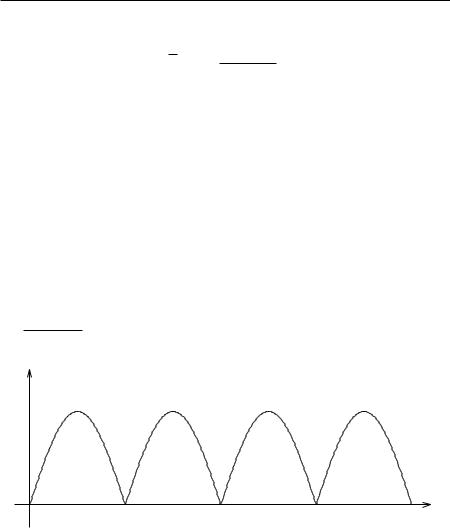
Пример. Найти изображение периодического оригинала, имеющего вид f (t) = A |sin wt| (рис. 8).

0	π/w	2π/w	3π/w	t
				4π/w

Рис. 8.

Функция f (t) имеет период T = wπ . Дважды интегрируя по частям, находим

www.mitht.ru/e-library

					45
T	π/w
ψ(p) = Z	f (t)e−pt dt = A Z	e−pt sin wtdt =
0	0	= p2 + w2		1 + exp	−w .
			Aw		T

Здесь было использовано изображение функции sin wt (см. ф. 5 табл. 2). Следовательно,

Aw 1

+ e− pTw

f (p) =

cth

(95)

p2 + w2

−e− pTw

p2 + w2

www.mitht.ru/e-library

9.Нахождение изображений функций непосредственно с помощью определения и с использованием таблиц изображений

Заметим предварительно, что в таблице и в каждом из приведенных ниже примеров указывается только значение f (t) при t > 0 (всегда имеется ввиду, что f (t) = 0 , если t < 0 ).

Найти изображение следующих функций, пользуясь определением (1):

9.1.f (t) = 1 .

9.2f (t) = t .

9.3f (t) = e−kt .

Решение.

9.1.

(

) =

∞

−

= − p

−

= − p N→∞

−

pt dt

1 e

∞

lim e

lim

e−

lim e−

= 0

(так как

, Re p > 0 )

−

N→∞

−

N→∞

9.2.

Находим изображение f (t) интегрированием по частям:

u = t

du = dt

dv = e−pt dt

e−pt

v = −

	∞	∞		∞
	(p) = 0 e−pt t = −1p te−pt	0	+	1p 0 e−pt dt =
f	(p) = 0 e−pt t = −1p te−pt	0	+	1p 0 e−pt dt =
	R			R
	∞		∞

9.3.f (p) = R e−kt e−pt dt = R e−(p+k)t dt =

p12 . (см. пример 1)

1 . (k 6=−p)

p+k

www.mitht.ru/e-library

											47
Итак, получено, что:
9.1.	.	1	(1		1						(см. табл. 2, ф.1)
9.1.	1 →.	p	(1		+ p );						(см. табл. 2, ф.1)
	.	1			1
9.2.	t →.			(t	+		);				(см. табл. 2, ф.3, n = 1 )
9.2.	t →.	p2		(t	+	p2	);				(см. табл. 2, ф.3, n = 1 )
9.3.	e−kt	..		1	(e−kt				1	).	(см. табл. 2, ф.4, α = k )
9.3.	e−kt	..			(e−kt			+ p+k		).	(см. табл. 2, ф.4, α = k )
		→ p+k						+ p+k			−

Найти изображение следующих функций, пользуясь табл. 2 и свойствами изображений.

9.4.f (t) = at .

9.5.f (t) = cos3(t) .

9.6.f (t) = sh bt .

9.7.f (t) = sh at sin bt .

9.8.f (t) = t ch bt .

Решение.

9.4. Представим функцию f (t) = at в виде f (t) = et ln a и применим формулу (4) в табл. 2 изображений, приняв α = ln a , получим

e−t ln a →.

, т.е. at +

−

ln a

−

ln a

9.5. По формуле Эйлера cost = eit +e−it , тогда

cos3 t =

2 −

e3it

+ 3eit + 3e−it + e−3it

eit + e

3it

+ e−

cos 3t +

cost.

www.mitht.ru/e-library

Пользуясь свойством 1 линейности изображений и формулой 6 табл. 2, а именно cos wt + p2p+1 , получим

cos3 t +	1	p	+	3	p	.
	4 p2 + 9
			4 p2 + 1

Впервом случае w = 3 , во втором — w = 1 .

9.6.По определению гиперболического синуса имеем

f (t) = 1 ebt − 1 e−bt .

2 2

Так как по табл. 2 ф. 4 ebt + p−1 b , e−bt + p+1 b и по свойству 1 линейности изображения получим

т.е. sh bt +

f (p) =

−

2(p −b)

2(p + b)

p2 −b2

(см. ф. 7 табл. 2)

9.7. Так как sh at = 21 (eat −e−at ) , то

f (t) = sh at sin bt =

eat sin bt −

e−at sin bt.

Применим ф. 12 табл. 2 (w = b , λ = a в первом слагаемом,

λ = −a во втором слагаемом)

eλt sin wt +

;

(p −λ)2 + w2

получим

www.mitht.ru/e-library

f (p) =

−

(p −a)2 + b2

(p + a)2 + b2

2pab

(p −a)2

+ b2

(p + a)2

+ b2

9.8. Пользуясь определением гиперболического косинуса,

можно записать

f (t) = t

ebt + e−bt

tebt +

te−bt .

Применяя ф. 9 табл. 2 (teαt +

) , приняв n = 1 , α = b в

(p−α)

первом слагаемом и α = −b во втором слагаемом), получим

p2 + b2

f (p) =

2(p −b)2

2(p + b)2

(p2 −b2)2

Найти изображения следующих функций:

9.9.f (t) = sin2 t.

9.10.f (t) = et cos2 t.

9.11.f (t) = ch bt.

9.12.f (t) = sh at cos bt.

9.13.f (t) = ch at sin bt.

9.14.f (t) = ch at cos bt.

9.15.f (t) = t sh bt.

Ответы:
		2
9.9.	f (p) =			.
		p(p2	+ 4)

www.mitht.ru/e-library


		p(p2	+ 2p + 3)
9.10.	f (p) =	p(p2	+ 2p + 3)		.
9.10.	f (p) =	(p −1)(p2		−2p + 5)	.
		(p −1)(p2		−2p + 5)

9.11.f (p) =

9.12.f (p) =

9.13.f (p) =

9.14.f (p) =

9.15.f (p) =

p . p2 −b2

a(p2 −a2 −b2)

p (p −a)2 + b2 (p + a)2 + b2

		b(p2a2 −b2)		+ b2	.
(p −a)2 + b2 (p + a)2				+ b2
	p(p2 −a2 + b2)			+ b2	.
(p −a)2 + b2 (p + a)2				+ b2
2pb			.
2	2	2	.
(p	−b	)

www.mitht.ru/e-library

<<< < Предыдущая 1 2 3 4 5 67 / 117 8 9 10 11 > Следующая >>>

Соседние файлы в предмете Высшая математика

#
24.03.2015468.6 Кб69268.pdf
#
24.03.20151.7 Mб19BANK2009дтф.DOC
#
24.03.20151.28 Mб13groups_lections (Множества и группы).pdf
#
24.03.20151.45 Mб60Teoria_ryadov_12.doc
#
24.03.2015778.09 Кб32Банк задач.pdf
#
24.03.2015410.49 Кб43Ожерелкова,Рубин,Джемесюк.Ряды.pdf