
- •21.Термодинамические параметры. Равновесные состояния и процессы. Внутренняя энергия идеального газа. Работа газа при изменении его объема. Количество теплоты. Первый закон термодинамики.
- •Частные случаи первого закона термодинамики для изопроцессов
- •22.Теплоемкость.Теплоемкость идеального газа при постоянном давлении и при постоянном объеме. Уравнение Майера
- •23.Применеие первого закона термодинамики при изохорическом, изобарическом, изотермическом процессах. Адиабатический процесс. Уравнение Пуассона. Работа идеального газа при адиабатическом процессе.
- •24.Второй закон термодинамики. Энтропия. Закон возрастания энтропии. Теорема Нернста. Энтропия идеального газа.
- •Энтропия идеальных газов
- •25. Цикл Карно и его кпд для идеального газа.
- •26. Барометрическая формула. Распределение Больцмана.
- •27. Закон Максвелла распределения молекул по абсолютным значениям скоростей. Средняя, средняя квадратичная и наиболее вероятная скорость молекул.
- •28. Столкновение молекул. Эффективное сечение молекулы. Число столкновений молекулы в единицу времени. Длина свободного пробега молекулы.
- •29.Диффузия в газах. Вязкость газов. Теплопроводность газов. Коэффициенты диффузии, вязкости, теплопроводности. Вывод формулы для коэффициента диффузии.
28. Столкновение молекул. Эффективное сечение молекулы. Число столкновений молекулы в единицу времени. Длина свободного пробега молекулы.
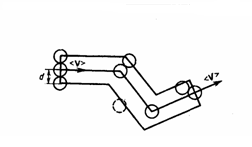
Молекулы газа, находясь в хаотическом движения, непрерывно сталкиваются друг с другом. Между двумя последовательными столкновениями молекулы проходят некоторый путь l, называемым длиной свободного пробега. В общем случае длина пути между последовательными столкновениями различна, но так как мы имеем дело с очень большим числом молекул и они находятся в беспорядочном движении, то можно говорить о средней длине свободного пробега молекул <l>. Минимальное расстояние, на которое сближаются при столкновении центры двух молекул, называется эффективным диаметром молекулы d (рис. 1). Он зависит от скорости сталкивающихся молекул, т. е. от температуры газа (несколько уменьшается с ростом температуры).

Рис.1
Так
как за 1 с молекула в среднем проходит
путь, который равен средней арифметической
скорости <v>, и если < z > — среднее
число столкновений, которые одна молекула
газа делает за 1 с, то средняя длина
свободного пробега будет
![]() Для
определения < z > представим себе
молекулу в виде шарика диаметром d,
которая движется среди других как бы
застывших молекул. Эта молекула столкнется
только с теми молекулами, центры которых
находятся на расстояниях, равных или
меньших d, т. е. лежат внутри так называемого
ломаного цилиндра радиусом d (рис.
2).
Среднее
число столкновений за 1 с равно числу
молекул в объеме, так называемого
ломаного цилиндра:
Для
определения < z > представим себе
молекулу в виде шарика диаметром d,
которая движется среди других как бы
застывших молекул. Эта молекула столкнется
только с теми молекулами, центры которых
находятся на расстояниях, равных или
меньших d, т. е. лежат внутри так называемого
ломаного цилиндра радиусом d (рис.
2).
Среднее
число столкновений за 1 с равно числу
молекул в объеме, так называемого
ломаного цилиндра:
![]() где
n — концентрация молекул, V = πd2<v>
,где <v> — средняя скорость молекулы
или путь, пройденным ею за 1 с). Таким
образом,среднее
число столкновений
где
n — концентрация молекул, V = πd2<v>
,где <v> — средняя скорость молекулы
или путь, пройденным ею за 1 с). Таким
образом,среднее
число столкновений
![]() Расчеты
показывают, что при учете движения
других молекул
Расчеты
показывают, что при учете движения
других молекул
![]() Тогда
средняя длина свободного пробега
Тогда
средняя длина свободного пробега
![]() т.
е. <l>
обратно пропорциональна концентрации
n молекул. С другой стороны, p=nkt.
Значит,
т.
е. <l>
обратно пропорциональна концентрации
n молекул. С другой стороны, p=nkt.
Значит,
![]()
29.Диффузия в газах. Вязкость газов. Теплопроводность газов. Коэффициенты диффузии, вязкости, теплопроводности. Вывод формулы для коэффициента диффузии.
Диффузия от латинского diffusio – распространение, растекание - взаимное проникновение соприкасающихся веществ друг в друга, вследствие теплового движения частиц вещества. Диффузия происходит в направлении уменьшения концентрации вещества и ведет к его равномерному распределению по занимаемому объему. Диффузия имеет место в газах, жидкостях и твердых телах. Наиболее быстро диффузия происходит в газах, медленнее в жидкостях, еще медленнее в твердых телах, что обусловлено характером движения частиц в этих средах.
Для газа диффузия – это распределение молекул примеси от источника (или взаимная диффузия газа).
Вязкость
газов (явление внутреннего трения) —
это появление сил трения между слоями
газа, движущимися друг относительно
друга параллельно и с разными по величине
скоростями.
Взаимодействие двух слоев
газа рассматривается как процесс, в
ходе которого от одного слоя к другому
передается импульс.
Сила трения на
единицу площади между двумя слоями
газа, равная импульсу, передаваемому
за секунду от слоя к слою через единицу
площади, определяется законом
Ньютона:
![]()
![]() —
градиент скорости в направлении
перпендикулярном направлению движения
слоев газа.
Знак минус указывает, что
импульс переносится в направлении
убывания скорости.
—
градиент скорости в направлении
перпендикулярном направлению движения
слоев газа.
Знак минус указывает, что
импульс переносится в направлении
убывания скорости.![]() —
динамическая вязкость.
—
динамическая вязкость.![]() ,
где
,
где![]() —
плотность газа,
—
плотность газа,![]() —
средняя арифметическая скорость
молекул,
—
средняя арифметическая скорость
молекул,![]() —
средняя длина свободного пробега
молекул.
—
средняя длина свободного пробега
молекул.
![]() —
кинематический
коэффициент вязкости.
—
кинематический
коэффициент вязкости.
ТЕПЛОПРОВОДНОСТЬ ГАЗОВ
Теплопроводность
газов — явление направленного переноса
тепловой энергии за счет столкновения
частиц газа без переноса вещества.
Явление
теплопроводности описывается законом
Фурье:
![]() ,
где
,
где
![]() —
плотность теплового потока, равная
тепловой энергии, переносимой за единицу
времени через единичную площадку,
перпендикулярную оси x.
—
плотность теплового потока, равная
тепловой энергии, переносимой за единицу
времени через единичную площадку,
перпендикулярную оси x.
![]() —
градиент температуры,
—
градиент температуры,![]() —
коэффициент теплопроводности.
—
коэффициент теплопроводности.![]() ,
где
,
где![]() —
средняя арифметическая скорость
молекул,
—
средняя арифметическая скорость
молекул,![]() —
средняя длина свободного пробега
молекул.
—
средняя длина свободного пробега
молекул.![]() —
число степеней свободы молекул газа,
—
число степеней свободы молекул газа,![]() —
постоянная Больцмана,
—
постоянная Больцмана,![]() —
концентрация частиц газа,
—
концентрация частиц газа,
![]() ,
,![]() —
удельная теплоемкость (теплоемкость
единицы массы) газа,
—
удельная теплоемкость (теплоемкость
единицы массы) газа,![]() —
плотность газа.
—
плотность газа.
Диффузия - взаимное проникновение соприкасающихся веществ вследствие теплового движения частиц вещества. Диффузия имеет место в газах, жидкостях и твердых телах, причем диффундировать могут как находящиеся в них частицы посторонних веществ, так и собственные частицы (самодиффузия).
Наиболее быстро диффузия происходит в газах, медленнее - в жидкостях, еще медленнее - в твердых телах, что обусловлено характером теплового движения частиц в этих средах.
Проведем описание диффузии примеси одного газа в другом. Для простоты будем считать, что оба газа имеют практически одинаковые молекулы и их суммарная концентрация постоянна и равна величине n:
n = n1 + n2,
где n1 и n2 - концентрации газов.
Введение последнего условия необходимо для того, чтобы в системе не возникало макроскопическое перемешивание газов, а их взаимное проникновение происходило только за счет диффузии.
Пусть концентрация диффундирующего газа n1 зависит только от одной координаты x: n1 = n1(x). Тогда физической величиной, перенос которой в данном случае осуществляется вследствие диффузии, является относительная концентрация газа, которая также зависит только от переменной x:
![]() .
.
Подстановка этого выражения в уравнение переноса дает уравнение диффузии в виде:
![]() .
(1)
.
(1)
Соответственно выражение для потока частиц Jn1 принимает форму:
![]() ,
(2)
,
(2)
где S - площадь, а введенный коэффициент D называется коэффициентом диффузии:
![]() .
(3)
.
(3)
Выражения, аналогичные формулам (1) и (2), могут быть записаны и для второго газа, имеющего концентрацию n2.
Уравнение (3) позволяет также записать формулу, описывающую поток массы. Считая, что молекула газа имеет массу m, умножим на эту величину уравнение (3) и учтем связь величины потока массы Jp1 и потока концентрации частиц Jn1:
Jp1 = mJn1.
Тогда имеем:
![]() ,
,
где 1 = mn - плотность диффундирующего газа.
В системе СИ единицей измерения потока массы Jp1 является кг/с.
С учетом формулы для длины свободного пробега:
![]() ,
,
где - эффективное сечение молекулы газа,
и с учетом выражения для средней скорости:
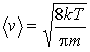 ,
,
выражение для коэффициента диффузии приобретает вид:
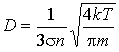 .
.
Как следует из этой формулы, коэффициент диффузии растет с повышением температуры:
![]()
и уменьшается при увеличении концентрации:
![]() .
.
Уменьшение коэффициента диффузии при увеличении концентрации молекул связано с уменьшением длины свободного пробега , что приводит к более частым соударениям диффундирующих частиц с молекулами газа.
