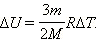- •21.Термодинамические параметры. Равновесные состояния и процессы. Внутренняя энергия идеального газа. Работа газа при изменении его объема. Количество теплоты. Первый закон термодинамики.
- •Частные случаи первого закона термодинамики для изопроцессов
- •22.Теплоемкость.Теплоемкость идеального газа при постоянном давлении и при постоянном объеме. Уравнение Майера
- •23.Применеие первого закона термодинамики при изохорическом, изобарическом, изотермическом процессах. Адиабатический процесс. Уравнение Пуассона. Работа идеального газа при адиабатическом процессе.
- •24.Второй закон термодинамики. Энтропия. Закон возрастания энтропии. Теорема Нернста. Энтропия идеального газа.
- •Энтропия идеальных газов
- •25. Цикл Карно и его кпд для идеального газа.
- •26. Барометрическая формула. Распределение Больцмана.
- •27. Закон Максвелла распределения молекул по абсолютным значениям скоростей. Средняя, средняя квадратичная и наиболее вероятная скорость молекул.
- •28. Столкновение молекул. Эффективное сечение молекулы. Число столкновений молекулы в единицу времени. Длина свободного пробега молекулы.
- •29.Диффузия в газах. Вязкость газов. Теплопроводность газов. Коэффициенты диффузии, вязкости, теплопроводности. Вывод формулы для коэффициента диффузии.
20. Идеальный газ. Основное уравнение мкт. Молякулярно-кинетическое толкование абсолютной температуры. Уравнение Менделеева-Клайперона. Законы идеальных газов. Число степеней свободы молекул. Средняя энергия молекул.
ьс
![]() Тогда
давление газа, оказываемое им на стенку
сосуда,
Тогда
давление газа, оказываемое им на стенку
сосуда,
![]() (1)
Если
газ в объеме V содержит N молекул,
движущихся со скоростями v1,
v2,
..., vN,
то целесообразно рассматривать среднюю
квадратичную скорость
(1)
Если
газ в объеме V содержит N молекул,
движущихся со скоростями v1,
v2,
..., vN,
то целесообразно рассматривать среднюю
квадратичную скорость
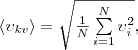 (2)
которая
характеризует всю совокупность молекул
газа. Уравнение (1) с учетом (2) примет
вид
(2)
которая
характеризует всю совокупность молекул
газа. Уравнение (1) с учетом (2) примет
вид
![]() (3)
Выражение
(3) называется основным
уравнением молекулярно-кинетической
теории идеальных газов.
Точный расчет с учетом движения молекул
по всевозможным направлениям дает ту
же формулу.
Учитывая,
что n = N / V, получим
(3)
Выражение
(3) называется основным
уравнением молекулярно-кинетической
теории идеальных газов.
Точный расчет с учетом движения молекул
по всевозможным направлениям дает ту
же формулу.
Учитывая,
что n = N / V, получим
![]() (4)
или
(4)
или
![]() (5)
где
Е — суммарная кинетическая энергия
поступательного движения всех молекул
газа.
Так
как масса газа m=Nm0,
то уравнение (4) можно переписать в
виде
(5)
где
Е — суммарная кинетическая энергия
поступательного движения всех молекул
газа.
Так
как масса газа m=Nm0,
то уравнение (4) можно переписать в
виде
![]() Для
одного моля газа m=М (М — молярная масса),
поэтому
Для
одного моля газа m=М (М — молярная масса),
поэтому
![]() где
Vm —
молярный объем. С другой стороны, по
уравнению Менделеева-Клапейрона ,
pVm=RT.
Таким образом,
где
Vm —
молярный объем. С другой стороны, по
уравнению Менделеева-Клапейрона ,
pVm=RT.
Таким образом,
![]() откуда
откуда
![]() (6)
Так
как M=m0NA,
где m0 —
масса одной молекулы, a NA —
постоянная Авогадро, то из уравнения
(6) следует, что
(6)
Так
как M=m0NA,
где m0 —
масса одной молекулы, a NA —
постоянная Авогадро, то из уравнения
(6) следует, что
![]() (7)
где
k=R/NA —
постоянная Больцмана. что при комнатной
температу¬ре молекулы кислорода имеют
среднюю квадратичную скорость 480 м/с,
водорода — 1900 м/с. При температуре
жидкого гелия те же скорости будут
соответственно 40 и 160 м/с.
Средняя
кинетическая энергия поступательного
движения одной молекулы идеального
газа
(7)
где
k=R/NA —
постоянная Больцмана. что при комнатной
температу¬ре молекулы кислорода имеют
среднюю квадратичную скорость 480 м/с,
водорода — 1900 м/с. При температуре
жидкого гелия те же скорости будут
соответственно 40 и 160 м/с.
Средняя
кинетическая энергия поступательного
движения одной молекулы идеального
газа
![]() (8)
(использовали
формулы (5) и (7)) прямо пропорциональна
термодинамической температуре и зависит
только от нее. Из этого уравнения видно,
что при Т=0 <ε0>=0,
т. е. при 0 К прекращается поступательное
движение молекул газа, а значит, его
давление равно нулю. Таким образом,
термодинамическая температура есть
мера средней кинетической энергии
поступательного движения молекул
идеального газа, и формула (8) раскрывает
молекулярно-кинетическое толкование
температуры.
(8)
(использовали
формулы (5) и (7)) прямо пропорциональна
термодинамической температуре и зависит
только от нее. Из этого уравнения видно,
что при Т=0 <ε0>=0,
т. е. при 0 К прекращается поступательное
движение молекул газа, а значит, его
давление равно нулю. Таким образом,
термодинамическая температура есть
мера средней кинетической энергии
поступательного движения молекул
идеального газа, и формула (8) раскрывает
молекулярно-кинетическое толкование
температуры.
Физическое
состояние массы газа определяется тремя
термодинамическими параметрами:
давлением р, объемом V и температурой
Т. Между этими параметрами существует
определенная связь, называемая уравнением
состояния,
задаваемая в общем виде дается
выражением
![]() где
каждая из переменных является функцией
двух других.
Французский
инженер и физик Б. Клапейрон (1799—1864)
получил уравнение состояния идеального
газа, объединив законы Бойля—Мариотта
и Гей-Люссака. Пусть данная масса газа
занимает объем V1,
образует давление р1 и
находится при температуре T1.
В другом произвольном состоянии масса
газа описывается параметрами р2,
V2,
T2 (рис.
1). Переход из состояния 1 в состояние 2
осуществляется в виде двух процессов:
1) изотермического (изотерма 1–1'), 2)
изохорного (изохора 1'–2).
где
каждая из переменных является функцией
двух других.
Французский
инженер и физик Б. Клапейрон (1799—1864)
получил уравнение состояния идеального
газа, объединив законы Бойля—Мариотта
и Гей-Люссака. Пусть данная масса газа
занимает объем V1,
образует давление р1 и
находится при температуре T1.
В другом произвольном состоянии масса
газа описывается параметрами р2,
V2,
T2 (рис.
1). Переход из состояния 1 в состояние 2
осуществляется в виде двух процессов:
1) изотермического (изотерма 1–1'), 2)
изохорного (изохора 1'–2).
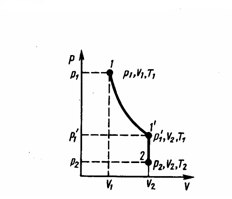
Рис.1
В
соответствии с законами Бойля — Мариотта
и Гей-Люссака запишем:
![]() (1)
(1)
![]() (2)
Исключив
из уравнений (1) и (2) получим
(2)
Исключив
из уравнений (1) и (2) получим
![]() Так
как состояния 1 и 2 были выбраны произвольно,
то для данной массы газа величина pV/T
остается постоянной, т. е.
Так
как состояния 1 и 2 были выбраны произвольно,
то для данной массы газа величина pV/T
остается постоянной, т. е.
![]() (3)
Выражение
(3) является уравнением
Клапейрона,
в котором В — газовая постоянная, которая
различна для разных газов.
Русский
ученый Д. И. Менделеев (1834—1907) сопоставил
уравнение Клапейрона с законом Авогадро,
отнеся уравнение (3) к одному молю,
использовав молярный объем Vm.
По закону Авогадро, при одинаковых р и
Т моли всех газов занимают одинаковый
молярный объем Vm,
поэтому постоянная В будет равной для
всех газов. Эта общая для всех газов
постоянная обозначается R и называетсямолярной
газовой постоянной.
Уравнению
(3)
Выражение
(3) является уравнением
Клапейрона,
в котором В — газовая постоянная, которая
различна для разных газов.
Русский
ученый Д. И. Менделеев (1834—1907) сопоставил
уравнение Клапейрона с законом Авогадро,
отнеся уравнение (3) к одному молю,
использовав молярный объем Vm.
По закону Авогадро, при одинаковых р и
Т моли всех газов занимают одинаковый
молярный объем Vm,
поэтому постоянная В будет равной для
всех газов. Эта общая для всех газов
постоянная обозначается R и называетсямолярной
газовой постоянной.
Уравнению
![]() (4)
удовлетворяет
только идеальный газ, и оно является уравнением
состояния идеального газа,
которая называется также уравнением
Менделеева-Клайперона.
Числовое
значение молярной газовой постоянной
найдем из формулы (4), считая, что моль
газа находится при нормальных условиях
(р0=
1,013•105 Па,
T0=273,15
К, Vm=22,41•10-3 м3/моль):
R=8,31 Дж/(моль•К).
От
уравнения (4) для моля газа можно перейти
к уравнению Менделеева-Клапейрона для
произвольной массы газа. Если при данных
давлении и температуре один моль газа
занимает молярный объем Vm,
то при тех же условиях масса m газа займет
объем V= (m/М)Vm,
где М — молярная масса (масса одного
моля газа). Единица молярной массы —
килограмм на моль (кг/моль). Уравнение
Клапейрона — Менделеева для массы m
газа
(4)
удовлетворяет
только идеальный газ, и оно является уравнением
состояния идеального газа,
которая называется также уравнением
Менделеева-Клайперона.
Числовое
значение молярной газовой постоянной
найдем из формулы (4), считая, что моль
газа находится при нормальных условиях
(р0=
1,013•105 Па,
T0=273,15
К, Vm=22,41•10-3 м3/моль):
R=8,31 Дж/(моль•К).
От
уравнения (4) для моля газа можно перейти
к уравнению Менделеева-Клапейрона для
произвольной массы газа. Если при данных
давлении и температуре один моль газа
занимает молярный объем Vm,
то при тех же условиях масса m газа займет
объем V= (m/М)Vm,
где М — молярная масса (масса одного
моля газа). Единица молярной массы —
килограмм на моль (кг/моль). Уравнение
Клапейрона — Менделеева для массы m
газа
![]() (5)
где ν =
m/M — количество вещества.
Часто
пользуются несколько иной формой
уравнения состояния идеального газа,
вводя постоянную
Больцмана:
k=R/NA=1,38•10-23 Дж/К
Исходя
из этого уравнение состояния (4) запишем
в виде
(5)
где ν =
m/M — количество вещества.
Часто
пользуются несколько иной формой
уравнения состояния идеального газа,
вводя постоянную
Больцмана:
k=R/NA=1,38•10-23 Дж/К
Исходя
из этого уравнение состояния (4) запишем
в виде
![]() где
NA/Vm =
n — концентрация молекул (число молекул
в единице объема). Таким образом, из
уравнения
где
NA/Vm =
n — концентрация молекул (число молекул
в единице объема). Таким образом, из
уравнения
![]() (6)
мы
видим, что давление идеального газа при
данной температуре прямо пропорционально
концентрации его молекул (или плотности
газа). При одинаковых давлении и
температуре любой газ содержат в единице
объема одинаковое число молекул. Число
молекул, которые содержатся в 1 м3 газа
при нормальных условиях, называется числом
Лошмидта:
NL =
p0/(kT0)
= 2,68•1025 м-3
(6)
мы
видим, что давление идеального газа при
данной температуре прямо пропорционально
концентрации его молекул (или плотности
газа). При одинаковых давлении и
температуре любой газ содержат в единице
объема одинаковое число молекул. Число
молекул, которые содержатся в 1 м3 газа
при нормальных условиях, называется числом
Лошмидта:
NL =
p0/(kT0)
= 2,68•1025 м-3
21.Термодинамические параметры. Равновесные состояния и процессы. Внутренняя энергия идеального газа. Работа газа при изменении его объема. Количество теплоты. Первый закон термодинамики.
Термодинамическими величинами называют физические величины, применяемые при описании состояний и процессов в термодинамических системах.
Термодинамика рассматривает эти величины как некоторые макроскопические параметры и функции, присущие системе, но не связанные с её микроскопическим устройством. Вопросы микроскопического устройства изучает статистическая физика.
Функции состояния
Функции состояния зависят только от текущего состояния системы и не зависят от пути, по которому система пришла в это состояние.
Функции состояния в термодинамике включают:
температуру,
давление,
объём,
энтропию,
а также термодинамические потенциалы.
В зависимости от выбранной модели некоторые из этих величин, строго говоря, могут быть не функциями, а независимыми переменными.
Эти величины не являются независимыми. Связь между термодинамическими параметрами для конкретной системы называется уравнением состояния.
В случае, если известно каноническое уравнение состояния, задание любой пары параметров из следующих:
энтропия и объём,
энтропия и давление,
температура и объём,
температура и давление,
позволяет вычислить остальные два параметра.
Функции процесса
Функции процесса зависят не только от текущего состояния системы, но также и от пути, по которому система пришла в данное состояние.
Функции процесса в термодинамике включают:
количество теплоты и
термодинамическую работу.
Эти величины, однако, могут быть «превращены» в функции состояния с помощью интегрирующего множителя:
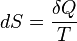 ,
где
,
где 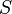 (энтропия)
— функция состояния.
(энтропия)
— функция состояния.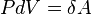 ,
где
,
где 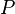 (давление)
и
(давление)
и 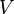 (объём)
— функции состояния.
(объём)
— функции состояния.
Для вычисления внутренней энергии одноатомного идеального газа необходимо среднекинетическую энергию движения одного атома умножить на число атомов в рассматриваемом объеме.
Число атомов N, в свою очередь, может быть выражено через число Авогадро NA и количество вещества n = m / M.
|
Произведение двух постоянных величин – постоянной Больцмана и числа Авогадро равно универсальной газовой постоянной:
|
Таким образом, после ряда преобразований получаем, что, для одноатомного идеального газа внутренняя энергия прямо пропорциональна его абсолютной температуре, массе, и обратно пропорциональна молярной массе. Так как газ одноатомный, коэффициент пропорциональности между этими величинами равен 3/2.
|
Изменение внутренней энергии одноатомного идеального газа при переходе из одного состояния в другое будет равно:
|
Существенно, что изменение этой величины при переходе газа из состояния с температурой Т1 в состояние с температурой Т2определяется только его начальным и конечным состоянием и не зависит от способа перехода из одного состояния в другое.
Q -
энергия, которую тело теряет или
приобретает при передаче тепла.
Формула
количества теплоты зависит
от протекающего процесса.
Формулы
количества теплоты при некоторых
процессах:
![]() Количество
теплоты при
нагревании и охлаждении.
Количество
теплоты при
нагревании и охлаждении.
![]() Количество
теплоты при плавлении
или кристаллизации.
Количество
теплоты при плавлении
или кристаллизации.
![]() Количество
теплоты при кипении,
испарении жидкости и
конденсации пара.
Количество
теплоты при кипении,
испарении жидкости и
конденсации пара.
![]() Количество
теплоты при сгорании
топлива.
Количество
теплоты всегда передается от
более горячих тел к
более холодным до
достижения ими одинаковой температуры
(теплового равновесия), если нет иных
процессов, кроме теплопередачи.
В
замкнутой системе тел выполняется
уравнение теплового балланса: Q1 +
Q2 +
... = 0 -
количество теплоты, которое теряют
горячие тела, равно количеству тепла,
получаемому холодными.
Полезные
формулы:
Количество
теплоты, переданное телу,
идет
на изменение его внутренней энергии
и
на совершение им работы (Первый закон
термодинамики).
Закон
Джоуля-Ленца: в
неподвижном металлическом проводнике
вся энергия электрического
тока превращается
в тепло:
Количество
теплоты при сгорании
топлива.
Количество
теплоты всегда передается от
более горячих тел к
более холодным до
достижения ими одинаковой температуры
(теплового равновесия), если нет иных
процессов, кроме теплопередачи.
В
замкнутой системе тел выполняется
уравнение теплового балланса: Q1 +
Q2 +
... = 0 -
количество теплоты, которое теряют
горячие тела, равно количеству тепла,
получаемому холодными.
Полезные
формулы:
Количество
теплоты, переданное телу,
идет
на изменение его внутренней энергии
и
на совершение им работы (Первый закон
термодинамики).
Закон
Джоуля-Ленца: в
неподвижном металлическом проводнике
вся энергия электрического
тока превращается
в тепло:
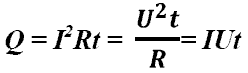 - закон
Джоуля - Ленца.
- закон
Джоуля - Ленца.![]()
Первый закон термодинамики (закон сохранения энергии для тепловых процессов) определяет количественное соотношение между изменением внутренней энергии системы дельта U, количеством теплоты Q, подведенным к ней, и суммарной работой внешних сил A, действующих на систему.
Первый закон термодинамики - Изменение внутренней энергии системы при ее переходе из одного состояния в другое равно сумме количества теплоты, подведенного к системе извне, и работы внешних сил, действующих на нее:
![]()
Первый закон термодинамики - количество теплоты, подведенное к системе, идет на изменение ее внутренней энергии и на совершение системой работы над внешними телами:
![]()