Лекция 02

6

ЛЕКЦИЯ 2

Уравнение поверхностей уровня жидкости, вращающейся вместе с сосудом вокруг вертикальной оси с угловой скоростью ω. Уравнение свободной поверхности уровня.

Пусть имеется сосуд с жидкостью, вращающийся вокруг вертикальной оси с угловой скоростью ω. Найдем уравнение поверхностей уровня для рассматриваемого случая, воспользовавшись уравнением поверхности уровня в дифференциальном виде

.

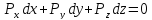На жидкость массой m в окрестностях произвольно взятой точки М действуют внешние массовые силы:

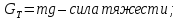
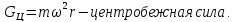Найдем проекции этих сил и суммы проекций единичных массовых сил на оси координат.

Ось x

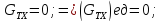
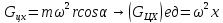Следовательно, сумма проекций единичных массовых сил на ось x будет равна

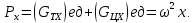
R – радиус сосуда;

r - радиус вращения т. М;

h – глубина погружения т. М от

свободной

поверхности уровня.

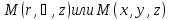
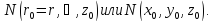
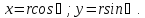
Ось y

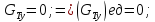
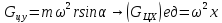
Следовательно, сумма проекций единичных массовых сил на ось y будет равна

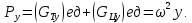Ось z

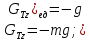
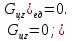Следовательно, сумма проекций единичных массовых сил на ось z будет равна

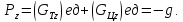
Подставляя найденные значения сумм проекций единичных массовых сил, получим 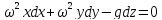. Берем неопределенный интеграл полученного выражения

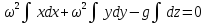
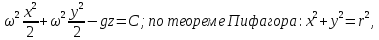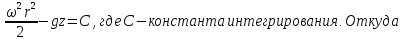
поэтому 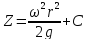– уравнение поверхностей уровня (уравнение семейства параболоидов вращения)

Уравнение свободной поверхности уровня

Рассмотрим вершину параболоида вращения соответствующего свободной поверхности уровня; для нее справедливо: r=0; 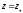; подставляя эти значения в последнее уравнение получим значение константы интегрирования для уравнения свободной поверхности уровня 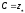, отсюда следует что, уравнением свободной поверхности уровня будет

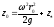
Геометрический смысл 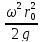– высота подъема ветви параболоида вращения относительно горизонтальной плоскости 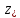для точки на свободной поверхности уровня N(.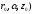

Максимальная высота подъема жидкости в сосуде

H – максимальная высота подъема жидкости параболоида вращения свободной поверхности уровня.

Согласно уравнения свободной поверхности уровня 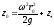для точки на этой поверхности с координатами () связь между Н и R будет определяться уравнением 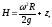. Далее следует заменить через первоначальный уровень жидкости в сосуде 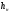(при ).

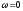– объем жидкости в сосуде, который находится в состоянии абсолютного покоя;

- объем жидкости в сосуде, который находится в состоянии относительного покоя; в силу закона сохранения объема жидкости получают

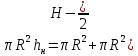
Откуда

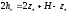или 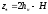. Подставляя полученное выражение в ранее найденное для максимальной высоты подъема жидкости, получим

, откуда

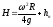
– максимальная высота подъема жидкости в сосуде

Закон распределения давления внутри жидкости, вращающейся вместе с сосудом вокруг вертикальной оси с угловой скоростью ω.

Закон Паскаля, полученный ранее для случая абсолютного покоя жидкости, справедлив и для случая относительного покоя в любых его формах в том числе и для вращающегося сосуда; здесь h есть сумма высоты подъема ветви параболоида вращения над плоскостью 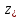и расстояния между горизонтальными плоскостями 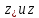. Т.е. .

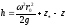Определение силы давления жидкости на плоскую стенку сосуда и на дно сосуда (без вывода).

РИСУНОК

F – площадь смоченной боковой стенки сосуда;

h_ц – глубина погружения центра масс площади F;

точка ЦМ – центр масс площади F;

точка ЦД – центр давления, точка приложения равнодействующей силы давления.

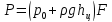– сила полного давления на боковую стенку сосуда (сила атмосферного давления + сила гидростатического давления жидкости).

Сила полного давления на дно сосуда может быть определена по формуле

Определение точки приложения силы полного давления (координаты центра давления 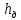). Без вывода.

I₀ – момент инерции площади, относительно центральной оси (ось, которая проходит через центр масс площади F)

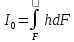
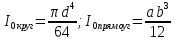, где a – основание прямоугольника, b – высота.

Элементы кинематики жидкости

(Основная теорема кинематики – теорема Коши-Гельмгольца. Траектория жидкостной частицы. Линии тока. Элементарная струйка. Трубка тока. Поток жидкости. Живое сечение потока. Смоченный периметр. Гидравлический радиус. Эквивалентный диаметр).

В кинематике изучают движение жидкости с точки зрения геометрии, без учета ее массы и сил, определяющих это движение

Основная теорема кинематики – теорема Коши-Гельмгольца. В этой теореме доказывают, что скорость перемещения жидкостной частицы складывается из трех скоростей:

– поступательная скорость;

– деформационная скорость;

Изменение прямых углов одной из граней за время

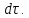
– вращательная скорость.

Траектория жидкостной частицы – это путь, пройденный жидкостной частицей за некоторый промежуток времени (S).

Линиями тока называют совокупность жидкостных частиц, векторы скоростей которых касательны к ней в данный момент времени.

Элементарная струйка. Трубка тока.

Если в движущейся жидкости в поперечном сечении выделить элементарную площадку dS и через все точки провести линии тока для данного момента времени, то получается объемный пучок линий тока, который называется элементарной струйкой, а ее боковая поверхность – поверхность трубки тока.

Поток жидкости – это совокупность элементарных струек жидкости, текущих в данном русле.

Живое сечение потока – это поверхность, проведенная через данную точку в пределах потока, перпендикулярная линиям тока.

Смоченным периметром называют длину линии, по которой жидкость в данном живом сечении соприкасается с руслом.

Гидравлический радиус (для канала с произвольным сечением) – это отношение площади живого сечения к смоченному периметру.

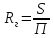
Для круглой трубы гидравлический радиус равен:

где d – смоченный периметр

Гидравлический радиус в два раза меньше геометрического.

Эквивалентный диаметр (для канала произвольного сечения) принимается равным:

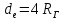
Плавно изменяющееся движение жидкости – это такое движение, при котором кривизна струек мала, угловое расхождение между отдельными струйками не велико, живое сечение потока плоское, перпендикулярно оси потока.

Расход жидкости – это объем жидкости, протекающей через поперечное сечение потока в единицу времени.

Средней скоростью в данном сечении потока называется такая фиктивная, но одинаковая во всех точках данного сечения скорость, при которой через сечение проходит то же количество жидкости, какое и при действительном распределении скоростей.