Лекция 06

6

Лекция 6

Расчет газопровода.

При движении газов (они сжимаемы) их плотность изменяется в силу изменения давления. Одновременно, вследствие расширения газа при уменьшении давления в направлении движения увеличивается объемный расход; поэтому для газопроводов, следует оперировать не объемным расходом, а массовым расходом, поскольку для стационарного движения именно массовый расход остается неизменным.

Пусть имеется газопровод длиной l, диаметром D. По газопроводу под действием разности давлений p₁ – p₂ движется газ, температура которого неизменна на всем пути следования. Выделим на расстоянии x от входа в газопровод элементарный участок dx, для которого характерны текущие значения давления p, плотности , скорости w газа. При этом указанные параметры переменны по всей длине газопровода.

Запишем уравнение Бернулли для участка dx газопровода (запись уравнения Бернулли в интегральной форме для всего участка, как это было для несжимаемой жидкости, невозможна, так как газ сжимаем).

В этом уравнении не все слагаемые равнозначны. Последнее обусловлено низкими значениями плотностей газа (на 2 – 3 порядка ниже плотности жидкости). По этой причине слагаемыми 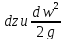можно пренебречь в сравнении с . Потерянный напор по уравнению Дарси – Вейсбаха равен 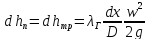(местные потери отсутствуют). С учетом сказанного уравнение Бернулли в дифференциальном виде упростится до выражения

Откуда

или

Выразим переменную по длине газопровода скорость w через массовый расход (постоянный по длине) согласно уравнению массового расхода где 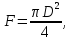откуда , тогда

(1)

Перенесем 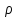в левую часть и установим связь 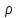и p. Будем считать, что в относительно небольшом диапазоне давлений p₁ – p₂ газ ведет себя как идеальный, тогда согласно уравнению Менделеева – Клайперона

где R – газовая постоянная (); М – молярная масса газа. Отсюда

. Подставим это значение в (1)

Пренебрегая влиянием Re на , интегрируем последнее уравнение от p₁ до p₂ и, соответственно от 0 до l, получаем, избавляясь от знака “минус» меняя пределы интегрирования в левой части

(2)

В случае задачи эксплуатации (определение массового расхода газа при известных значениях перепада давления и геометрических размеров газопровода) последняя формула трансформируется до вида

(3)

Расчет начинают с выбора скорости в «разумных пределах» (для газа: 5 – 30 м/с); далее – круги итерации с сопоставлением стартовых G(н) и рассчитанных G(к) значений потоков

Алгоритм

w G(н) Re G(к)

или следующее приближ. или готовый результат

Истечение жидкости из отверстия в дне сосуда при постоянном напоре. Скорость истечения. Расход. Как увеличить расход? Насадки (цилиндрическая K_р=0,82; коническая K_р=0,963; коноидальная K_р=0,98)

Пусть имеется вертикальный, цилиндрический сосуд. В дне сосуда имеется отверстие.

P₁

1

w₁

V

D

h

A

Z₁

V,w₂

2

Z₂

P₂

0

0

На участке местного сопротивления (отверстие с острыми кромками) наблюдается нестационарный характер движения жидкости (cм. «местные сопротивления»)

После сечения 2 наблюдается стационарное движение жидкости (линии тока параллельны друг другу). Расстояние от дна сосуда до 2 го сечения потока жидкости составляет 0,5  1 от диаметра отверстия d_о.

Отверстие с острыми кромками – это такое отверстие, для которого можно пренебречь путевыми потерями (потерями на трение).

Запишем уравнение Бернулли для указанных двух сечений:

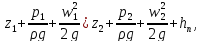
z₁ – z₂ = h – уровень жидкости в сосуде

Запишем уравнение сплошности

Так как , то и .

Следовательно, потери на трение вдоль стенок сосуда равны нулю, т.е. и

Уравнение Бернулли преобразуется до вида

или

, где - коэффициент местного сопротивления при протекании жидкости через отверстие.

В результате подстановки получаем

или, опуская индекс «2» откуда

Здесь коэффициент скорости истечения, который характеризует замедление течения жидкости по причине гидравлического сопротивления в отверстии; для отверстия с острыми кромками

Выведем формулу для расхода жидкости при постоянном напоре:

или, опуская индекс, , где f – сечение струи. Сечение струи связано с сечением отверстия формулой 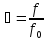, где - коэффициент сжатия струи. Отсюда

. Произведение называется коэффициентом расхода при истечении и обозначается символом К_p. Тогда

. При уравнение расхода преобразуется до вида

. Коэффициент расхода для отверстия с острыми кромками составляет 0,62.

Для увеличения расхода отверстие можно снабдить насадками.

1. Цилиндрическая насадка _р=0,82

2. Коническая насадка _р=0,963

3. Коноидальная насадка повторяет форму истечения струи, которая уже не отрывается от стенок. _р=0,98

Время частичного или полного опорожнения сосуда произвольной формы (истечение при переменном напоре)

Пусть имеется сосуд произвольной формы с отверстием в дне. Рассмотрим частичное опорожнение жидкости. Пусть при

. Для произвольного момента времени уровень жидкости в сосуде будет равен z (z – текущий напор).

Составим ОБС по объему жидкости за элементарный промежуток времени начиная от произвольного момента времени для выделенного контура (на участке z)

Пр – Ух = Нак

Пр = 0; Ух = ; (принимая, что на участке сосуда высотой ). После подстановки в ОБС получим

.

Разделяя переменные и интегрируя от 0 до и от до , получим

. (1)

В случае полного опорожнения сосуда 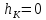, тогда формула (1) преобразуется до вида

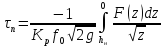. (2)

В случае сосуда постоянного поперечного сечения по высоте F выносится за знак интеграла и последующее интегрирование дает следующие результаты:

при частичном опорожнении

(3)

при полном опорожнении

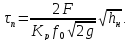(4)