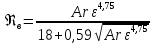Лекция 08
.docx
Лекция 8
Скорость начала псевдоожижения. Формула Тодеса.
Согласно
ранее рассмотренному материалу
сопротивление неподвижного слоя д.м. и
сопротивление ПС д.м. при скорости ОА
равной скорости начала псевдоожижения
будут иметь одинаковые значения, т.е.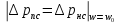 .
.
Подставляя выражения для сопротивлений НС и ПС., получим
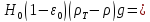
 После упрощения
После упрощения
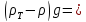
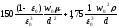 . Умножим обе части полученного выражения
на
. Умножим обе части полученного выражения
на 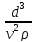
. В результате получим

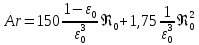 , где
, где
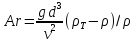 - критерий Архимеда, который показывает
соотношение между силами препятствующими
процессу псевдоожижения и способствующими
оному;
- критерий Архимеда, который показывает
соотношение между силами препятствующими
процессу псевдоожижения и способствующими
оному;
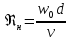 - критерий Рейнольдса, который характеризует
режим движения ОА.
- критерий Рейнольдса, который характеризует
режим движения ОА.
Пусть
режим движения турбулентный, тогда
первый член правой части полученного
выражения будет равен нулю. Откуда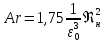 .
Найдем зависимость критерия Рейнольдса
от критерия Архимеда
.
Найдем зависимость критерия Рейнольдса
от критерия Архимеда
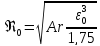 .
Заменим одно из значений критерия
Рейнольдса полученным выражением в
общем уравнении
.
Заменим одно из значений критерия
Рейнольдса полученным выражением в
общем уравнении
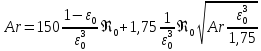 . Найдем общую зависимость критерия
Рейнольдса от критерия Архимеда,
подставляя значение порозности равное
0,4
. Найдем общую зависимость критерия
Рейнольдса от критерия Архимеда,
подставляя значение порозности равное
0,4
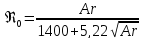 (формула Тодеса). Формула Тодеса позволяет
получить значение скорости начала
псевдоожижения при известном значении
критерия Архимеда.
(формула Тодеса). Формула Тодеса позволяет
получить значение скорости начала
псевдоожижения при известном значении
критерия Архимеда.
Скорость уноса. Скорость осаждения одиночной шарообразной частицы. Универсальная формула Тодеса.
Скоростью
уноса твердых частиц из слоя называют
такую скорость ОА., при которой эти
частицы начинают покидать слой. Скорость
ОА
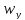 зависит от многих факторов: размера и
формы частиц; гранулометрического
состава; взаимного влияния частиц
(значения порозности
зависит от многих факторов: размера и
формы частиц; гранулометрического
состава; взаимного влияния частиц
(значения порозности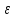 ); высоты ПС; интенсивности барботажа
газовых пузырей; конструктивного
оформления аппарата. Учесть влияние
совокупности этих фаторов невозможно.
Поэтому упрощают задачу и ищут не
скорость уноса, а ее приближенную оценку,
а именно, скорость витания единичной
сферической частицы
); высоты ПС; интенсивности барботажа
газовых пузырей; конструктивного
оформления аппарата. Учесть влияние
совокупности этих фаторов невозможно.
Поэтому упрощают задачу и ищут не
скорость уноса, а ее приближенную оценку,
а именно, скорость витания единичной
сферической частицы
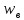 .
.
Витанием называют состояние частицы, когда ее вес полностью уравновешен выталкивающей (архимедовой) силой и силой воздействия потока среды.
Чаще всего равновесие указанных сил рассматривается в двух вариантах:
а)
частица поддерживается выталкивающей
силой и силой воздействия потока среды
в неподвижном состоянии относительно
стенок аппарата,
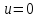 ;
тогда скорость газа равна
;
тогда скорость газа равна
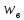 ;
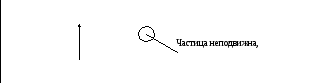
;

б)
частица падает в неограниченном объеме
неподвижной среды (газа, жидкости); тогда
скорость установившегося движения
частицы u =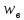 (в рамках рассмотрения процессов
осаждения такую скорость называют
скоростью осаждения, а не скоростью
витания).
(в рамках рассмотрения процессов
осаждения такую скорость называют
скоростью осаждения, а не скоростью
витания).
Анализ проведем для случая а), но результаты этого анализа будут справедливы и для всех остальных случаев.
Пусть
сферическая частица диаметром d
и плотностью
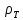 поддерживается указанными выше силами
в неподвижном состоянии при плотности
среды
поддерживается указанными выше силами
в неподвижном состоянии при плотности
среды
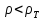 .
Тогда скорость среды равна
.
Тогда скорость среды равна
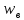 .
Чтобы частица находилась в равновесии,
необходимо равенство действующих на
нее сил (см. рис.): веса частицы
.
Чтобы частица находилась в равновесии,
необходимо равенство действующих на
нее сил (см. рис.): веса частицы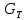 ,
выталкивающей (архимедовой) силы
,
выталкивающей (архимедовой) силы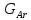 и воздействия потока среды РП.
При
и воздействия потока среды РП.
При
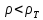 очевидно:
очевидно:
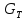 =
=
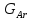 + РП (1)
+ РП (1)

Здесь
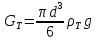 ,
,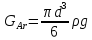 .
При движении потока среды относительно
частицы возникает гидравлическое
сопротивление, которое можно трактовать
как местное и записать в привычной форме
.
При движении потока среды относительно
частицы возникает гидравлическое
сопротивление, которое можно трактовать
как местное и записать в привычной форме
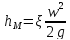 .
Коэффициент
.
Коэффициент
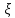 при обтекании тела называют коэффициентом
лобового сопротивления. В терминах
перепада давления это сопротивление
запишется в виде или
при обтекании тела называют коэффициентом
лобового сопротивления. В терминах
перепада давления это сопротивление
запишется в виде или
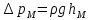 ,
а сила сопротивления, (т.е сила воздействия
потока на частицу) – как
,
а сила сопротивления, (т.е сила воздействия
потока на частицу) – как
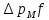 ,
где
,
где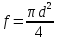 - поперечное сечение сферической
частицы. Тогда, имея в виду, что скорость,
необходимая для поддержания частицы в
равновесии, есть скорость витания
- поперечное сечение сферической
частицы. Тогда, имея в виду, что скорость,
необходимая для поддержания частицы в
равновесии, есть скорость витания
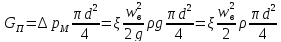 .
Подставляя выражения сил в общее
уравнение (1), получим
.
Подставляя выражения сил в общее
уравнение (1), получим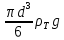 =
=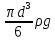 +
+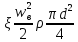 .
После упрощений
.
После упрощений
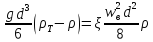 .
.
Поделив
обе части равенства на
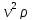 ,
перейдем к обобщенным переменным
,
перейдем к обобщенным переменным
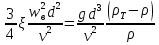 или
или
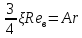 ,
(2)
,
(2)
где
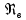 - критерий Рейнольдса для скорости
витания;
- критерий Рейнольдса для скорости
витания;
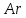 - критерий Архимеда.
- критерий Архимеда.
Значение
коэффициента
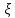 зависит от режима обтекания сферы
потоком. Теоретический анализ показывает,
что для любого режима обтекания сферы
потоком справедливо
зависит от режима обтекания сферы
потоком. Теоретический анализ показывает,
что для любого режима обтекания сферы
потоком справедливо
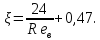 При малых
При малых
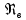 доминирует первое слагаемое, при больших
– второе.
доминирует первое слагаемое, при больших
– второе.
Подставим
значение
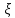 в уравнение (2)
в уравнение (2)
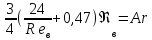 .
Получим
.
Получим
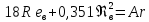 . (3)
. (3)
При автомодельном турбулентном режиме первое слагаемое мало, так что
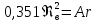 ,
откуда
,
откуда
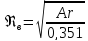 .
Подставив это значение
.
Подставив это значение
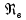 во второе слагаемое левой части уравнения
(3), получим
во второе слагаемое левой части уравнения
(3), получим
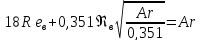 .
После упрощений
.
После упрощений
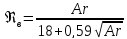 . (4)
. (4)
Это
выражение получило название формулы
Тодеса для скорости витания. Первое
слагаемое в знаменателе представляет
собой ламинарную составляющую, второе
– турбулентную. В случае ламинарного
режима
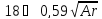 и тогда формула Тодеса превращается в
известную формулу Стокса
и тогда формула Тодеса превращается в
известную формулу Стокса
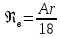 .
.
Для переходного режима оба слагаемых сопоставимы по величине.
В случае турбулентного режима получаем формулу Ньютона
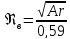 .
.
Скорость витания несферических частиц вычисляется с использованием поправочных коэффициентов.
Формула
Тодеса (4) справедлива для
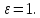
В случае группового витания (стесненного витания или стесненного осаждения – случай б) справедлива универсальная формула Тодеса для диапазона изменения порозности от 0,4 до 1.