Файлы по комбинаторике / Kombin_2new

Біном Ньютона.

Перевірка лекційного матеріалу (фронтальне опитування)

• Яка рівність називається формулою Бінома Ньютона

• Як називають коефіцієнти в правій частині розкладу

• Перерахуйте властивості бінома Ньютона

Завдання 1. Запишіть розклад бінома .

.

.

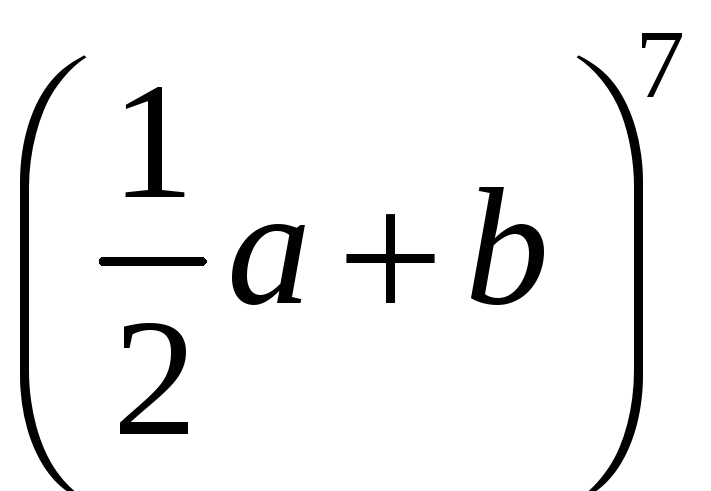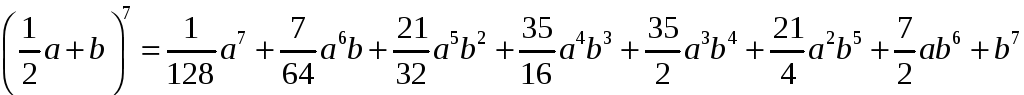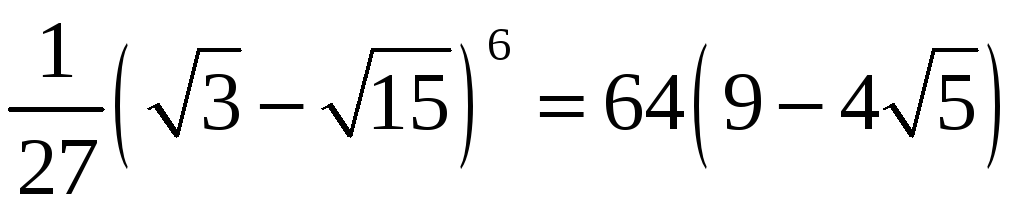Завдання 2. Знайти середній член розкладу .

Розв’язання. Розклад має 13 членів. Тому середнім є - сьомий член. Маємо .

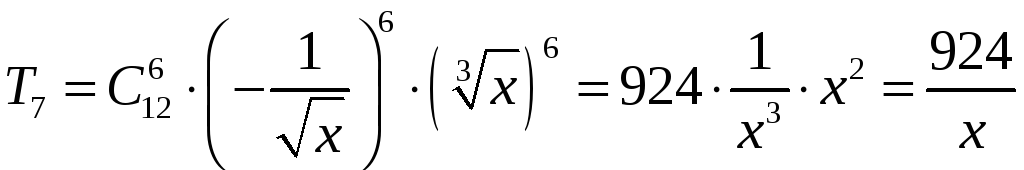Завдання 3. Знайти середній член розкладу бінома 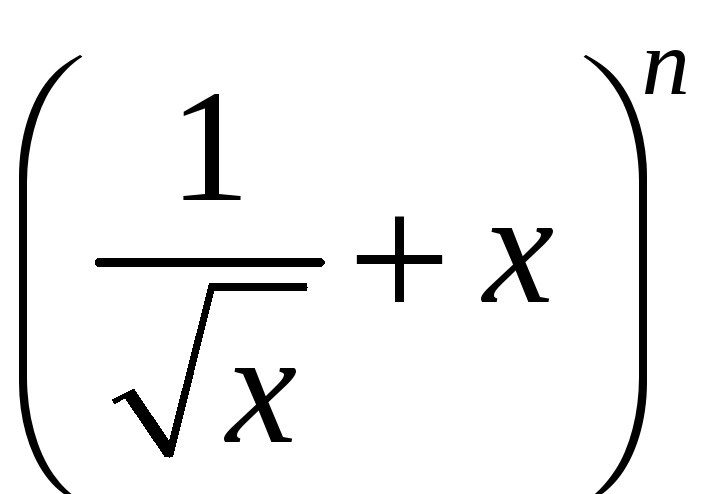, якщо сума біноміальних коефіцієнтів цього розкладу дорівнює 256.

Розв’язання. Використавши властивість бінома, що сума біноміальних коефіцієнтів розкладу дорівнює . Розв’язавши показникові рівняння знайдемо . Отже біном прийме вид . Розклад має 9 членів, а тому буде середнім.

.

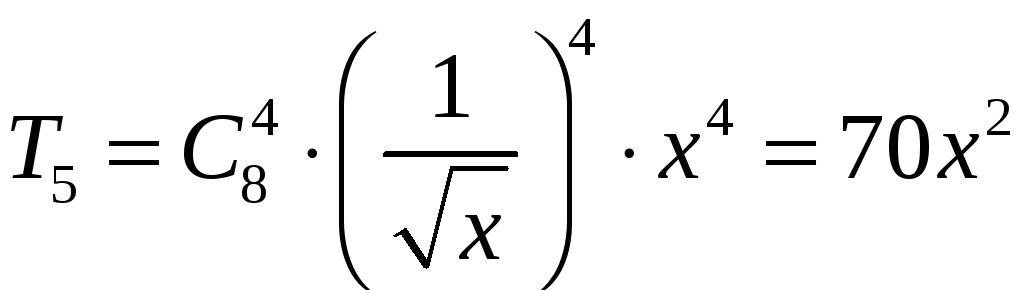Завдання 4. Знайти х, якщо п’ятий член розкладу бінома дорівнює .

Розв’язання. Зауважимо, що . Маємо

, , .

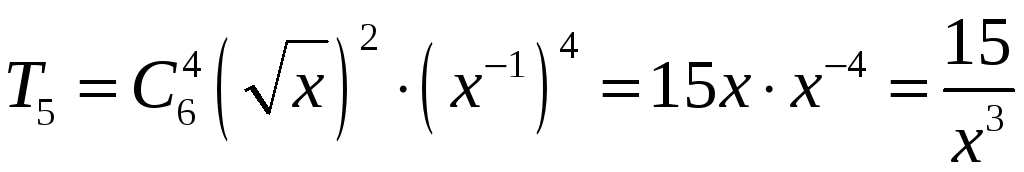
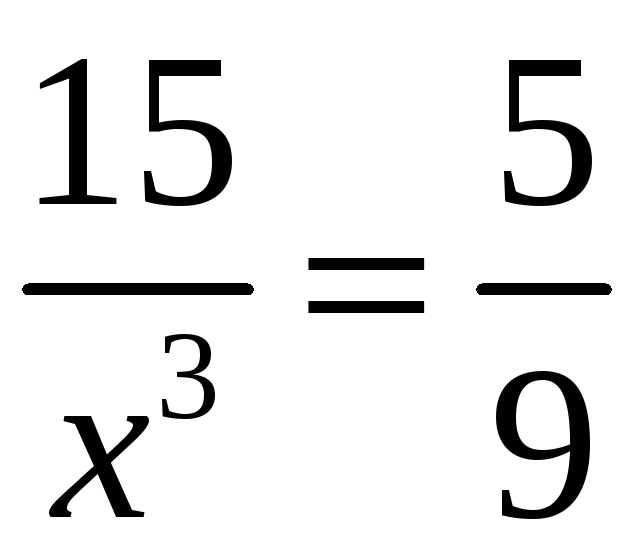Завдання 5. Знайдіть член розкладу , який не містить .

Розв’язання. 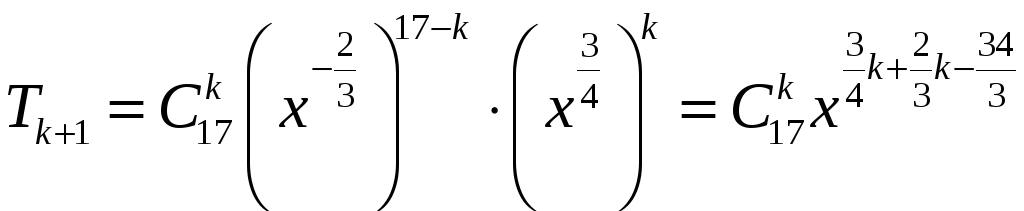. За умовою 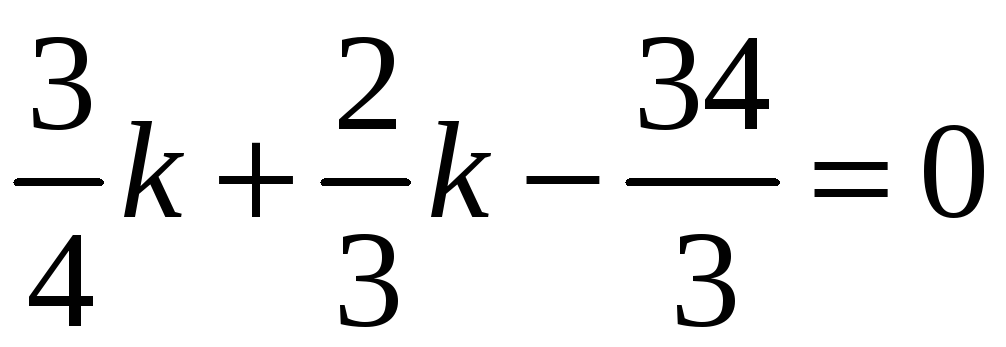, звідки . Отже шуканий член дорівнює .

Завдання 6. Знайти тринадцятий член розкладу 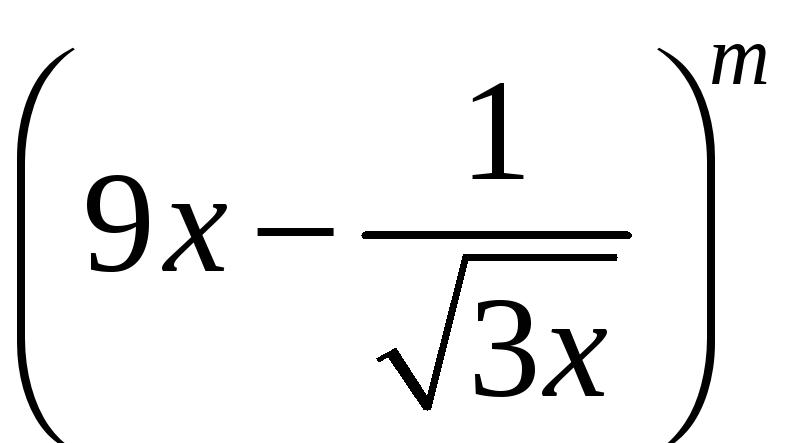біноміальний коефіцієнт третього члена дорівнює 105.

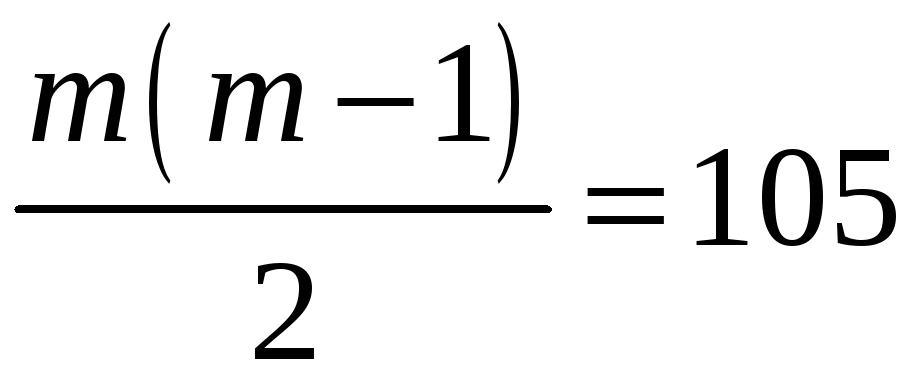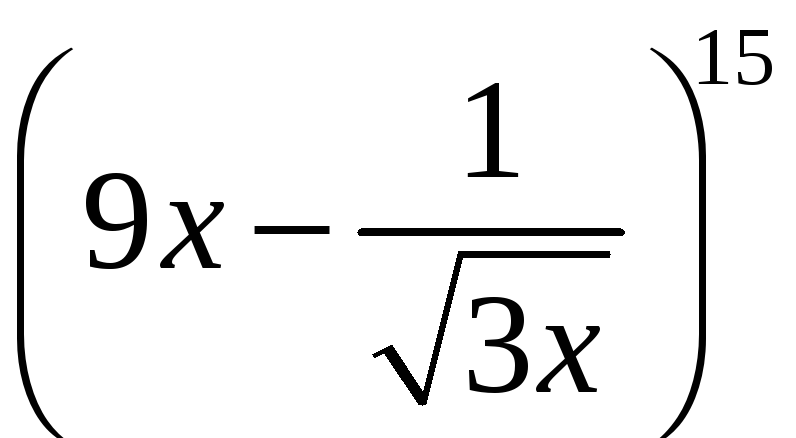Розв’язання. За умовою , тобто , або . Оскільки , то . Маємо розклад . Тоді .

Завдання 7. Знайти коефіцієнт при в розкладі виразу.

Розв’язання. Перетворимо цей вираз так: . Останні члени не виписані, бо вони містять х в степені вище четвертої. Випишемо коефіцієнти при у кожному доданку правої частини і додамо їх. Маємо .

Завдання 8. Знайти суму коефіцієнтів у біноміальному розкладі при довільному натуральному п .

Розв’язання. . Суму коефіцієнтів отримаємо, якщо в розклад підставимо . Отже, шукана сума коефіцієнтів у розкладі дорівнює .

Завдання 9. Знайти раціональні члени в розкладі .

Розв’язання. Загальний член розкладу дорівнює . Необхідно, щоб число було цілим, тобто - парне. Тепер серед парних чисел, менших п'яти, знайдемо таке, щоб число було цілим. Єдиним таким числом є двійка. Отже, , тобто існує єдиний раціональний член цього розкладу .

Завдання 10. При яких значеннях х четвертий доданок розкладу більший за два сусідніх з ним доданки ?

Розв’язання. , , . За умовою Т₄>Т₅,Т₄>Т₃. Маємо систему нерівностей

Враховуючи, що , розділимо обидві нерівності на , маємо .

Звідси .

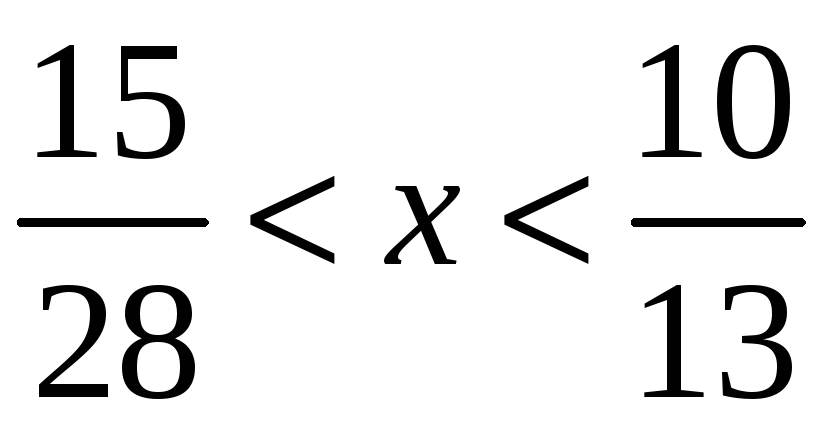Домашнє завдання.

Знайдіть розклад:

1. , 2. , 3., 4. .

5. Знайдіть середній член розкладу бінома .

6. Знайдіть , четвертий член розкладу бінома 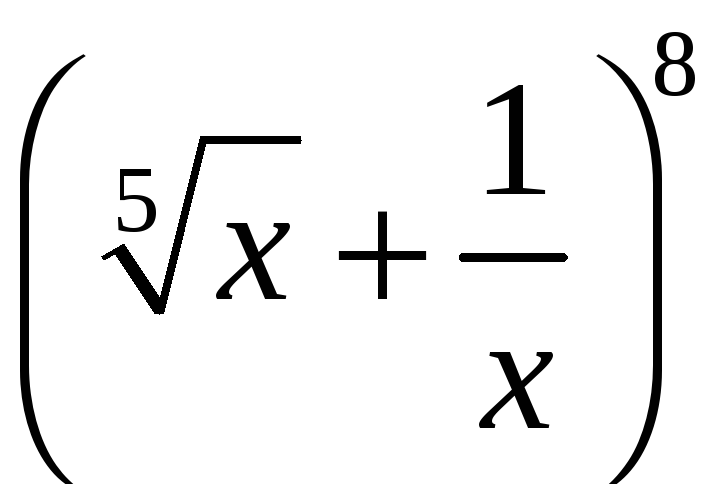дорівнює 56.

7. Знайдіть члени, що не містять , у розкладі .

8. Знайдіть члени, що не містять , у розкладі 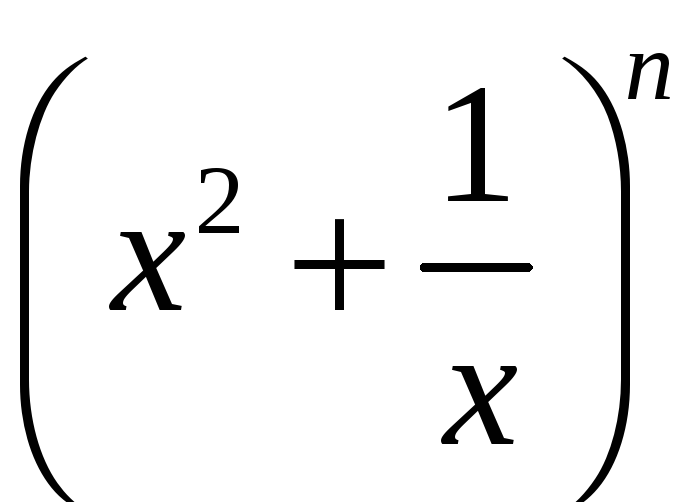, якщо сума коефіцієнтів першого, другого та третього членів дорівнює 46.

9. Знайти член розкладу , що містить .

10. Знайти раціональні члени в розкладі .

11. Скільки є раціональних членів в розкладі біному .

12. при якому значенні другий доданок розкладу більший за два суміжних з ним доданки?

Розв’язання систем рівнянь, що містять комбінаторні вирази.

При розв’язанні системи рівнянь може бути застосований алгоритм розв’язання комбінаторних рівнянь. Але в деяких прикладах будемо відступати від плану, якщо це полегшує розв'язування.

Задача 1. Розв'язати систему рівнянь

Розв'язання. Віднімемо почленно від першого рівняння друге і розділимо результат на п'ять. Дістанемо, що . Підставимо це значення в перше рівняння, одержимо, що . 1) , , . 2) Як відомо, 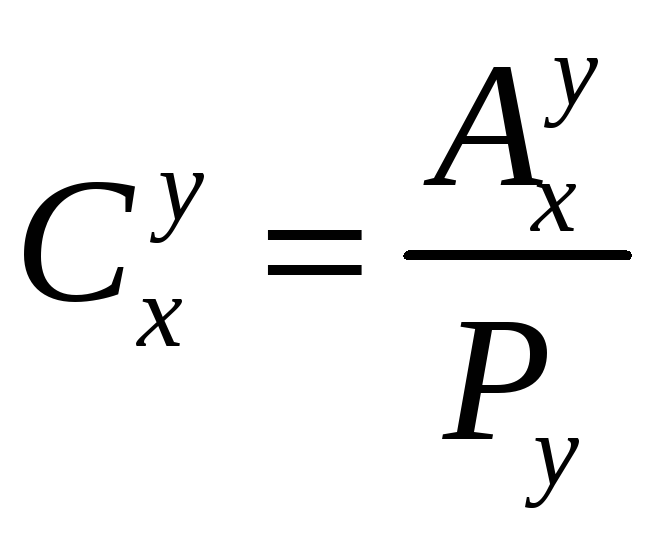, тому 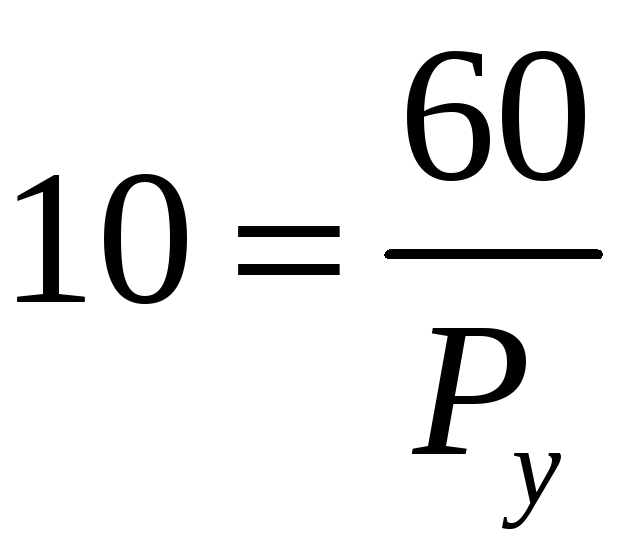, а отже , то . Маємо , тобто . отримаємо що .

Задача 2. Розв'язати систему рівнянь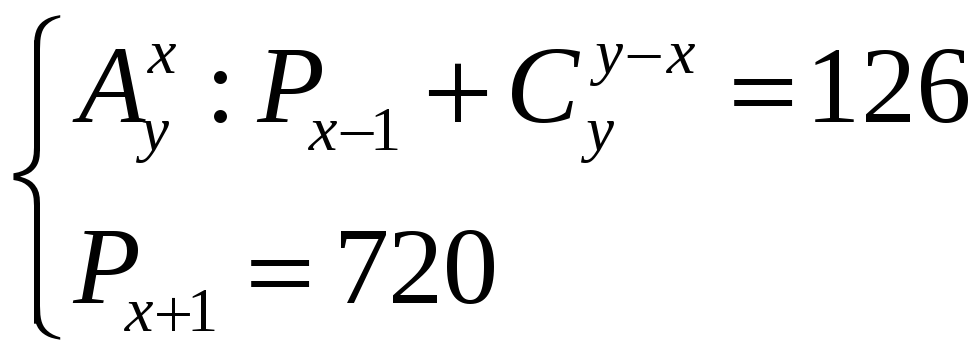

Розв’язання. З другого рівняння системи маємо, що , тобто , . Тоді . 1). 2).

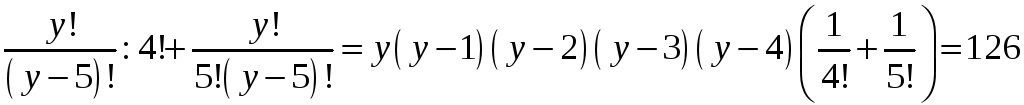3) Звідси дістанемо, що , тобто . Отже,

Задача 3. Розв'язати систему рівнянь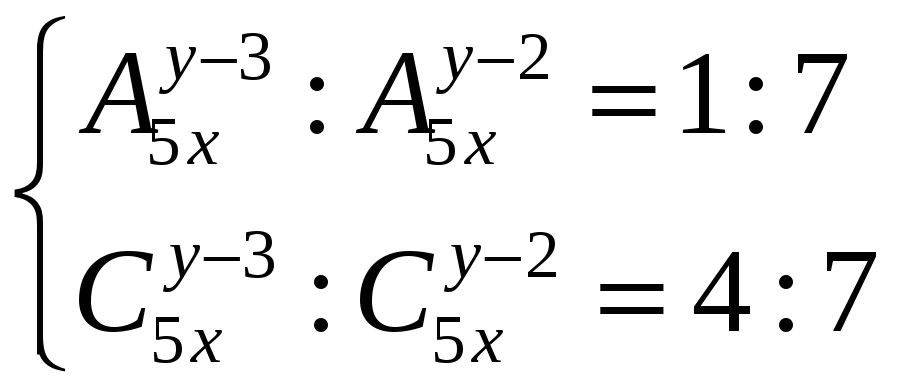

Розв'язання. Позначимо . Маємо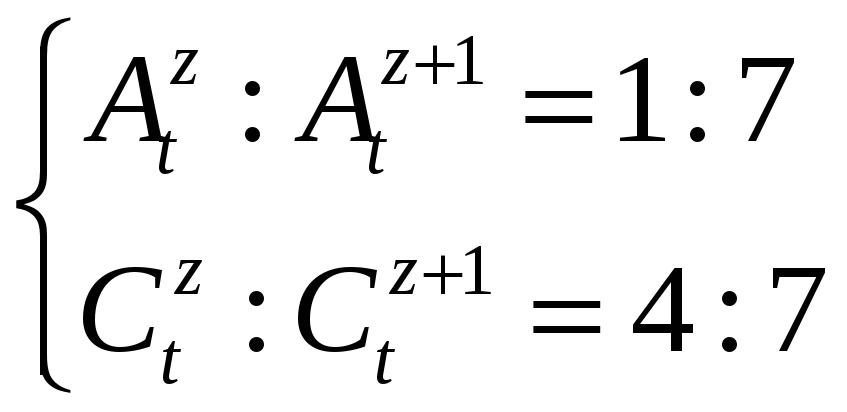

1) . 2) 3 системи маємо:

, .

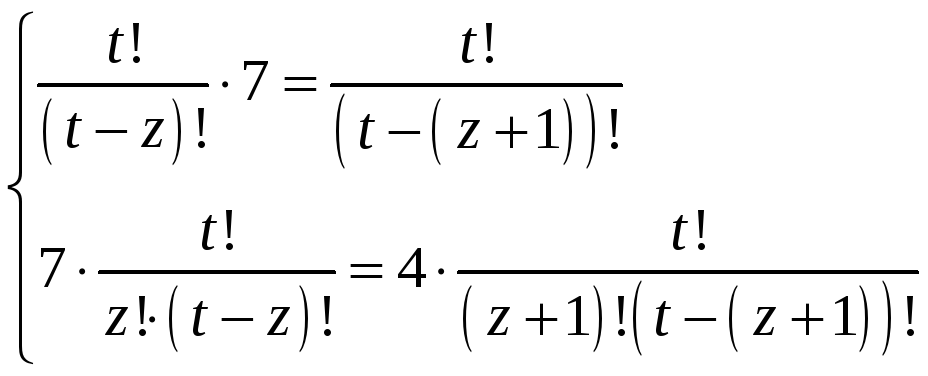Звідси z=3, а отже, t =10. Тому х = 2, у=6.

Домашнє завдання.