
- •2. Потенціальна та кінетична енергія.
- •3.Представлення коливань у вигляді вектора.
- •4. Вільні коливання.
- •5. Затухаючі коливання.
- •6.Змушені коливання. Резонанс.
- •7. Додавання коливань, биття, фігури Лісажу.
- •8.Струм через активний опір, ємність, індуктивність.
- •9. Векторні діаграми спадів напруг.
- •10.Вільні електричні коливання.(Незатухаючі)
- •11.Затухаючі електричні коливання
- •12.Змушені коливання, резонанс.
- •13. Резонанс напруги, резонанс струмів.
- •14. Магнітне поле.
- •15. Магнітний момент контуру зі струмом.
- •16.Вектор магнітної та напруженості магнітного поля.
- •17.Закон Біо-Савара-Лапласа.
- •18. Магнітна індукція нескінченно довгого провідника зі струмом , кругового провідника зі струмом.
- •19. Закон Ампера
- •21.Ефект Хола
- •22. Циркуляція вектора напруженості магнітного поля
- •23. Магнітна індукція соленоїда та тороїда
- •24. Потік вектора магнітної індукції
- •25. Робота переміщення провідника і контуру зі струмом у магнітному полі
- •26. Електрорушійна сила електромагнітної індукції.
- •27. Самоіндукція та взаємоіндукція.
- •28. Індуктивність та взаємоіндуктивність.
- •29. Індуктивність соленоїда.
- •30. Коефіцієнт взаємоіндуктивності двопровідної лінії.
- •32. Об’ємна густина енергії магнітного поля
- •33. Рівняння Максвела в інтегральному та диференціальному вигляді
- •Рівняння Максвела Струм зміщення
- •Система рівнянь Максвела
- •34. Шкала електромагнітних хвиль
- •Характеристики
- •37.Закони геометричної оптики.
- •38.Принципи Гюйгенса-Френеля.
- •Когерентність світла
- •40.Інтерференція.
- •41.Світловий вектор.
- •42.Вектор Умова-Пойтінга.
- •43.Смуги рівної товщини та нахилу.
- •44.Кільця Ньютона.
- •45.Дифракція на круглому отворі, одиничній щілині, дифракційній решітці, на просторовій дифракційній решітці.
- •46.Поляризація світла. Поляризоване світло.
- •47.Поляризація при відбитті та заломленні (закон Брюста).
- •48.Подвійне природне променезаломлення.
7. Додавання коливань, биття, фігури Лісажу.
Додамо гармонічні коливання однакового напрямуі однакової частоти:
 ,
,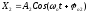 .
.
Для цього зобразимо гармонічне коливання графічно методом обертового вектора амплітуди або методом вектороної діаграми.
З точки 0,
вибрані на вісі Х, під кутами
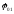 (початкова фаза першого коливання) і
(початкова фаза першого коливання) і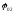 (початкова фаза другого коливання)
відкладаємо модуль амплітуд
(початкова фаза другого коливання)
відкладаємо модуль амплітуд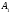 і
і (Рис.1).
(Рис.1).
При обертанні
векторів амплітуд навколо точки 0 з
кутовою швидкістю
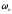 ,
проекції векторів будуть переміщуватись
по вісі Х в межах числових значень
амплітуд, змінюючись згідно з гармонічним
законом.
,
проекції векторів будуть переміщуватись
по вісі Х в межах числових значень
амплітуд, змінюючись згідно з гармонічним
законом.
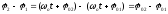
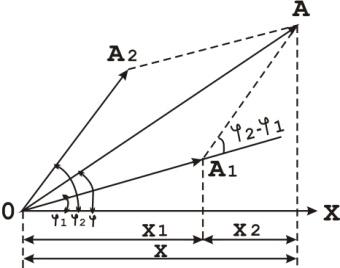
Очевидно, що рівняння результуючого коливання буде рівнянн гармонічного коливання тієї ж частоти і того ж напрямку.
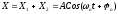
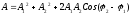 - теорема косинусів
- теорема косинусів
Відповідно малюнку
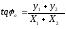 ;
;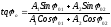 .
.
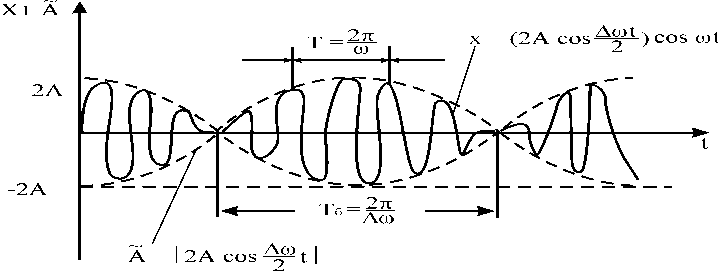
В результаті
додавання одержуємо коливання з
періодично змінюваного (пульсуючого)
амплітудою – биття (рис.2).
Нехай
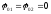 і
і ;
;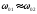 .
.
Тоді
 ;
;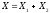 ;
;
Знайдемо рівняння результуючого коливання аналітичним методом:
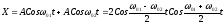
Результуюче коливання майже гармонічне з частотою і повільно гармонічне з частотою, що змінюється:
 .Пунктирна
лінія на рис.2 графічно це зображує.
Суцільна лінія – графік результуючого
коливання.
.Пунктирна
лінія на рис.2 графічно це зображує.
Суцільна лінія – графік результуючого
коливання.
Частота
змінювання модуля косинуса
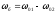 - частота биття, або
- частота биття, або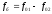 .
Період биття
.
Період биття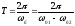 .
.
ДОДАВАННЯ ВЗАЄМНО ПЕРПЕНДИКУЛЯРНИХ КОЛИВАНЬ
Розглянемо випадок, коли коливальна система бере участь в 2-х взаємно перпендикулярних коливанняхз (промінь осцилографа при подачі гармонічної напруги на вертикальні і горизонтальні платівки).
Нехай
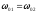 ;
; ;
;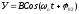 .
.
Рівняння траекторії результуючого коливання знаходиться шляхом виключення параметра t.
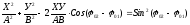
Розглянемо випадки:
1)
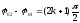 ,
тоді рівняння набуває вигляд
,
тоді рівняння набуває вигляд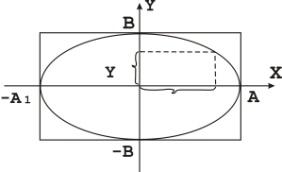
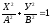 ,
якщо А=В, то
,
якщо А=В, то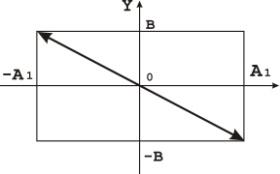
2)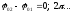
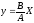
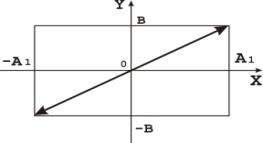
3)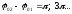
4)
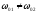 ,
то результуюче коливання відбувається
по складній траекторії, форма якої
залежить від різниці фаз і співвідношення
частот.
,
то результуюче коливання відбувається
по складній траекторії, форма якої
залежить від різниці фаз і співвідношення
частот.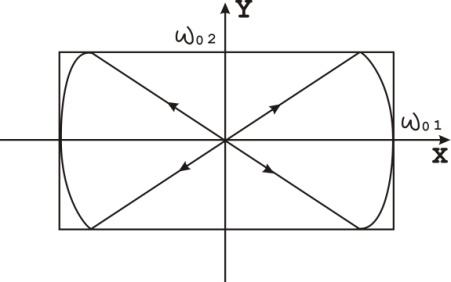
Якщо провести дотичні до траекторії, паралельні вісям, то відношення чисел дотиків обернено пропорційне частотам коливань, що додаються.
Методом фігур Ліссажувизначають невідому частоту.
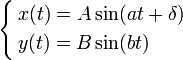 де
A,B
— амплітуди коливань,a,b
— частоти,δ
— зсув фаз.
де
A,B
— амплітуди коливань,a,b
— частоти,δ
— зсув фаз.
Вигляд
кривої сильно залежить від співвідношення
a/b.
Коли співвідношення дорівнює 1, фігура
Ліссажу має вигляд еліпсу, за певних
умов вона має вигляд кола (A
= B,
δ
= π/2радіан)
ілінії(δ
= 0). Інший приклад фігури Ліссажу —
парабола(a/b
= 2, δ
= π/2). Інші співвідношення продукують
більш складні фігури, які є замкненими
за умови a/b —
раціональне
число. Припускається, що візуальна
форма цих кривих є часто тривимірнимвузлом,
і насправді, проекції на площину багатьох
вузлів, включаючивузли
Ліссажу, є фігурами Ліссажу. Фігури
Ліссажу, деa = 1,
b = N
(N —
натуральне
число) і![]() єполіномами
Чебишевапершого роду степеняN.
єполіномами
Чебишевапершого роду степеняN.
8.Струм через активний опір, ємність, індуктивність.
Активний опір - частина повного опору електричного кола змінному струмові, яка поглинає електричну енергію і визначається вживаною потужністю P та струмом I в колі за формулою R= P/I2.
(далі за конспектом)
-через активний опір
Активний опір виникає в колі змінного струму і зумовлений безладним рухом вільних носіїв заряду.
U=I*R; a=F/m; v= a*t;
Umcosωt
ε 0cosωt
Алгебраїчна сума миттєвих ЕРС дорівнює миттєвим значенню спадів напруг.
I*R= ε0cosωt - Imcosωt; I= ε 0/R cosωt.
-через індуктивність
ε 0cosωt –L *di/dt=0; ε 0cosωt= L*di/dt; di= ε 0/L *cosωtdt;
i= ε 0/ωL *sinωt+ C; i= ε 0/ωL *cos(ωt-π/2); Im= ε 0/XL; U=i XL; XL=ωL.
-крізь ємність
Uc=q/C; i= dq/dt*i; q/C= ε 0cosωt; i= dq/dt= - ε 0ω*C*sinωt; i= ε 0ω*C*cos(ωt+ π/2); XC= 1/ ωC.
Струм, що тече в колі змінного струму (реальному, або RLC-контурі)
(за конспектом лекцій)
L*di/dt + q/C+ iR= ε0cosωt
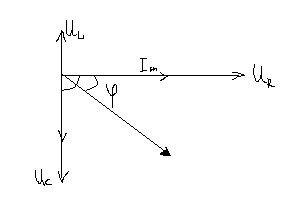
UL=ImXL=ImωL
UR=ImR
UC=ImXC=Im*1/ωC
UL-UC=Im(XL-XC)
