1. Комбинаторика. Правила суммы и произведения, формула включения и исключения, примеры применения. Сочетатания, перестановки, размещения, числа Стирлинга первого и второго рода, комбинаторный смысл этих чисел.

Совокупность подмножеств множестваX называется покрытием множества X если ,-блок покрытия.

Совокупность подмножеств множества X называется разбиением множества X, если

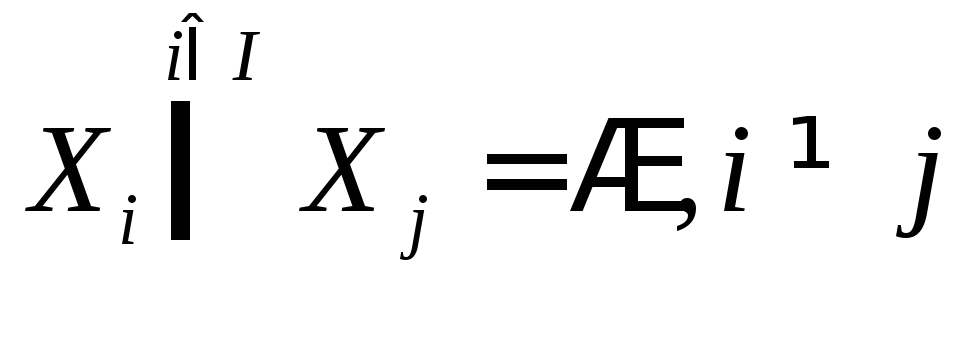1. 2. 3.

Правило суммы. Если разбиение множестваX, то

Пример 1. X- n-множество, Y- k-множество, . Обозначимчислоk-подмножеств Y в множестве X.

1. 2. 3.

C – семейство k-подмножеств, множества X.

Разделим C на два класса. В класс С₁ запишем те k-подмножества Y, которые содержат элемент a . В класс С₂ запишем все k-множества Y, которые не содержат а: .

Пример 2:

число способов выбора k элементов из X, среди которых нет двух соседних

,

Все выборки разделим на два класса:

1. Содержит

2. Не содержит

тогда

Правило произведения

Для любых конечных множеств справедливо равенство

Доказательство по индукции:

Шаг индукции k=2

Пример 1.

Размещение без повторений.

Перечислим упорядоченные последовательности длины n, где каждый элемент принимает m значений.

- количество размещений из m по n без повторений.

Пример 2.

Размещение с повторением. Если элементы из X будем считать различными шарами, а Y различными коробками, Сколько распределений существует n различных шаров по m различным коробкам.

Формулы включения-исключения

Характеристическая функция подмножества Y из множества X определяется:

Теорема: Пусть -совокупность подмножеств множестваX, . Тогда

J пробегает все непустые подмножества множества I

Доказательство: Будем опираться на 2 тождества

1.

2. Понятие характеристической функции

Доказательство: посчитаем вклад в правую и левую часть доказанной формулы.

Обозначим , тогда

Просуммируем формулу по , т.к. формула только для фиксированногоx.

Учитывая, что по свойству характеристической функции

получаем . Заметим, что формула принимает более простой вид, когда

I={1,2,…,n} :

В частности для n=2

Пример: Задача о беспорядках. Подстановка называется беспорядком, если у нее нет неподвижных точек, т.е.. Рассмотрим-группу подстановок, . Посчитаем количество беспорядков в ней. Обозначим -число беспорядков в ..

Заметим, что .

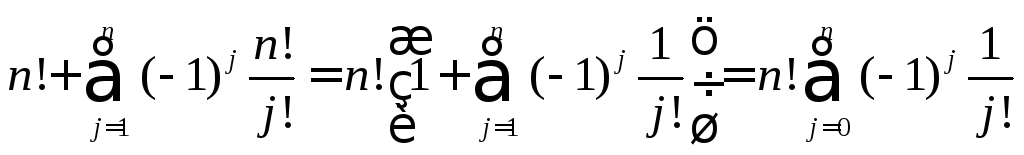
Перестановка без повторений – это размещение из m элементов по m без повторений.

Перестановка с повторением. Пусть имеются k предметы различных типов. Предметов первого типа -штук, второго -и т. д. . Если бы все предметы были различны, то число перестановок было бы n!. Рассмотрим перестановку вида (*). Элементы первого типа можно переставлять друг с другом способами, при этом общая перестановка не меняется. Аналогично для. Получим, что элементы перестановки (*) можно переставлять друг с другомспособами (т.к. перестановки элементов первого типа, второго и т.д. можно делать независимо друг от друга). Значит,число различных перестановок с повторениями будет

Сочетанием без повторений из n по k называется набор k элементов, выбранных из данных n элементов. Составим сначала все k сочетания из n элементов. Переставим входящие в каждое сочетание элементы всеми возможными способами, и получим, что из каждого k-сочетания можно получить k! штук k-размещений.

Сочетания с повторениями. Пара состоящая из множестваX, где и неотрицательной функциигде, называетсяk-мультимножеством, если .называется кратностью вхождения элементаx в k-мультимножество. Носителем мультимножестваназывается множество элементов, для которых.

-количество k-мультимножеств на n-множестве.

Пусть . Надо посчитать количество решений уравнения .

Каждому решению поставим в соответствие элемент из . Всегоk едениц и n-1 нулей. Задача свелась к нахождению количества способов расстановки n-1 нулей k+n-1 мест

Числа Стирлинга 2-го рода. Пусть |Y|=m. Разбиваем на k блоков. Рассмотрим неупорядоченное разбиение. Обозначим через S(m,k) число неупорядоченных разбиений множества Y на k блоков.

S(m, k ) – числа Стирлинга 2-го рода. Пусть S(0,0) = 1

Возьмем k>m.

,

Возьмем 2 < k < m и выведем рекуррентную формулу. Возьмем - фиксируем.полученное множество надо разбить наk блоков. S(m-1, k ) и помещаем элемент а в любой из этих блоков . Если элемент a образует блок , состоящий из одного элемента, тогда для остальных k-1 блоков .

Числа Стирлинга 1-го рода.

Задача о вычислении числа сюръекций. - число отображений n-различных шароф, по n –различным коробкам. F- множество всех распределений шаров по коробкам. .Выберем изF подмножества . Отнесем в те распределения для которыхi-ая коробка оказывается пустой. Возьмем -все распределения, содержащие пустые коробки, в точности не сюръективые выражения.= (*)

-попадают распределения с пустыми коробками с номерами из J, а остальные не пустые. , (*)=

-связь чисел Стирлинга первого и второго рода.

2.Графы

Пара (VG, EG) называется графом, если VG – непустое конечное множество элементов, называемых вершинами, EG – конечное семейство неупорядоченных пар элементов из VG (не обязательно различных), называемых ребрами.

Пара (VG, EG) называется простым графом, если VG - непустое конечное множество элементов, называемых вершинами, EG – конечное множество неупорядоченных пар различных элементов из VG, называемых ребрами (нет петель и кратных ребер).

Орграфом (ориентированным графом) называется пара (VD, ED), где VD – непустое конечное множество элементов, называемых вершинами, ED – конечное семейство упорядоченных пар элементов из VD, называемых дугами или ориентированными ребрами.

Виды графов.

1. Полный граф - это простой граф, в котором каждые две вершины смежные.

Количество ребер:

2. Предположим, что VG можем разбить на и, что,, так, что каждое ребро графа соединяет какую-нибудь вершину изс какой-нибудь вершиной из, тогда граф G называетсядвудольным.

3. Если каждая 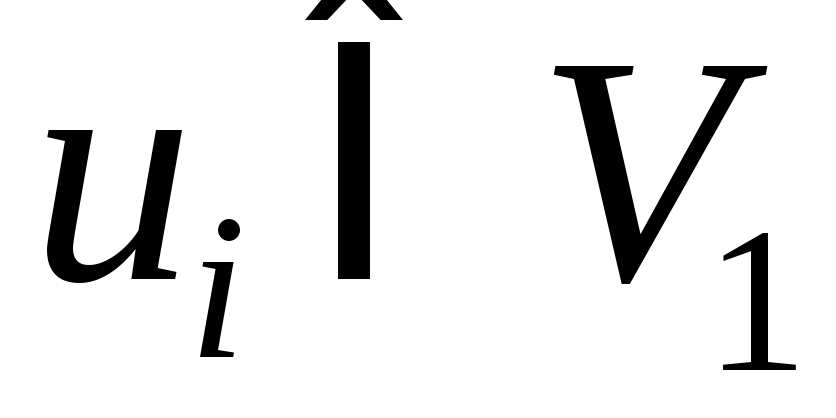соединена с каждойи граф является простым, то граф называетсяполным двудольным.( ).

4. Назовем граф связным, если его нельзя представить в виде объединения двух графов, и несвязным – в противном случае.

Объединением называется граф с множеством вершини множеством ребер.

5. В регулярном графе все вершины имеют одинаковую степень r (граф Петерсена).

Деревья, перечисление деревьев.

Лесом называется граф, не содержащий циклов. Связный лес называется деревом.

Теория перечисления графов занимается разработкой методов подсчета числа неизоморфных графов, обладающих теми или иными свойствами.

Два графа иназываютсяизоморфными, если существует взаимооднозначное соответствие между множествами их вершин, обладающее тем свойством, что число ребер, соединяющих каждые две вершины в графе , равно числу ребер, соединяющих соответствующие вершины в графе.Распределение меток в графе G c n вершинами определяется как взаимооднозначное соответствие между множеством вершин графа и множеством {1, 2, …, n}. Помеченным графом называется пара , где- граф,- распределение меток.

Теорема Кэли. Существует ровно различных помеченных деревьев свершинами.

Доказывается через следствие теоремы о биекции. Разделяющим множеством связного графа G называется такое множество его ребер, удаление которого приводит к несвязному графу. Назовем разрезом такое разделяющее множество, никакое собственное подмножество которого не является разделяющим. Если разрез состоит из одного ребра, то он называется мостом. Маршрутом графа G называется конечная последовательность ребер вида, где.

Маршрут называется цепью, если все его ребра различны, и простой цепью, если все его вершины различны (кроме, может быть, ).

Теорема о свойствах деревьев. Пусть T – граф, который имеет n вершин, тогда следующие утверждения эквивалентны: 1. T является деревом; 2. T не сожержит циклов и имеет n-1 ребро; 3. T связен и имеет n-1 ребро; 4. T связен и каждое его ребро является мостом; 5. Каждые 2 вершины графа T соединены ровно одной простой цепью; 6. T не содержит циклов, но, добавляя к нему любое новое ребро, мы получим ровно один цикл.

Доказательство: (12) Проведем индукцию по количеству ребер. Удаление любого ребра разбивает T на 2 графа, каждый из которых является деревом. Поэтому по индуктивному предположению число ребер в них меньше на 1, чем число вершин.

+ =- вершины

+ + 1 =- ребра

(23) Покажем, что граф связен. От противного.

Пусть граф T не связен, но каждая его компонента представляет связный граф без циклов. Из предыдущего доказательства: в каждой компоненте число вершин больше числа ребер на 1. Значит полное число вершин T больше полного числа ребер по крайней мере на 2. Это противоречит тому, что T имеет n-1 ребро.

(34) Видим, что удаление любого ребра приводит к графу с n вершинами и n-2 ребрами, который не может быть связен в силу слудующей теоремы.

Теорема. Если G можно представить , где- связные,, тогда- компонента связности, граф имеет k компонент связности. Пусть G имеет n вершин, m ребер и k компонент связности, G –простой, тогда выполняется неравенство:

Таким образом, получаем: .

Противоречие.

(45) Простая цепь – все вершины различны. Т.к. граф связен, то каждая пара его вершин соединена по крайней мере одной простой цепью (по определению связности).

Граф называется связным, если для любых двух его вершин существует простая цепь.

Если же данная пара вершин соединена двумя простыми цепями, то они замыкаются в цикл, а это противоречит тому, что каждое ребро в графе является мостом.

(56) От противного. Пусть T сожержит цикл, тогда каждые две вершины этого цикла соединены по крайней мере двумя простыми цепями.

Добавим к графу T ребро e, тогда получим цикл, поскольку инцедентные ребру e вершины уже соединены простой цепью. Мы получим только один цикл.

(61) От противного. Пусть T несвязен, тогда добавление любого ребра, соединяющего одну вершину одной компоненты связности с вершиной другой компоненты, не приводит к образованию цикла, что противоречит пункту 6.

Следствие.

Пусть G – лес с n вершинами и k компонентами связности, тогда G имеет n-k ребер.