Алгоритм нахождения двусвязных компонент неори­ентированных графов

Точками раздела называются вершины, при удалении которых граф перестает быть связным. Мосты — это ребра с аналогичным свойством.

Если в связном (состоящем из одной компоненты связности) графе нет точек сочленения, он – двусвязный.

Любой максимальный двусвязный подграф графа G называется компонентой двусвязности или блоком этого графа.

Две вершины s и t любого оррафа сильно связаны, если существует ориентированный путь из s в t и ориентированный путь из t в s.

Орграф называется сильно связным (strongly connected), если любые две его вершины сильно связаны. Сильно связными компонентами орграфа называются его максимально сильно связные подграфы.

Данный Алгоритм в своей основе имеет "Алгоритм обхода графа в глубину" (базовый) с внесением ряда изменений. Так как "базовый" алгоритм является достаточно известным, то описание его не приводится. Изменения состоят в том, что при попадании в уже обработанную вершину серого или черного цвета (то есть нахождение цикла) осуществляются следующие действия: все частично найденные двусвязные компоненты, которые пересекаются с найденным циклом хотя бы по одному ребру, объединяются со всеми ребрами цикла все вместе и это множество ребер обозначается как новая двусвязная компонента (старые двусвязные компоненты, принадлежащие этому множеству удаляются), или, если цикл ни с чем не пересекается, все его ребра обозначаются как принадлежащие к одной новой двусвязной компоненте.

По окончанию работы "базового" алгоритма все двусвязные компоненты найдены. Все ребра, не принадлежащие ни к одной из двусвязных компонент, помечаются как мосты, а вершины, которые они соединяют — как точки раздела (точками раздела становятся только те вершины, из которых выходят не меньше, чем два ребра).

Простейший алгоритм решения задачи о поиске сильно связных компонент в орграфе работает следующим образом:

1. При помощи транзитивного замыкания проверяем, достижима ли t из s, и s из t, для всех пар s и t.

2. Затем определяем такой неориентированный граф, в котором для каждой такой пары содержится ребро.

3. Поиск компонент связности такого неориентированного графа даст нам компоненты сильной связности нашего орграфа.

Очевидно основное время работы данного алгоритма приходится на реализацию транзитивного замыкания.

Также существует три алгоритма, решающих данную задачу за линейное время, то есть в V раз быстрее, чем приведенный выше алгоритм. Это алгоритмы Косарайю, Габова и Тарьяна.

Алгоритм Флойда: служит для поиска кратчайших расстояний между всеми парами вершин.

Пусть есть неориентированный взвешенный граф. Пусть длинна кратчайшего пути от i до j, проходящего по вершинам с индексом не более чем k. Изначально ребро . Эта величина и есть . Несложно заметить, что ответ задачи – это совокупность величин . Задача – найти .

Существует два варианта значения .

1. Кратчайший путь между i, j не проходит через вершину k, тогда =

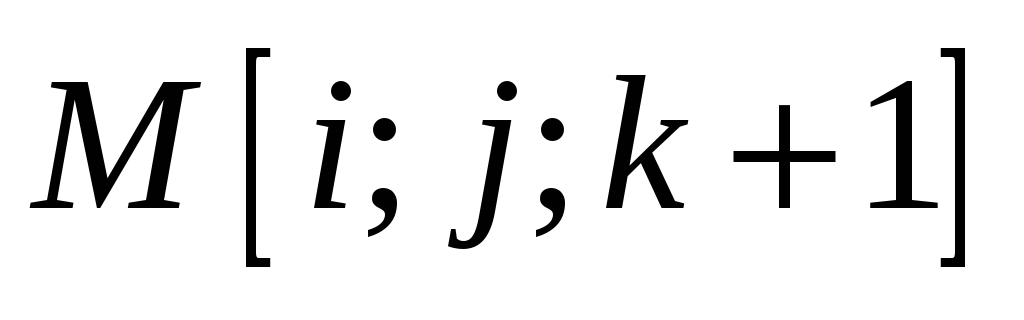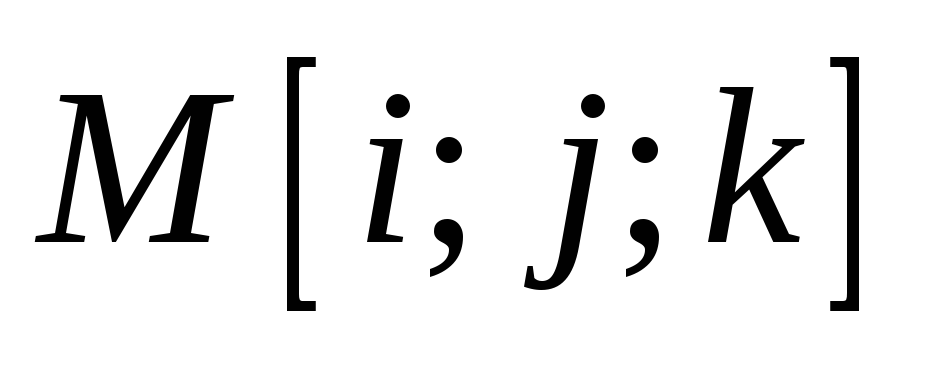
2. Существует более короткий путь между , проходящий через k, тогда он сначала идёт от i до k, а потом от k до j. В этом случае, очевидно, .

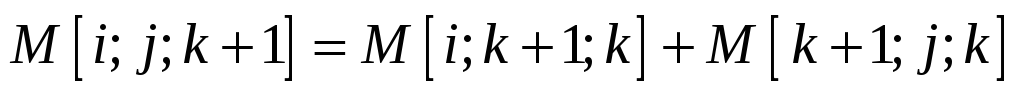Таким образом, для нахождения значения функции достаточно выбрать минимум из двух обозначенных значений. Очевидно, что имеет место соотношение:

Сам алгоритм:

for k = 1 to n

for i = 1 to n

for j = 1 to n

W[i][j] = min(W[i][j], W[i][k] + W[k][j])

Сложность алгоритма . Память использует только для хранения самого графа и некоторых вспомогательных переменных.

22. Алгоритмы внутренней сортировки.

• сортировки сравнениями (сортировка вставками, пирами­дальная сортировка, быстрая сортировка);

• карманная сортировка как пример распределяющей сортировки;

• оценки трудоемкости.