21. Алгоритмы на графах

граф — это совокупность объектов со связями между ними. Объекты представляются как вершины, или узлы графа, а связи — как дуги, или рёбра. Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и дополнительными данными о вершинах или рёбрах.

Алгоритм поиска в глубину

Поиск в глубину — один из методов обхода графа. Кратко суть алгоритма можно изложить так: для каждой непройденной вершины необходимо найти все непройденные смежные вершины и повторить поиск для них. Используется в качестве подпрограммы в алгоритмах поиска двусвязных компонент, односвязных компонент, топологической сортировки.

Пусть задан граф G = (V,E), где V — множество вершин графа, E — множество ребер графа.

Предположим, что в начальный момент времени все вершины графа окрашены в белый цвет. Выполним следующие действия:

1. Из множества всех белых вершин выберем любую вершину, обозначим её v1.

2. Выполняем для нее процедуру DFS(v1).

3. красим вершину v1 в черный цвет

4. Повторяем шаги 1-3 до тех пор, пока множество белых вершин не пусто.

Процедура DFS (параметр — вершина )

1. Перекрашиваем вершину u в серый цвет.

2. Для каждой вершины w, смежной с вершиной u, выполняем следующие два шага:

   1. Если вершина w окрашена в белый цвет, выполняем процедуру DFS(w).

   2. красим вершину w в черный цвет

3. В противном случае выводим информацию о том, что ребро обратное.

Время работы алгоритма зависит от представления графа. Если применена матрица смежности, временная сложность, если нематричное представление : рассматриваются все узлы и все ребра.

Алгоритмы нахождения компонент связности (поиск в ширину)

Поиск в ширину имеет отправной узел S, который обрабатывается первый. Поиск в ширину выполняется в следующем порядке: началу обхода s приписывается метка 0, смежным с ней вершинам — метка 1. Затем поочередно рассматривается окружение всех вершин с метками 1, и каждой из входящих в эти окружения вершин приписываем метку 2 и т. д.

В несвязанном графе процесс заканчивается после посещения всех узлов одной компоненты связанности. Поэтому поиск в ширину можно использовать для проверки связанности графа и выделения компонент связанности.

Для любой вершины графа заводится три характеристики:

1. Цвет вершины: - белый, черный, серый.

2. -предшественник на пути к корню поиска.

3. - глубина вершины .

Алгоритм BFS поиска в ширину (волновой алгоритм).

Пусть - вершина из которой производится поиск в ширину. фронт волны (очередь).

Сам алгоритм:

Поместить в вершину

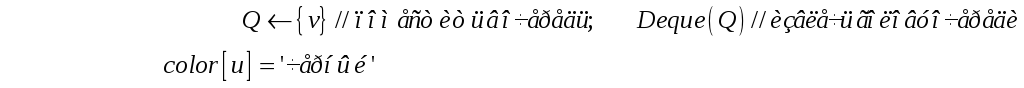
В результате получим глубину любой вершины и будем знать как построить кратчайший путь.

Теорема: Время работы алгоритма BFS есть , где Е – множество ребер, а - множество вершин.

Доказательство: Любое ребро в этом алгоритме анализируется только 1 раз. Если ребро между и проверилось, то это ребро «сереет», следовательно, дальше это ребро анализировать не будут.

Теорема: Сложность алгоритма BFS, реализованного с помощью матриц смежности есть .

Алгоритм Дейкстры

Дан простой взвешенный граф G(V,E) без петель и дуг отрицательного веса. Найти кратчайшее расстояние от некоторой вершины a графа G до всех остальных вершин этого графа.

Неформальное объяснение

Каждой вершине из V сопоставим метку — минимальное известное расстояние от этой вершины до a. Алгоритм работает пошагово — на каждом шаге он «посещает» одну вершину и пытается уменьшать метки. Работа алгоритма завершается, когда все вершины посещены.

Инициализация. Метка самой вершины a полагается равной 0, метки остальных вершин

бесконечности. Это отражает то, что расстояния от a до других вершин пока неизвестны. Все вершины графа помечаются как непосещенные.

Шаг алгоритма. Если все вершины посещены, алгоритм завершается. В противном случае из еще не посещенных вершин выбирается вершина u, имеющая минимальную метку. Мы рассматриваем всевозможные маршруты, в которых u является предпоследним пунктом. Вершины, соединенные с вершиной u ребрами, назовем соседями этой вершины. Для каждого соседа рассмотрим новую длину пути, равную сумме текущей метки u и длины ребра, соединяющего u с этим соседом. Если полученная длина меньше метки соседа, заменим метку этой длиной. Рассмотрев всех соседей, пометим вершину u как посещенную и повторим шаг.

Время работы алгоритма: n*ln(n) для очереди с приоритетом, n^2 - для простого перебора всех вершин

Очередь с приоритетом:

очередь у которой каждому элементу задается приоритет. при помещении элемента в очередь, он занимает место согласно приоритету

функции: pop - удалить элемент с наибольшим приоритетом

push - добавить элемент

top - получить элемент с наибольшим приоритетом

быстрый алгоритм:

Пусть дан граф, число вершин в котором есть N, и дана вершина S, из которой ищутся пути.

Помещаем в очередь пары (вершина,вес), где вес=0 если вершина=S и "бесконечность" в противном случае.

Алгоритм Дейкстры состоит из N итераций, каждая из которых будет пытаться улучшить значения D. В начале алгоритма все вершины помечаются как непосещённые. Если все вершины посещены, то алгоритм завершается. Иначе - из непосещённых вершин выбирается такая вершина X, которая имеет минимальное значение D[X] - это делается выталкиванием из очереди наибольшего значения до тех пор, пока вершина не окажется в списке непомеченных вершин. Далее, рассмотрим всевозможные рёбра, выходящие из X и входящие в непомеченную вершину, и попытаемся улучшить значение D вдоль этого ребра. Затем пометим вершину X как посещённую, вернем ее в очередь и выполним следующую итерацию.

Теперь мы сможем найти непосещённую вершину с минимальным значением D за O (log N). В то же время, стоимость релаксации (уменьшения D вдоль ребра) повышается до O (log N). Следовательно, итоговая сложность алгоритма составляет O (N log N + M log N) = O (M log N)