2. Атака вследствие отсутствия «семантической стойкости»

Используя дефект протоколов, Злоумышленник может извлекать частичную информацию о секретном сообщении, содержащемся в зашифрованном тексте, и организовывать атаки без взлома криптографического протокола по принципу «все или ничего».

30. Электронная подпись. Понятие эп. Эп Фиата – Шамира. Эп Эль-Гамаля;

Понятие ЭП: Цифровая подпись для сообщения является числом, зависящим от самого сообщения и от некоторого секретного, известного только подписывающему субъекту, ключа. При этом предполагается, что она должна быть легко проверяемой и что осуществить проверку подписи должен иметь возможность каждый (или заранее оговоренный круг лиц) без получения доступа к секретному ключу. При возникновении спорной ситуации, связанной с отказом подписывающего от факта подписи им некоторого сообщения либо с попыткой подделки подписи, третья сторона должна иметь возможность разрешить спор. Цифровая подпись позволяет решить следующие три задачи: 1. — осуществить аутентификацию источника сообщения, 2 — установить целостность сообщения, 3 — обеспечить невозможность отказа от факта подписи конкретного сообщения.

ЭП является до некоторой степени аналогом обычной подписи, чем и объясняется ее название. Для реализации ЭП необходимы 2 алгоритма – алгоритм вычисления ЭП и алгоритм ее проверки. Главные требования к алгоритму - невозможность подделки подписи без знания секретного ключа и достаточность открытого ключа. Надежность алгоритм определяется следующими тремя факторами: -1)сложность подделки подписи – нахождение подписи под документом без знания секретного ключа, 2) сложность создания подписанного сообщения- нахождение 1 сообщения с верной подписью, 3) сложность подмены сообщения – нахождение 2-х различных сообщений с 1 подписью, по парадоксу дня рождения эта задача в 2 раза проще 1-ой. Общая схема подписи на базе ассимитричного алгоритма с открытым ключом

- соответственно функции шифрования и дешифрования в ассиметричной системе шифрования. Условие Для преобразований (суперпозиция):

Тогда цифровая подпись сообщения будет определяться как (то есть «дешифрование» на закрытом ключе). Проверка подписи

В действительности для подписи берется обычно часть сообщений.

При этом при использовании затем шифрования к сообщению могут появиться дополнительные уязвимости в шифр-схеме, особенно для определенных пар ключей, не следует использовать одинаковые ключи для подписи и шифрования, и следует сначала подписывать, а затем шифровать сообщение, и не наоборот – иначе противник заведомо получит некоторый кусочек открытого текста, примененный для вычисления подписи и соотвтствующий ему шифр-текст. Такой алгоритм не устойчив к 2) виду атак, так как при проверке подписи мы получаем исходное сообщение(его часть). Можно для подписи дополнительно использовать бесключевую ХЭШ-функцию - по значению подписи сообщение не восстановишь

Можно, наоборот, внести избыточнсть в сообщение.

Цифровая подпись Фиата-Шамира. -основана на сложности факторизации больших чисел и извлечении квадратного корня в кольце вычетов

Пусть h - некоторая хеш-функция, преобразующая исходное сообщение в битовую строку длины m, р и q – различные простые числа, n = pq . В качестве секретного ключа каждый абонент должен сгенерировать m различных случайных чисел . Открытый ключ - набор чисел, где . Алгоритм вычисления цифровой подписи для сообщения М состоит в выполнении следующих действий:

1. Выбрать случайное число . 2. . 3.

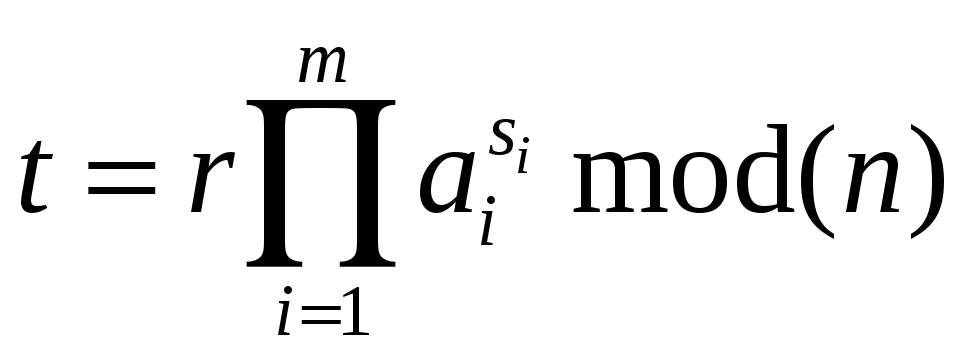4. . 5. подпись M

Алгоритм проверки подписи состоит в выполнении сле­дующих действий:

1. . 2.

3. Подпись принимается, если s = s'.

Корректность: покажем

Достоинствами описанной схемы являются возможность выработки цифровых подписей для нескольких различных сообщений с использованием одного секретного ключа, а также сравнительная простота алгоритмов вычисления и проверки подписи. Например, для схемы цифровой подписи, основанной на алгоритме RSA, соответствующие алгоритмы требуют выполнения значительно большего числа умножений. Попытка компрометации этой схемы сталкивается с необходимостью решения сложной задачи нахождения квадратных корней по модулю n.

Недостатком схемы является большая длина ключа, которая определяется числом m. Если двоичная запись числа n содержит l знаков, то длина секретного ключа составляет ml бит, а открытого ключа - (m+1)l бит. При этом необходимо учитывать, что для обеспечения достаточной стойкости данной схемы цифровой подписи числа l и m должны иметь в своей двоичной записи несколько сотен бит.

Цифровая подпись Эль-Гамаля. - основана на сложности вычисления логарифма в конечном поле. Пусть р - простое число, - примитивный элемент поля Z_p. - случайное число, которое является секретным ключом, , набор (р, , ) - открытый ключом.

Подпись для сообщения М вычисляется с помощью следующего алгоритма:

1. Случайное целое число - секретное(пояснение ниже)

2.

3.

4. Подписью для сообщения M положить пару (,).

Подпись принимается, если выполняется сравнение.

Корректность

Основным достоинством такой схемы цифровой подписи является возможность выработки цифровых подписей для большого числа сообщений с использованием одного секретного ключа.

Зам 1: Число r должно каждый раз выбираться заново, повторное использование этих чисел не допускается, при этом алгоритм генерации этих чисел должен быть надежным.. Зная число r и значение подписи, легко вычислить секретный ключ a:

- подпись скомпрометирована

Зам 2: реально при вычислении подписи на шаге 3 алгоритма целесообразнее использовать свертку h(M) в степени, а не само сообщение М. Это защищает схему подписи от возможности подбора сообщений с известным значением подписи.

Схема цифровой подписи Эль-Гамаля послужила образцом для построения большого семейства во многом сходных по своим свойствам схем подписи. В их основе лежит проверка сравнения вида ^A^B  ^C (mod p), в котором тройка (А, B, C) совпадает с одной из перестановок чисел ±х, ± и ± при некотором выборе знаков. Например, исходная схема Эль-Гамаля получается при А = х, В = - и С =  . На базе схем подписи из этого семейства построены и стандарты цифровой подписи США и России. Так, в американском стандарте DSS (Digital Signature Standard) используются значения А=х, В = и С =, а в российском стандарте - значения А= -х, В = и С = .

Еще одним достоинством схемы Эль-Гамаля является возможность уменьшения длины подписи путем замены пары чисел (, ) на пару чисел ( mod q,  mod q), где q является некоторым простым делителем числа р-1. При этом проверочное равенство по модулю р следует заменить на модифицированное равенство по модулю q: (^A^B mod p) mod q = ^C (q). Именно так сделано в американском стандарте цифровой подписи DSS.