15. Простые числа специального вида (числа Мерсена и числа Ферма)

Числа n вида , где . Если m делится на простое , т.е. делится на, т.е. является составным. Поэтому простым числоn может быть лишь при .

ОПР: Числа называются числами Ферма.

Проверка простоты чисел Ферма:

Теорема: Число приявляется простым тогда и только тогда, когда

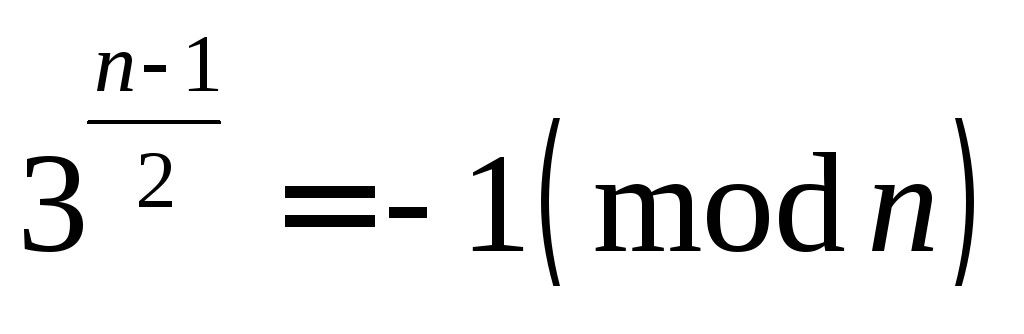
Док-во: (достаточность)

Поскольку - степень 2, порядокравен. Следовательно,содержит не менееn-1 элемента, и поэтому все ненулевые элементы обратимы, т.е.n – простое число.

Док-во: (необходимость)

Заметим, что . Поэтому. По квадратичному закону взаимности; по критерию Эйлера.

ОПР: Пусть p- простое число, и - так же простое. Тогданазывается числом Мерсенна.

Проверка простоты чисел Мерсенна.

Теорема: Пусть q – простое число, . Рассмотрим последовательностьопределяемую соотношениями. Числоn простое тогда и только тогда, когда