11. Символы Лежандра и Якоби, квадратичный закон взаимности Гаусса.

Число a называется вычетом степени n по модулю m, если сравнение имеет решение. В противном случаеa называется квадратичным невычетом степени n по модулю m. Пусть p- простое нечетное, (a,p)=1.

Определение: Символ Лежандра

Часто полагают , если.

Свойства:

1. (Критерий Эйлера)

2. (из определения).

3. (частный случай свойства 1).

4. Если .()

5. .

Доказательство:

6.

Доказательство:

.

Квадратичный закон взаимности Гаусса.

Полагая , рассмотрим сравнения

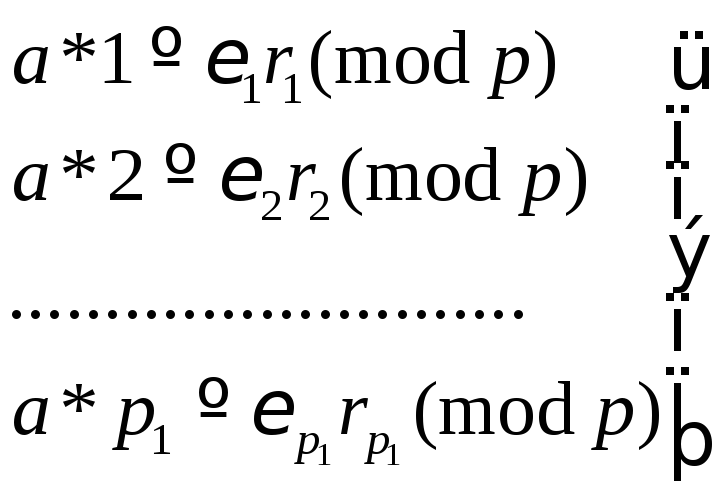, где -абсолютно наименьший вычет числа,-его модуль, так что.

Лемма 1: Символ Лежандра. .

Числа образуют приведенную систему вычетов по модулюp.

Их абсолютно наименьшие вычеты будут . Положительные из последних, т.е.должны совпадать с. Перемножая теперь сравнения и сокращая наполучим

. (по критерию Эйлера-есть символ Лежандра)

Получаем .

Лемма 2:

. Это число будет четным или нечетным в зависимости от того, меньше или большечислот.е. в зависимости от того, будет ли наименьший неотрицательный вычет числаменьше или больше, т.е. будет ли или . Отсюда очевидно .

Лемма 3: Символ Лежандра.

Лемма 4: (7-ое свойство Символа Лежандра)

Пусть a – нечетное => a+p (нечет+нечет) – четное

Получаем

Положим а=1, тогда

Лемма 5:

, ,

Из этих двух равенств следует что,

Теорема: Квадратичный закон взаимности Гаусса

Пусть p и q – различные простые нечетные =>

Д-во: Пусть , . Рассмотрим множество

. Заметим, что равенство py=qx невозможно, т.к. если py=qx, то qx делится на p, p|qx, но x<p => p|q, что не возможно по усл. p и q простые.

Разобьем мн-во S на 2 подмн-ва S₁ и S_2. S1∩S2=0

. Обозначим s₁=|S₁|, s₂=|S_s| => p₁q₁=|S|=s₁+s₂

Посчитаем мощность мн-ва S₁ .

При каждом данном y, x может быть , т.к., аи так для любогоy S₁ содержит пар(qx,py), значит значитаналогично,, ,

, ,

Символ Якоби. Пусть P – нечетное, P>1 P=p₁p₂…p_n, где p_i – простые числа, могут быть равные между собой. Пусть (a,P)=1 – символ Якоби..

Свойства Символа Якоби:

1)

Док-во:

Так как , то, следовательно

2) .

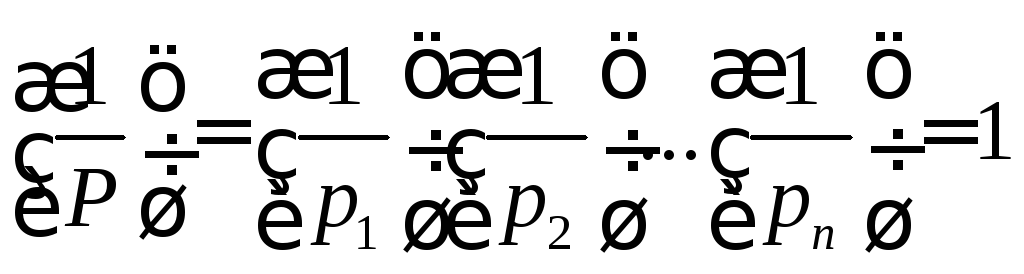
3)

Док-во:

по св-ву символа Лежандра

Утв: по mod 2

,

Док-но.

4)

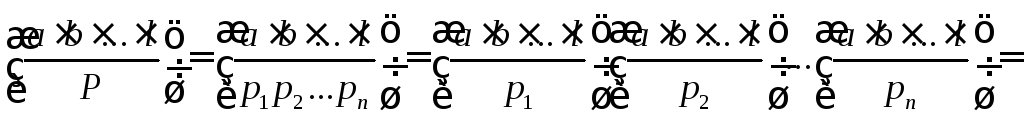
5)

Док-во:

Но, ввиду чего получаем

6) (P,Q)=1 P,Q – нечетн.

P=p₁p₂…p_n, Q=q₁q₂…q_n, p_i,q_j – простые

12. Все случаи существования первообразных корней.

Пусть (a, m)=1, , существуют положительные такие, что . Наименьшее из таких называется показателем, которому принадлежит a по модулю m.

(a, m)=1, число a принадлежит показателю по модулю m, если такое число a существует, оно называется первообразным корнем по модулю m.

Теорема 1. p – нечетное простое число. Первообразные корни по модулю p существуют.

Теорема 2. p – нечетное простое число, g – первообразный корень по модулю p, тогда

неотрицательное , где (U, p)=1. При каждом таком t число g+pt будет первообразным корнем по модулю , .

Теорема 3. p – нечетное простое число, . Первообразные корни по модулю существуют.

Теорема 4. (ГЛАВНАЯ) Все случаи существования первообразных корней.

Если первообразные корни по модулю m существуют, то , p – нечетное простое.

Доказательство: Пусть - нечетное. Посчитаем функцию Эйлера:

. Пусть к – наименьшее общее кратное чисел , тогда (назовем утверждение 1).

Заметим, что для любого а, взаимнопростого с m выполняется: . И действительно:делится на. Далее, дляпо той же причине. Другими словами по свойству сравнений мы показали что (назовем утверждение 2).

Другими словами мы показали, что показатель любого числа по модулю m является делителем числа k. Таким образом, если первообразные корни существуют по модулю m, то делитk. С учетом утверждения 1 получим: . Итак: пусть, докажем теперь чтоn=1 или n=2. Посчитаем: - четное при. Посчитаем для:- четное при.

Обозначим через - наивысшую степень числа 2, которая делитсоответственно. Наивысшая степень 2, на которую делитсяэтоНаивысшая степень 2 на которую делитсяэто. Так как. Т.е. 1. еслиn=0, то m=. 2. еслитоn=1, . Покажем что не существует первообразных корней по модулюкогда. Имеет место любое нечетноеa, удовлетворяющее:

- по определению первообразного корня, если - наш показатель.. Рассмотримвспомогательное утверждение: . Пусть а – нечетное. Т.е. а=2x+1. База индукции

.

. И т.д.

Предположение индукции: Пусть

Шаг индукции:

Теперь полагаем , таким образом утверждение доказано по индукции. Вспомним что, т.е. по модулювсе нечетные числа имеют показатель, значит, показатель не может быть. Следовательно, первообразных корней по модулюприне существует.Что и требовалось доказать.