
- •9. Вычеты. Полная система вычетов. Полная система наименьших неотрицательных вычетов. Полная система абсолютно наименьших вычетов. Приведенная система вычетов. Сравнения, свойства сравнений.
- •10. Теорема Эйлера и теорема Ферма.
- •11. Символы Лежандра и Якоби, квадратичный закон взаимности Гаусса.
- •12. Все случаи существования первообразных корней.
- •13. Критерий Вильсона
- •14. Вероятностные тесты определения простоты числа (на основе теоремы Ферма, Соловея-Штрассена, Рабина –Миллера).
- •15. Простые числа специального вида (числа Мерсена и числа Ферма)
9. Вычеты. Полная система вычетов. Полная система наименьших неотрицательных вычетов. Полная система абсолютно наименьших вычетов. Приведенная система вычетов. Сравнения, свойства сравнений.
Опр. Рассмотрим множество целых чисел Z где: m – модуль, m – классов. Возьмем из каждого класса по одному числу. Получим m – чисел по одному из каждого класса. Эти m чисел - это полная система вычетов. Каждое число из класса называется вычетом.
Полная система наименьших неотрицательных вычетов (ПСННВ) по модулю m это система чисел вида: 1,2,3 … m-1. (или ПСПНВ – полная система положительных наименьших вычетов)Полная система абсолютно наименьших вычетов (ПСАНВ):
если m=2k+1, то ПСАНВ это: -k,….., -2,-1,0,1,2,…,k.
если m=2k то ПСАНВ любая из двух: -(k-1),…,-1,0,1,..,k или -k,..,-1,0,1,..,k-1.
Пример: m=10: ПСПНВ: 0,1,2,3,4,5,6,7,8,9. ПСАНВ: -4,-3,-2,-1,0,1,2,3,4,5 или -5,-4,-3,-2,-1,0,1,2,3,4
Лемма 1: Любые m чисел попарно несравнимых друг с другом образуют полную систему вычетов. Д-во: Если m чисел попарно несравнимы друг с другом, то они принадлежат разным классам, а поскольку чисел m и классов m, то каждому классу принадлежит по одному из этих чисел, которые вместе образуют полную систему вычетов. ЧТД
Лемма 2: Пусть
(a,m)=1,
![]() .
Если x
пробегает полную систему вычетов по
модулю m,
то ax+b
тоже пробегает полную систему вычетов
по модулю m.
.
Если x
пробегает полную систему вычетов по
модулю m,
то ax+b
тоже пробегает полную систему вычетов
по модулю m.
Д-во: Пусть
![]() тогда
тогда
![]() достаточно показать что числа во втором
множестве попарно несравнимы по модулю
m.
От противного: пусть числа сравнимы, то
есть
достаточно показать что числа во втором
множестве попарно несравнимы по модулю
m.
От противного: пусть числа сравнимы, то
есть
![]() по свойствам сравнения
по свойствам сравнения
![]()
![]() что невозможно, так как
что невозможно, так как
![]() принадлежат разным классам, следовательно
они несравнимы. ЧТД
принадлежат разным классам, следовательно
они несравнимы. ЧТД
Опр. По свойству сравнения все вычеты одного класса чисел по модулю m имеют с m один о тот же НОД, и с каждого класса чисел, для которых этот НОД=1 берем по одному числу, получаем систему чисел, которая называется приведенная система вычетов по модулю m.
Число чисел в
приведенной системе вычетов равно в
точности
![]() -
(функция Эйлера – количество чисел ряда
1,2, .. m
взаимно простых с m.
-
(функция Эйлера – количество чисел ряда
1,2, .. m
взаимно простых с m.
 ,
где
,
где
![]() )
)
Лемма 1:
Любые
![]() чисел попарно несравнимых по модулю m
и взаимно простых с m
образуют приведенную систему вычетов
по модулю m.
чисел попарно несравнимых по модулю m
и взаимно простых с m
образуют приведенную систему вычетов
по модулю m.
Д-во:
Классов чисел, вычеты которых имеет с
m
НОД=1 в точности
![]() .
Имеем
.
Имеем
![]() чисел, чей НОД с m
равен 1 и при этом они принадлежат разным
классам, то есть они образуют приведенную
систему вычетов по модулю m.
ЧТД
чисел, чей НОД с m
равен 1 и при этом они принадлежат разным
классам, то есть они образуют приведенную
систему вычетов по модулю m.
ЧТД
Лемма 2: Пусть (a,m)=1 Если x пробегает полную систему вычетов по модулю m, то ax тоже пробегает полную систему вычетов по модулю m.
Д-во: Пусть
![]() тогда
тогда
![]() достаточно показать что числа во втором
множестве попарно несравнимы по модулю
m.
От противного: пусть числа сравнимы, то
есть
достаточно показать что числа во втором
множестве попарно несравнимы по модулю
m.
От противного: пусть числа сравнимы, то
есть
![]() по свойствам сравнения
по свойствам сравнения
![]() что невозможно, так как
что невозможно, так как
![]() принадлежат разным классам, следовательно
они несравнимы. ЧТД
принадлежат разным классам, следовательно
они несравнимы. ЧТД
Сравнения,
свойства сравнений![]() разобьем на классы
Опр.
Возьмем m>0,
разобьем на классы
Опр.
Возьмем m>0,
![]() ,
m
– модуль. Целые числа a
и b назовем сравнимыми
по модулю
m, если они имеют равные остатки от
деление на m.
,
m
– модуль. Целые числа a
и b назовем сравнимыми
по модулю
m, если они имеют равные остатки от
деление на m. ![]() Пример: m=5.
Пример: m=5.![]() ,
,![]() ,
,![]()
[0] [1] …. [m-1]
Эти классы не пересекаются, их
объединение дает
![]()
Утверждения: следующие 3 условия равносильны:
1.
![]()
2. a-b делится на m
3. a=b+mt,t – целое.
Д-во: 1->2 Из![]() следует:a=mq+r;
b=mq1+r
=> a-b=m(q-q1),
2->3 Из a-b делится на m следует a-b=tm =>
a=b+tm
3->1 Из Обратно так же (из a=b+mt
следует что
следует:a=mq+r;
b=mq1+r
=> a-b=m(q-q1),
2->3 Из a-b делится на m следует a-b=tm =>
a=b+tm
3->1 Из Обратно так же (из a=b+mt
следует что
![]() )
)
Свойства:
Сравнение по модулю m является отношением эквивалентности на множестве
 ,
т.е.
,
т.е. (рефлексивность)
(рефлексивность) =>
=>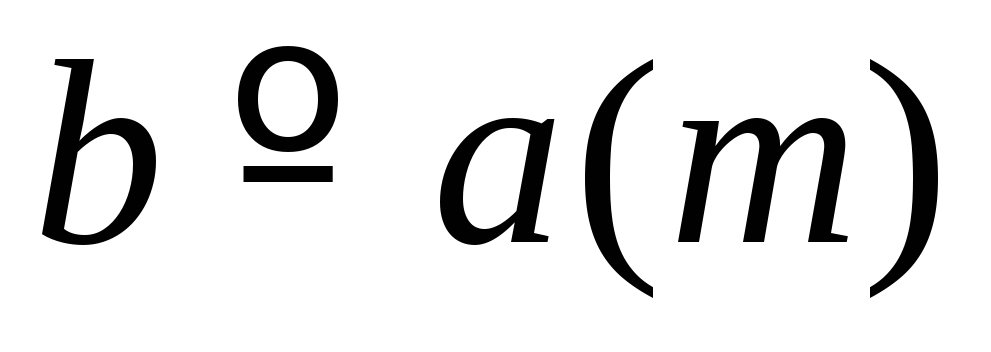 (симметричность)
(симметричность)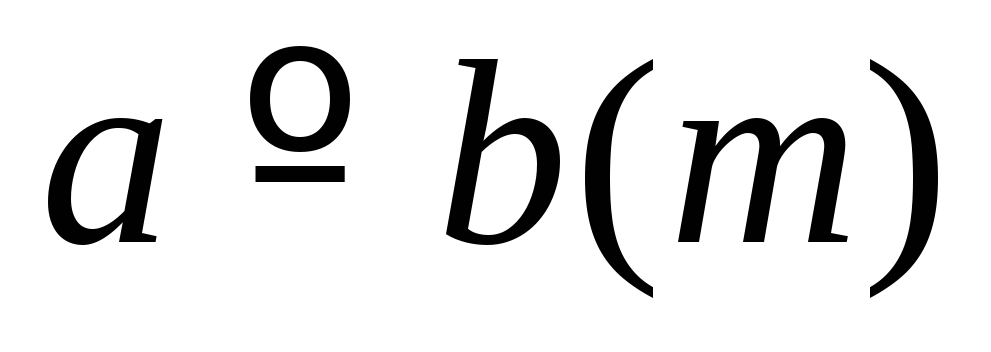 ,
, =>
=> (транзитивность)
(доказывается из a=b+mt)
(транзитивность)
(доказывается из a=b+mt)
Сравнение по модулю m является конгруэнтностью на множестве
 ,
т.е. отношением эквивалентности с двумя
дополнительными условиями
,
т.е. отношением эквивалентности с двумя
дополнительными условиями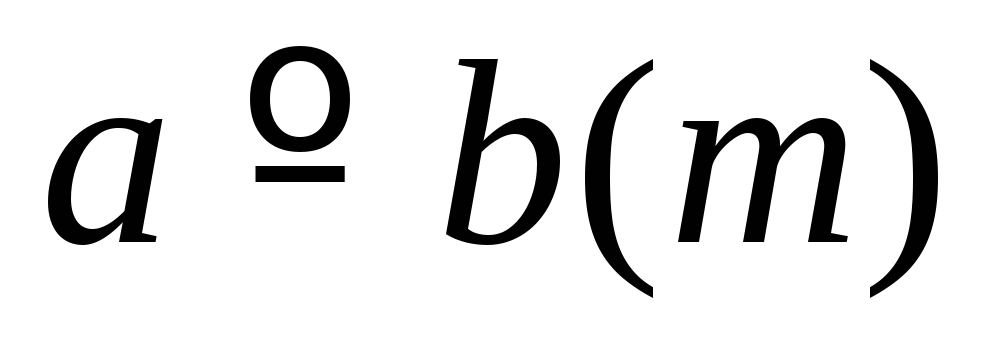 ,
,
 =>
=>
 ,
,
 =>
=>
Обе части сравнения можно поделить на их общий делитель, если этот общий делитель взаимно прост с модулем
Д-во:
![]() ,
,![]() =>
=>
![]() =>
=>![]() =>
=>![]() =>
=>
![]()
Обе части сравнения можно умножить на одно и тоже число
Д-во:
![]() =>
=>
![]() =>
=>![]() =>
=>![]() =>
=>
![]()
Обе части сравнения и модуль можно умножить на одно и тоже число
Д-во: Из
![]() следует
следует![]()
Обе части сравнения и модуль можно поделить на их общий делитель
Д-во: Пусть
![]() Имеем
Имеем![]()
Если сравнение имеет место по модулю m, то оно имеет место по модулю – делителю числа m.
Д-во: Из
![]() следует,
что разность а-b
должна делиться на m,
поэтому она должна делиться и на любой
делитель d
числа m
следует,
что разность а-b
должна делиться на m,
поэтому она должна делиться и на любой
делитель d
числа m
Если сравнение имеет место по нескольким модулям, то оно имеет место по модулю равному НОК этих модулей.
 =>
=>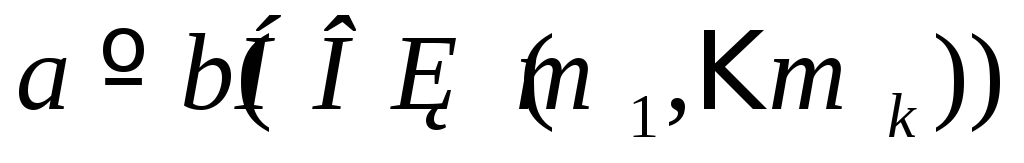
Д-во: Из
![]() следует,
что разностьa-b
делится на все модули
следует,
что разностьa-b
делится на все модули
![]() Поэтому
разность должна делиться и на НОКm
этих модулей
Поэтому
разность должна делиться и на НОКm
этих модулей
Если одна часть сравнения и модуль делятся на некоторое число, то и другая часть сравнения делится на это же число
Д-во: Пусть
![]() ,
,![]() ,
,![]() =>
=>
![]() =>
=>
![]() =>
=>![]() =>
=>![]() =>
=>![]()
Обе части сравнения имеют с модулем один и тот же НОД.
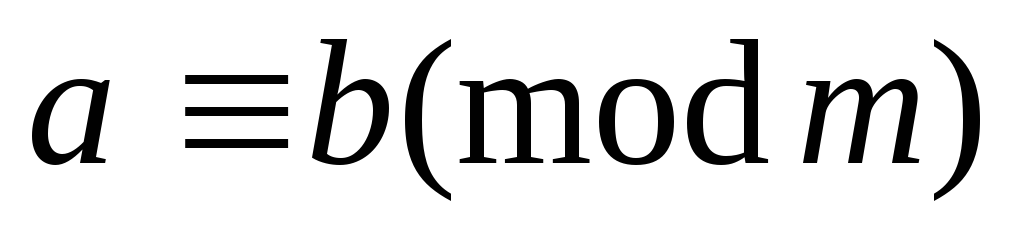 =>
=>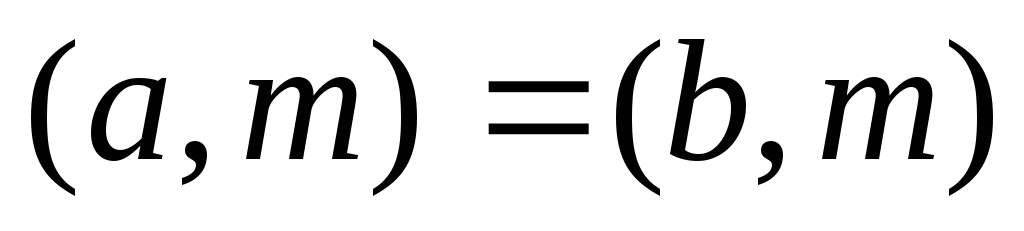 (по свойству НОД)
(по свойству НОД)
