16. Энтропия и информация

• виды информации: собственная информация, условная информация, взаимная информация;

• энтропия вероятностной схемы и ее свойства;

• условная энтропия и ее свойства.

• взаимная информация и ее свойства.

• дискретный источник без памяти.

а) виды информации: собственная информация, условная информация, взаимная информация; г) взаимная информация и ее свойства;

Определение

Распределение вероятностей — это закон, описывающий область значений случайной величины и вероятности их принятия.

Определение

Конечное множество U вместе с заданным на нём распределением вероятностей называется дискретным ансамблем сообщений и обозначается символом .

Определение

Пусть идва конечных множества. Символомбудем обозначатьдекартово произведение множеств X и Y, элементами которого являются упорядоченные пары . ЕслиX=Y, то произведение будем обозначать через .

Определение

Пусть на множестве задано совместное распределение вероятностей, которое каждой паре, сопоставляет вероятность. Ясно, что соотношенияизадают распределение вероятностейи на множествах X и Y. Таким образом при задании ансамбля фактически задаются ещё два ансамбляи. Ансамблиибудем называть совместно задаваемыми с ансамблем.

Определение

Пусть исовместно заданы с ансамблем. Зафиксируем некоторое элементарное сообщениеи рассмотрим условное распределениенаX. Для каждого сообщения в ансамблеопределенасобственная информация:, которая называетсяусловной собственной информацией элемента сообщения при фиксированном сообщении.

Определение

Количеством информации о сообщении , содержащейся в сообщении, называется величина. Так как, то. Поэтому количество информации о сообщениии сообщенииравно количеству информации о сообщениив сообщении, то есть.

На этом основании называютколичеством взаимной информации между сообщениями x и y или просто взаимной информацией между сообщениями x и y.

Взаимная информация между сообщениями обладает следующими свойствами:

1. Если сообщения x и y независимы, то есть , то сообщениеy не даёт никакой информации о сообщении x. В этом случае .

2. Если сообщение y содержит в себе сообщение x, то есть , тогда

Определение

Математическое ожидание случайной величины на ансамбленазываетсясредним количеством взаимной информации или просто средней взаимной информацией между ансамблями и

б) энтропия вероятностной схемы и ее свойства;

Определение

Среднее количество информации, содержащееся в отдельном сообщении, называется энтропией источника

Свойства энтропии

1. Энтропия любого дискретного источника неотрицательна. Равенство возможно лишь в том случае, когда источник генерирует одно единственное сообщение с вероятностью равной единице.

2. Пусть N объём алфавита дискретного источника. Тогда , причём равенство имеет место лишь в том случае, когда все сообщения равновероятны.

Так как прии, то

т.е.

3. Свойство аддитивности: энтропия нескольких совместно заданных статических дискретных источников сообщений равна сумме энтропий исходных источников.

Энтропия совместного источника равна

в) условная энтропия и ее свойства;

Определение

Математическое ожидание случайной величины, определённой на ансамбленазывается условной энтропией ансамбляX относительно ансамбля Y.

Свойства условной энтропии.

1. , равенство имеет местокогда ансамблиX и Y статистически независимы

Равенство возможно когда, то есть когдаx и y независимы для всех и

2. Имеет место соотношение

называемое свойством аддитивности энтропии. В самом деле с помощью равенства , находим. Аналогично, пользуясь соотношениемможно получить.

3. Теорема о не возрастании информации при отображении.

Теорема

Пусть задан ансамбль и на нём определено отображение ,. Это отображение определяет ансамбль, где. Пустьиэнтропии ансамблейX и Y, тогда .

Знак равенства имеет место когда отображениеобратимо, т.е.является взамно однозначным отображениемX в Y.

Доказательство.

Совместное распределение на произведении множествзадаётся соотношением, гдееслии, если. Тогда либо, либо. Поэтому

Из аддитивности и неотрицательности энтропии получим, что

.

Энтропия сохранится когда . Поэтому для всехимеем, значитдля всехпри каждом. Тогда для каждогосуществует единственный, такой что. Последнее равенство выполняется если , т.е. отображениеобратимо.

В случае будем говорить, что ансамбльY однозначно определяет ансамбль X.

4. Пусть вводит три совместно заданных ансамбляX,Y,Z и пусть

есть условная собственная информация при фиксированной паре сообщений y,z, где

.

Число

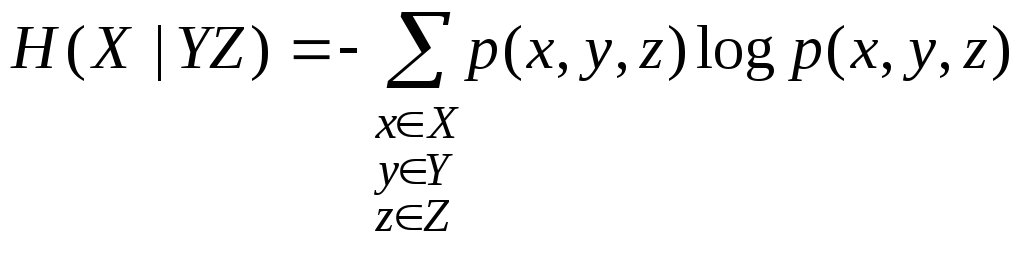
Называется условной энтропией ансамбля X относительно пары ансамблей Y,Z.

Имеет место следующее неравенство.

Равенство выполняется когдадля всех, то есть когда при данном сообщенииy сообщения x и z статистически независимы.

Это неравенство обобщается на случай n совместно заданных ансамблей. Рассмотрим ансамбль . Тогда для любыхs и m, , выполняется неравенство .

5. Свойство аддитивности допускает обобщение. Если n совместно заданных ансамблей, тогда

.

Из свойства 4 следует, что и равенство возможно когда ансамблистатистически независимы, то есть, где. Если источникисовпадают с источникоми статистически независимы, то.

д) дискретный источник без памяти.

Определение : Дискретным источником без памяти(ДИБП) называется источник сообщений такой что для любых и любой последовательности , имеет место равенство

2. Коды источника. Скорость кодирования, скорость создания информации; теоремы Шеннона об источниках; префиксные коды, неравенство Крафта; коды Шеннона – Фено, оптимальные коды Хаффмана.

Обозначим через A некоторое множество, состоящее из D, D>1, элементов: . Назовем егоалфавитом кода источника. Элементы алфавита A будем называть кодовыми символами. Последовательности кодовых символов будем называть кодовыми словами, а любое семейство кодовых слов – кодом на алфавитом A. Код называется равномерным, если все слова имеют одинаковую длину. Количество различных слов неравномерно года с max длиной кодовых слов m равно D(D^m-1)/(D-1).

Кодированием сообщений ансамбля X посредством кода называется отображение (необязательно взаимно однозначное) множества сообщений во множество кодовых слов.

P.S. Конечное множество X вместе с заданным на нем распределением вероятностей p(x), называется дискретным ансамблем сообщений и обозн.{X, p(x)}.

Предположим, что при кодировании последовательность сообщений на выходе источника разбивается на блоки длиной n и каждому блоку кодер сопоставляет кодовое слово длиной m. Число кодовых слов обозначим символом M. Будем считать, что длина кодовых слов m определяется числом кодовых слов M: m – наименьшее целое, удовлетворяющее неравенству M ≤ D^m. Описанный метод кодирования называется равномерным кодированием.

Число - называетсяскоростью равномерного кодирования источника посредством кода с M кодовыми словами при разбиении последовательности сообщений на блоки длины n. Скорость двоичного кодирования измеряется в двоичных символах на сообщение источника (бит/символ).

Скоростью создания информации дискретным источником при равномерном кодировании называется наименьшее число H такое, что для любого R > H и любого сколь угодно малого положительного числа найдетсяn (длина кодируемых сообщений) и равномерный код со скоростью кодирования R, для которого вероятность ошибки декодирования не превосходит .

P.S. определения скорости кодирования и создания информации для неравномерного кода после теорем Шеннона.

Теоремы Шеннона об источниках (вроде бы они)

Теорема (Прямая теорема): Пусть R>H(X), тогда для любого положительного существует код со скоростьюR, который кодирует дискретный источник без памяти с вероятностью ошибки, не превышающей .

Доказательство: Зададимся положительным и выберемтакое, что. Найдется такоеN, что для любого n>N . Так как, можем выбратьв качестве множества однозначно кодируемых последовательностей. Тогда вероятность ошибки декодирования не будет превышать. Тем самым, построен код с2^nR кодовыми словами и с вероятностью ошибки, не превышающей .

Теорема доказана.

Теорема (Обратная теорема): Пусть R<H(X), тогда существует, зависящее от R положительное такое, что каждого кода, кодирующего дискретный источник без памяти со скоростьюR, вероятность ошибки P_e не менее, чем . Кроме того, для любой последовательности кодов со скоростьюR

(1), где P_en – вероятность ошибки для кода, кодирующего отрезки сообщений длины n.

Доказательство: Докажем сначала (1). Пусть и,n=1,… - последовательность высоковероятных множеств и пусть |X|=L. Рассмотрим последовательность кодов со скоростью R. Через T_n обозначим множество однозначно кодируемых сообщений. Тогда . Поэтому

Из теоремы о высоковероятных множествах следует, что . Рассмотрим вероятность. Для всякогоимеем. Число элементов в множествене превосходит. Поэтомуприn→0.

Докажем первое утверждение теоремы. Заметим, что при R<H(X) и поэтому множествоT_n не пусто для каждого n. Так как основной характеристикой неравномерного кодирования является количество символов, затрачиваемых при кодировании одного элементарного сообщения. Обозначим через m_i длину слова, кодирующего сообщение . Пустьp(x_i) – вероятность этого сообщения. Тогда есть средняя длина кодовых слов, кодирующих ансамбль{X, p(x)}. Предположим, что неравномерными кодами кодируются сообщения длины n, то есть кодируется ансамбль сообщений . Так какp(x)≠0 для каждого , то для каждогоn найдется , такое что.

С другой стороны, существует такое N, что для всех n>N выполняется неравенство . Положим, тогда для любогоn и любого T_n .

Теорема доказана.

Число называетсясредней скоростью неравномерного кодирования посредством двоичного кода при разбиении последовательности сообщений на блоки длины n.

Коды, в которых ни одно слово не является началом другого называют префиксными. Префиксные коды являются кодами со свойством однозначного декодирования.

Скорость создания информации источником при неравномерном кодировании называется наименьшее число H такое, что для любого R>H найдется n (длина кодируемых сообщений) и неравномерный код со средней скоростью кодирования R, который допускает однозначное декодирование.

Есть теорема, доказывающая, что скорость кодирования при неравномерном кодировании, как и при равномерном, равна энтропии источника на элементарное сообщение.

Т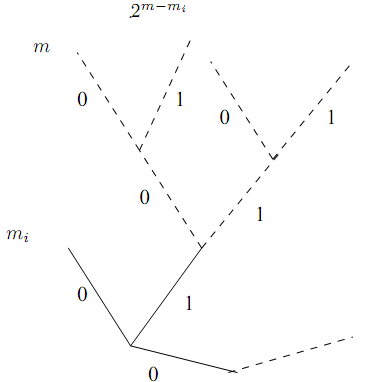еорема (Неравенство Крафта): Для того, чтобы существовал двоичный префиксный код с длинами кодовых слов m₁, m₂, …,m_M необходимо и достаточно, чтобы выполнялось неравенство (1).

Доказательство:

Необходимость. Заметим, что максимальное число узлов на каждом ярусе j равно D ^j. Пусть m = max {m₁,…,m_M}. Рассмотрим концевой узел порядка m_i. Этот узел отстоит от яруса m на m-m_i ребер и, следовательно, исключается из яруса возможных узлов. Так как количество узлов, исключаемых из ярусаm всеми концевыми узлами порядков m₁,…,m_M, не может превосходить максимального количества узлов на этом ярусе , то . После деления обеих частей неравенства наD^m получаем (1).

Достаточность. При выполнении (1) дерево с концевыми узлами порядков m₁,…,m_M может быть построено. Предположим, что среди этого набора порядков числа s встречается ровно раз,s = 1,…,m. Тогда . Перепишем это неравенство следующим образом. Тогда(2). Применим метод мат.индукции. Дерево, содержащееконцевых узлов порядка 1 может быть построено. Из (1) следует, что, то есть. Так как максимально возможное количество концевых узлов порядка 1 равно 2 и, то дерево сконцевыми узлами порядка 1 может быть построено.

Предположим, что дерево с концевыми узлами порядкаs, s = 1,…,i-1, может быть построено. Докажем, что к этому дереву можно добавить еще концевых узлов порядкаi. Если верно предположение индукции, то из яруса порядка i исключается возможных концевых узлов, каждый узел из ярусаs исключается из яруса i (2^i-s возможных узлов). Так как максимальное количество возможных концевых узлов на этом уровне равно 2ⁱ, то есть количество свободных узлов на ярусе i. Из (2) следует, что количество узлов на ярусеi, которые должны быть добавлены, не превосходит количество свободных узлов. Следовательно, к дереву с концевыми узлами порядкаs, s = 1,…,i-1, могут быть добавлены концевых узлов порядкаi.

Теорема доказана.

Теорема: для любого неравномерного кода со свойствами однозначного декодирования верно неравенство

Примером неравномерного кода является код Шеннона - Фено. При кодировании по методу Шеннона - Фено алфавит, расположенный в порядке убывания вероятностей появления символов, разбивается на две группы таким образом, чтобы сумма вероятностей появления символов в каждой группе была приблизительно одинаковой. Каждая группа в свою очередь также разбивается на две по такому же принципу. Операция продолжается до тех пор, пока в каждой группе не останется по одному символу. Каждый символ обозначается двоичным числом, последовательные цифры которого (нули и единицы) показывают, в какую группу попал данный символ при очередном разбиении. В коде Шеннона–Фено часто встречающиеся буквы кодируются относительно короткими двоичными символами, а редкие – длинными.

Кодирование Шеннона—Фено является достаточно старым методом сжатия, и на сегодняшний день оно не представляет особого практического интереса. В большинстве случаев, длина последовательности, сжатой по данному методу, равна длине сжатой последовательности с использованием кодирования Хаффмана. Но на некоторых последовательностях могут сформироваться неоптимальные коды Шеннона—Фено, поэтому более эффективным считается сжатие методом Хаффмана.

Оптимальным кодом называется код, средняя длина кодовых слов равна минимально возможной. В простейшем случае, когда вероятность элементарных сообщений источника {X, p(x)}, X={x₁,…,x_M} являются целыми отрицательными степенями двойки ,i=1,…,M, любой двоичный код со свойствами однозначного декодирования является оптимальным, так как средняя длина кодовых слов равна (по безымяннойth выше). В таком коде сообщению x_i ставиться в соответствие слово длины m_i. Всякое дерево с набором концевых вершин порядков m₁,…,m_M и указанным правилом дает оптимальный код. Методом построения такого дерева является, например, код Шеннона-Фено.

Лемма (1) (без доказательства): В оптимальном коде слово, соответствующее наименее вероятному сообщению, имеет наибольшую длину.

Лемма (2) (без доказательства): В оптимальном двоичном префиксном коде два наименее вероятных сообщения кодируются словами одинаковой длины, которые, можно считать, различаются только в последнем знаке, одно из них оканчивается нулем, а другое – единицей.

Лемма (1) (без доказательства): Если оптимален однозначно декодируемый префиксный код для ансамбля X’, то оптимален, полученный из него префиксный код для ансамбля X.

Задача построения оптимального префиксного кода сводиться к задаче построения оптимального префиксного кода для ансамбля, содержащего на одно сообщение меньше. В этом ансамбле снова можно выделить два наименее вероятных сообщения и, объединяя их, получить новый ансамбль, содержащий уже на два сообщения меньше, чем исходный. Продолжая эту процедуру можно дойти до ансамбля, содержащего два сообщения, оптимальным кодом для которого являются 0 и 1. Описанный метод построения префиксного кода называется методом Хаффмена.

Классический алгоритм Хаффмана на входе получает таблицу частот встречаемости символов в сообщении. Далее на основании этой таблицы строится дерево кодирования Хаффмана.

1. Символы входного алфавита образуют список свободных узлов. Каждый лист имеет вес, который может быть равен либо вероятности, либо количеству вхождений символа в сжимаемое сообщение.

2. Выбираются два свободных узла дерева с наименьшими весами.

3. Создается их родитель с весом, равным их суммарному весу.

4. Родитель добавляется в список свободных узлов, а двое его детей удаляются из этого списка.

5. Одной дуге, выходящей из родителя, ставится в соответствие бит 1, другой — бит 0.

6. Шаги, начиная со второго, повторяются до тех пор, пока в списке свободных узлов не останется только один свободный узел. Он и будет считаться корнем дерева