Лабы по физике, Механика / lab18

ЛАБОРАТОРНАЯ РАБОТА № 18

ИЗМЕРЕНИЕ МОМЕНТА ИНЕРЦИИ КОЛЕСА

ЦЕЛЬ РАБОТЫ: проверка основного закона динамики для вращающихся тел и измерение момента инерции колеса.

ОБОРУДОВАНИЕ: установка, секундомер, штангенциркуль.

КРАТКАЯ ТЕОРИЯ

Вращательное движение характеризуется угловым перемещением точек тела φ, угловой скоростью ω = dφ/dt и угловым ускорением ε = dω/dt. При вращательном движении все точки тела имеют одинаковую угловую скорость и одинаковое угловое ускорение. Перемещение любой точки вращательного тела за промежуток времени Δt можно измерить дугой окружности ΔS, пройденной точкой за это время. Выражая угловое перемещение точки тела Δφ в радианах и обозначая через r радиус окружности, описанной данной точкой вокруг оси вращения, получим

Δ S = r  Δ φ.

При очень малом угловом перемещении тела dφ можно заменить весьма малую дугу, пройденную точкой, прямолинейным отрезком dS. Тогда

d S = r  d φ. (1)

Это равенство устанавливает связь между линейными и угловыми перемещениями точек вращающегося тела. Линейная и угловая скорости, линейное и угловое ускорения точек вращающегося тела связаны друг с другом соотношениями

V = ω r , α = ε r. (2)

При поступательном движении перемещение, скорость и ускорение являются векторными величинами (полярные векторы). Во вращательном движении угловое перемещение, угловая скорость и угловое ускорение однозначно определяются лишь тогда, когда известно положение оси вращения в пространстве и указанно направление поворота вокруг этой оси. Поэтому эти величины определяются тоже как векторы, направление которых связывается с направлением вращения, или обхода (аксиальные векторы). Соотношение (2) в векторной форме имеет вид:

V = [ω, r] , α = [ε,r]. (3)

Для определения вектора угловой скорости удобно пользоваться правилом буравчика. Вектор угловой скорости ω направлен по оси вращения в сторону поступательного движения острия буравчика, когда рукоятку его вращают в направлении вращения тела. Направление вектора углового перемещения совпадает с направлением вектора угловой скорости. Когда направление оси вращения тела остается неизменным, вектор углового ускорения ε при увеличении угловой скорости совпадает с направлением вектора ω, а при уменьшении ее направлен в противоположную сторону.

Изменение скорости поступательного движения твердого тела определяется вторым законом Ньютона: α = F/m, т.е. ускорение зависит как от величины действующей силы, так и от массы тела. Изменение скорости вращательного движения твердого тела, имеющего закрепленную ось вращения, обусловливается тангенциальной составляющей силы, действующей на тело. Эта составляющая расположена в плоскости, перпендикулярной к оси вращения. При этом угловое ускорение зависит не только от величины этой составляющей силы, но и от кратчайшего расстояния l от оси вращения до линии, вдоль которой она действует, т.е. так называемого плеча силы. Поэтому в динамике вращательного движения вместо силы рассматривают момент силы (или тангенциальной ее составляющей) относительно оси вращения или центра вращения.

Момент силы M относительно вращения определяется вектором, модуль которого численно равен произведение силы на плечо:

M = F  l

Направление вектора момента силы определяется по правилу правого буравчика. Если вместо плеча силы l воспользоваться радиусом-вектором r точки приложения силы относительно сои вращения, то

M = [r, F]. (4)

Угловое ускорение вращающегося тела зависит не только от массы вращающегося тела, но и от распределения массы относительно оси вращения. Поэтому в динамике вращательного движения вместо массы рассматривают момент инерции тела относительно оси вращения.

Твердое тело можно представить как систему материальных точек. Скалярную величину Δm_ir_i² , равную произведению массы материальной точки на квадрат расстояния ее от оси вращения, называют моментом инерции материальной точки относительно этой оси. Сумму моментов инерции всех точек тела относительно оси вращения называют моментом инерции тела относительно этой же оси:

.

Как масса — мера инертности при поступательном движении, так и момент инерции — мера инертности при вращательном движении. При вращении тела вокруг различных осей моменты инерции различны. Величина момента инерции тела относительно какой-либо оси определяется пространственным распределением элементарных масс тела — т.е. геометрией масс. Аналитическое вычисление величины момента инерции производится путем интегрирования выражения:

,

где  — плотность вещества в элементе объема dV, находящегося на расстоянии r от оси вращения.

При сложной форме поверхности, ограничивающей тело, и неравномерном распределении плотности аналитический подсчет величины момента инерции может быть достаточно сложной задачей. Экспериментальное же определение момента инерции осуществимо легко.

В настоящей работе момент инерции велосипедного колеса измеряется двумя различными способами.

УПРАЖНЕНИЕ 1

Определение момента инерции методом вращения

Зависимость углового ускорения вращающегося тела от момента действующей на тело силы и момента инерции тела относительно оси, вокруг которой происходит вращение, определяется основным законом динамики вращательного движения

Μ = Ι  (при Ι = const) (5)

Зная M и , можно определить Ι.

Схема установки показана на рис.1.

Велосипедное колесо (1) может вращаться с малым трением вокруг горизонтальной оси ОО.

Колесо имеет соосные к ним шкивы (2), на которые наматывается нить с прикрепленным к ней грузом (3). Под действием силы тяжести груз будет опускаться, приводя колесо во вращение. Если намотать нить на шкивы, поднять груз на высоту h, затем позволить ему падать то на колесо начнет действовать вращающий момент

M = [r, T],

где r — радиус шкивы, на котором намотана нить;

T — сила натяжения нити (сила, приложенная по касательной к шкиву).

Рис. 1. Схема установки.

1 — колесо.

2 — шкивы.

3 — груз.

4 — шкала.

Чтобы найти натяжение нити Т, рассмотрим движение груза массой m. Согласно основному закону динамики поступательного движения ускорение системы определяется результирующей силой, действующей на груз mα = mg – Т.

При этом пренебрегаем силой трения. Окончательно для силы натяжения получим

T = m (g – α).

Тогда момент силы, действующий на колесо

M = m (g – α) r. (6)

Угловое ускорение колеса, приобретаемое под действием этого момента, может быть выражено через тангенциальное ускорение точек окружности шкива (или линейное ускорение груза):

. (7)

Ускорение груза можно найти, считая движение груза равноускоренным, если известно время t , в течении которого груз проходит расстояние h, т.к. . По известным М и ε можно определить Ι , используя основной закон динамики вращательного движения.

Попробуем учесть силы трения. Они создают момент сил трения М_тр. Тогда основной закон динамики для вращательного движения можно записать так

Μ – Μ_тр = Ι ε, (8)

или

. (8’)

Обозначим ε = y, M = x, 1/y = b, -M_тр/ I = a.

Тогда уравнение (8’) примет вид y = b x + α. По методу наименьших квадратов можно найти величины а и b и, следовательно М_тр и I, а также их погрешности.

Учет сил трения может быть произведен и другим способом. При опускании груза m с высоты h (на полную длину нити) его потенциальная энергия переходит в кинетическую энергию W_кин системы и работу против сил трения

m g h = W_кин + φ М_тр, (9)

где φ — полный угол поворота колеса.

После того, как груз опустится на полную длину нити h, колесо будет продолжать вращаться и нить начнет наматываться на шкив (обязательно на тот, с которого происходило сматывание нити!). В результате груз поднимается на максимальную высоту h₁ < h. Очевидно, W_кин = mgh₁ + φ₁ M_тр , где φ₁ — полный угол поворота колеса при подъеме груза. Учитывая, что h = r φ, а h₁ = r φ₁, получим

(10)

Эта формула позволяет вычислить величину момента силы трения.

План выполнения упражнения разработайте самостоятельно. Данные заносите в таблицу, форму которых тоже определите самостоятельно. Вычертите график ε = f(М). Оцените ошибки измерений.

УПРАЖНЕНИЕ 2

Определение момента инерции методом колебаний.

Велосипедное колесо может вращаться с малым трением вокруг горизонтальной оси О. Закрепляя на ободе колеса груз (2), имеющий массу m, получаем физический маятник, который может колебаться вокруг положения равновесия, отклоняясь влево и вправо от вертикали, проходящей через ось колеса. Угол отклонения может быть определен по угломерной шкале (3).

Рис.2. Схема установки

1 — колесо.

2 — груз.

3 — транспортир.

Пренебрегая моментом силы трения, напишем уравнение движения колеса вместе с грузом m

, (11)

где I_x — момент инерции колеса,

I — момент инерции груза относительно оси колеса, m — масса груза, L — расстояние между центром масс груза и осью колеса, φ — угол отклонения колеса от положения равновесия, — угловое ускорение колеса.

Если sinφ  φ (малые углы отклонения), то можно написать

. (12)

Зная, что процесс движения периодический, примем закон движения в виде

φ = φ₀ sin ωt , (13),

где ω = 2π /Τ — циклическая частота, Т — период колебаний колеса, φ₀ — амплитуда колебаний.

Из уравнения (13), дифференцируя его по времени, получаем

= -ω²φ (14)

Сопоставляя уравнения 12) и (14), нахоодим

. (15)

Учитывая, что размеры груза много меньше радиуса колеса, можем считать груз материальной точкой и положить

. (16)

Тогда из уравнений (15) и (16) получаем

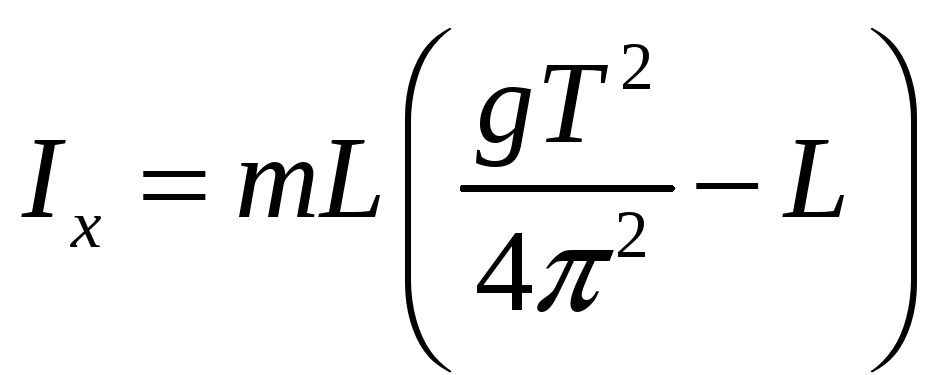(17)

Вычисление момента инерции колеса по этой формуле требует измерение массы груза, периода колебаний и расстояния от оси вращения до центра масс груза.

План выполнения упражнения разработайте самостоятельно. Данные измерений занесите в таблицу, форму которой тоже определите самостоятельно. Оцените погрешность измерений. Сопоставьте момент инерции колеса, определенный по формуле (17) с моментом инерции колеса, полученным в предыдущем упражнении.

Контрольные вопросы

1. Что понимают под угловой скоростью ω и угловым ускорением

2. ε ? Как направлены эти векторы?

3. Какая величина называется моментом силы, относительно некоторой точки? Что такое плечо силы?

4. Какая величина называется моментом инерции тела относительно оси?

5. Сколько моментов инерции может иметь данное тело? Что произойдет с моментом инерции, если ось переместить параллельно самой себе, удаляясь от тела?

6. Откуда следует, что момент инерции тела равен сумме моментов инерции отдельных его частей?

7. Сформулируйте теорему Гюйгенса-Штейнера.

8. Как можно определить момент инерции тела неправильной геометрической формы?

ЛИТЕРАТУРА

1. Сивухин Д.В. Общий курс физики: В 5 т. Т.1. Механика.—М.: Наука,1979.— §§ 30, 32, 33, 35, 36, 41.

2. Стрелков С.П. Механика.—М.:Наука, 1965.— §§ 50, 51, 52, 54, 59.

3. Савельев И.В. Курс общей физики. В 3 т. Т.1. — М.:Наука, 1977.— §§ 5, 38, 49, 196.

4. Хайкин С.Э. Физические основы механики. — М.:Наука, 1971.— §§ 13, 14, 67, 68, 69, 70, 71, 89, 90.