ЛАБОРАТОРНАЯ РАБОТА №7

Упражнение 1

ИЗУЧЕНИЕ ЗАКОНА СОХРАНЕНИЯ ИМПУЛЬСА.

ЦЕЛЬ РАБОТЫ: 1) проверить закон сохранения импульса при упругом ударе.

2) определить: а) время соударения шаров;

б) коэффициент восстановления;

в) энергию остаточной деформации;

г) среднюю силу упругого удара.

ОБОРУДОВАНИЕ: специальная установка, частотомер-хронометр, выпрямитель.

Краткая теория

Специальная установка представляет собой два маятника равной длины с равными массами в виде шаров. Конструкция установки изображена на рис.1.

Рис.1 Схема установки

Треугольное основание 6 установлено на трех винтах 8, которые фиксируются стопорными гайками 9. На основании крепится труба 1, в верхней части которой находятся направляющие 12. По этим направляющим перемещаются муфты 13, к которым на бифилярных подвесах 10 прикреплены шары 2. На муфтах имеются регулировочные гайки 11, при вращении которых изменяются высоты подвеса шаров. Направляющая левого шара перемещается в горизонтальном направлении при помощи рукоятки 5 или от руки. Передвигая эту направляющую влево или вправо, можно менять межцентровое расстояние шаров. Для удержания шаров в крайнем положении установлены электромагниты 3, крепящиеся на винтах к шкале 4. Шкала 4 перемещается в горизонтальном направлении, ее положение фиксируется стопорным винтом 7. Передвигая шкалу влево или вправо, можно установить нулевое деление шкалы против указателя, который укреплен снизу каждого шара.

Проявление закона сохранения импульса удобно наблюдать при взаимодействии двух тел, например, при ударе шаров. При этом в зависимости от материала и вида удара шаров закон сохранения механической энергии может и не выполняться, в то же время закон сохранения импульса выполняется при любом ударе.

Удар — совокупность явлений, возникающих при кратковременном приложении к телу внешних сил или при взаимодействии двух движущихся относительно друг друга тел в момент их соприкосновения. При этом происходит значительное изменение скоростей тел за очень короткий промежуток времени.

На практике удар протекает в течение тысячных или даже миллионных долей секунды. Процесс удара можно разделить на две фазы. Сжатие — центры тяжестей тел сближаются. Эта фаза заканчивается в момент наибольшего сближения, когда деформации тел становятся наибольшими, а скорость сближения обращается в нуль. Кинетическая энергия тел переходит при этом в потенциальную энергию деформации и частично в тепловую, энергию звуковых колебаний и другие виды энергии. Вторая фаза — восстановление. Потенциальная энергия деформации превращается в кинетическую энергию тел; тела начинают расходиться и в конце второй фазы соприкосновение тел прекращается.

При ударе абсолютно упругих тел вся кинетическая энергия тел до удара переходит в потенциальную энергию деформации в первой фазе, во второй – потенциальная энергия деформации полностью переходит в кинетическую энергию тел. Это, так называемый, абсолютно упругий удар, при котором суммарная кинетическая энергия тел в конце удара такая же, как и до удара.

Удар совершенно неупругих тел, заканчивающийся на первой фазе, называется абсолютно неупругим ударом. После абсолютно неупругого удара тела движутся вместе с одинаковой скоростью.

Рассмотрим центральный абсолютно упругий удар двух шаров. Пусть шары массой m₁ и m₂ движутся до соударения со скоростями v₁ и v₂, после соударения – со скоростями u₁ и u₂ . На основании законов сохранения импульса в энергии можно записать:

m₁v₁ + m₂v₂ = m₁u₁ + m₂u₂ (1)

m₁v₁² + m₂v₂² = m₁u₁² + m₂u₂² (2)

или с учетом того, что движение шаров происходит по одной прямой,

m₁v₁ – m₁u₁ = m₂u₂ – m₂v₂ (3)

m₁v₁² – m₁u₁² = m₂u₂² – m₂v₂². (4)

Деля (3) на (4), получаем v₁ + u₁ = u₂ + v₂ или v₁ – v₂ = - (u₁ – u₂). (5)

Таким образом, при центральном абсолютно упругом соударении шаров их относительная скорость меняет свое направление на противоположное, но остается неизменной по величине.

Выполняя преобразования, аналогичные предыдущим, получаем для упругого соударения

v₁ – v₂ > - (u₁ – u₂). (6)

Следовательно, при упругом ударе шаров их относительная скорость меняет направление на противоположное и уменьшается при этом по абсолютной величине.

Отношение относительной скорости тел после удара к относительной скорости до удара называется коэффициентом восстановления:

K = (7)

Для абсолютно упругого удара K = 1.

В условиях опыта коэффициент восстановления может считаться величиной, зависящей только от материала соударяющихся тел, следовательно, величиной K можно характеризовать упругие свойства и материал соударяющихся тел. Величину коэффициента восстановления и времени соударения удобно определять при центральном ударе шаров.

1. Пусть два шара одинаковой массы висят на нитях равной длины, касаясь друг друга. Если оба шара отклонить на равные углы и одновременно освободить их, то они, сталкиваясь друг с другом, в любой момент будут иметь скорости, равные по величине, но противоположные по знаку.

Рассчитаем величину скорости.

Для каждого из шаров справедливо (пренебрегаем силами трения): (mv²)/2 = mgh, (8)

где h – высота подъема шара. Но h = L - Lcos = 2Lsin²(/2). (9)

(см. рис.2) Если достаточно мал, то sin²(/2)  (/2)². Тогда

h  2L(/2)² = (²L)/2. (10)

Из (9) и (10) получаем v = , ( - в радианах) (11)

А

Рис.2

налогично определяются скорости шаров после удара.

Учитывая, что v₁ = - v₂ и u₁ = - u₂,

коэффициент восстановления может быть представлен в виде:

K = |u₁ – u₂|/|v₁ – v₂| = |u – (-u)|/|v – (-v)| = |u|/|v|. (12)

Если учесть формулу (11), то

K = ₁/₀, (13)

где ₁ – угол отклонения шара после удара, ₀ – угол отклонения шара до удара.

Уменьшение угла отклонения после первого удара может быть мало, поэтому целесообразно измерить величину угла отклонения после n – го удара. В этом случае формула (13) принимает вид: K = (14)

Действительно, после первого удара K = ₁/₀ , после второго K = ₂/₁ ,после третьего K = ₃/₂ , после n – го соударения K = _n/(_n-1). Почленно перемножив эти равенства, получим формулу (14).

2. Время соударения зависит от относительной скорости шаров в момент удара, упругих постоянных для их материала, а также радиуса шаров.

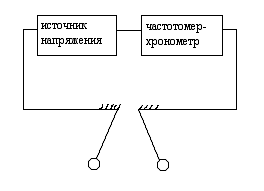Для определения времени соударения существует довольно много методов. В нашей работе используется следующий (см. рис.3).

Рис.3. Блок-схема для измерения времени удара шаров.

Шары включаются последовательно в цепь, содержащую источник постоянного напряжения и частотомер-хронометр. Во время удара сигнал от источника напряжения поступает на вход частотомера, который по длительности поступившего импульса фиксирует время соударения шаров.

3. О степени деформации можно судить по величине энергии, затраченной на эту деформацию.

Действительно, (пренебрегая всякого рода потерями) из закона сохранения энергии имеем

(m₁v₁²)/2 + (m₂v₂²)/2 = (m₁u₁²)/2 + (m₂u₂²)/2 + 2W_о.д. ,

где W_о.д. - энергия остаточной деформации одного шара, относящаяся к одному соударения.

Так как m₁ = m₂; v₁ = - v₂; u₁ = - u₂, то из предыдущего соотношения получим

mv² = mu² + 2W_о.д.,

или W_о.д. = (mv²)(1 – u²/v²)/2 .

Учитывая, что K = |u|/|v|, окончательно получим

W_о.д. = (mv²)(1 – K²)/2. (15)

4. Среднюю силу упругого удара, действующую на шар при ударе, можно рассчитать, зная среднее время соударения шаров и коэффициент восстановления K.

На основании второго закона Ньютона F_y dt = mdv, где F_y – сила упругого удара, действующая на шар.

Удобнее вместо F_y ввести среднюю силу упругого удара F₀ , величина которой во время удара остается постоянной. Тогда

= F₀ = .

После интегрирования получаем F₀ = m(u + v), отсюда

F₀ = mv(K + 1)/. (16)