5. Исследование формы

гиперболы					x2	y2	1	(2)
					a2	b2	1	(2)
					a2	b2
Выразим y из уравнения гиперболы и возьмем
положительное значение			y b	x2 a2			(3)
			a
считая, что	x	a получим точки гиперболы,
считая, что	x	a получим точки гиперболы,
лежащие в I	четверти.
Из уравнения (3) => что y в полуинтервале								a x
есть возрастающая функция при этом предел
lim	y lim b		x2 a2
x		x a

Всякая прямая пересекает гиперболу не более чем в двух точках, так как прямая определяется уравнением I степени, а гипербола - II

гиперболы	x2	y2	1 (2)
	a2	b2

Рассмотрим уравнение прямой y b x		(4) или bx ay 0;
	a

Найдем расстояние d от точки M(x,y), лежащей на дуге гиперболы, определенной уравнением (3), до прямой (4):

гиперболы	x2	y2	1 (2)
	a2	b2

Рассмотрим уравнение прямой y b x		(4) или bx ay 0;
	a

Найдем расстояние d от точки M(x,y), лежащей на дуге гиперболы, определенной уравнением (3), до прямой (4):

b(x

bx ay

bx b x2 a2

x2 a2

a2 b2

x2 x2 a2

a2b

x2 a2

x x2 a2

x2 a2

lim d 0

гиперболы	x2	y2	1	(2)
	a2	b2

Получили, что на полуинтервале	a,			расстояние

d от точки M(x,y) рассматриваемой части гиперболы до прямой (4) есть убывающая функция и

(т.е. расстояние стремиться к 0)

lim d 0

гиперболы	x2	y2	1	(2)
	a2	b2

Получили, что на полуинтервале	a,			расстояние

d от точки M(x,y) рассматриваемой части гиперболы до прямой (4) есть убывающая функция и

(т.е. расстояние стремиться к 0)

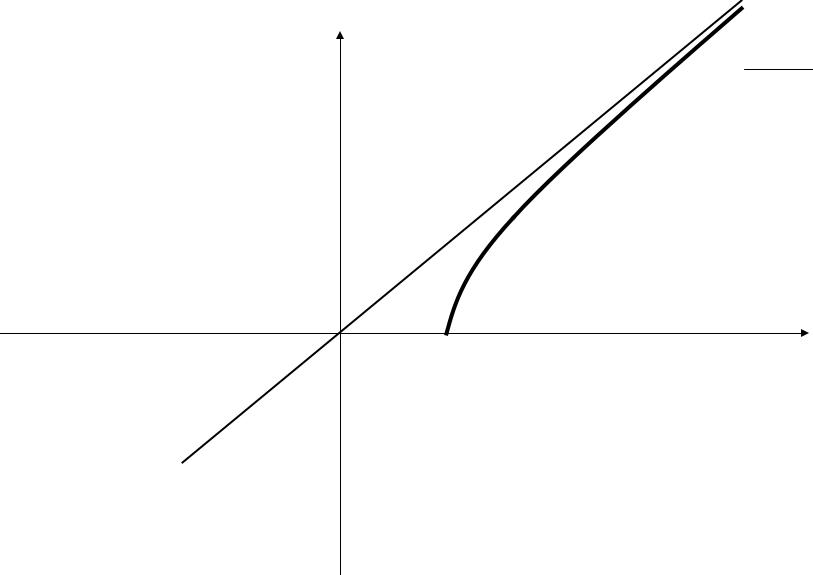
Прямая, определяемая уравнением	y b x (4)
называется асимптотой гиперболы.	a
называется асимптотой гиперболы.