5. Исследование формы гиперболы

5. Исследование формы

Т.к. в каноническое уравнение гиперболы координаты x и y входят во второй степени

5. Исследование формы гиперболы

Т.к. в каноническое уравнение гиперболы координаты x и y входят во второй степени => оси Ox и Oy являются осями симметрии гиперболы, а начало координат центром симметрии.

Геометрически это означает, что между прямыми x=a и x=-a нет точек гиперболы.

Геометрически это означает, что между прямыми x=a и x=-a нет точек гиперболы.

Ось симметрии Oy не пересекает гиперболу и называется мнимой осью.

Ось симметрии Ox пересекает гиперболу в двух точках A1(-a;0) A2(a;0) – вершинах

гиперболы и называется действительной осью.

Ось симметрии Ox пересекает гиперболу в двух точках A1(-a;0) A2(a;0) – вершинах

гиперболы и называется действительной осью.

a и b в уравнении гиперболы называются соответственно действительной и мнимой

полуосями гиперболы.

Выразим y из уравнения гиперболы и возьмем положительное значение 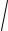x2 a2 (3)

Из уравнения (3) => что y в полуинтервале a x есть возрастающая функция при этом предел

lim y

x

Из уравнения (3) => что y в полуинтервале a x есть возрастающая функция при этом предел

Из уравнения (3) => что y в полуинтервале a x есть возрастающая функция при этом предел

Всякая прямая пересекает гиперболу не более чем в двух точках, так как прямая определяется уравнением I степени, а гипербола - II

Найдем расстояние d от точки M(x,y), лежащей на дуге гиперболы, определенной уравнением (3), до прямой (4):

Найдем расстояние d от точки M(x,y), лежащей на дуге гиперболы, определенной уравнением (3), до прямой (4):

Найдем расстояние d от точки M(x,y), лежащей на дуге гиперболы, определенной уравнением (3), до прямой (4):

Найдем расстояние d от точки M(x,y), лежащей на дуге гиперболы, определенной уравнением (3), до прямой (4):

Найдем расстояние d от точки M(x,y), лежащей на дуге гиперболы, определенной уравнением (3), до прямой (4):

Получили, что на полуинтервале расстояние d от точки M(x,y) рассматриваемой части гиперболы до прямой (4) есть убывающая функция и

(т.е. расстояние стремиться к 0)

d от точки M(x,y) рассматриваемой части гиперболы до прямой (4) есть убывающая функция и

(т.е. расстояние стремиться к 0)

y

x

y ba x

y

y ba x2 a2

x

y ba x

y

y ba x2 a2

M

x

y ba x

y

y ba x2 a2

dM

x

y ba x

y

y ba x2 a2

d

M

x

y ba x