Файловый архив студентов. Файловый архив студентов.
1302 вуза, 5134 предмета.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Челябинский Государственный Университет
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:
лекции-презентации ГЕОМЕТРИЯ / Прямая в пространстве.ppt
Скачиваний:
58
Добавлен:
23.03.2015
Размер:
777.73 Кб
Скачать
☆
►Содержание►

Приведение к каноническому виду

Приведение к каноническому виду

A1x B1 y C1z D1 0A2 x B2 y C2 z D2 0

Приведение к каноническому виду

A1x B1 y C1z D1 0A2 x B2 y C2 z D2 0

Решение системы (x0;y0;z0)

Приведение к каноническому виду

A1x B1 y C1z D1 0A2 x B2 y C2 z D2 0

Решение системы (x0;y0;z0) M (x0;y0;z0) L

L

s

П1

П2

1 : A1x B1 y C1z D1 0

 

2 : A2 x B2 y C2 z D2 0

L

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

s

П1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

П2

 

n1

 

 

 

 

 

1

: A1x B1 y C1z D1

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2 : A2 x B2 y C2 z D2 0

1 : n1 A1; B1;C1

L

s

 

 

 

 

 

 

 

 

П1

 

 

 

 

 

 

 

 

 

 

 

 

n1

 

 

 

 

 

 

П2

 

 

 

 

n2

1 : A1x B1 y C1z D1 0

 

 

 

 

 

 

 

 

 

 

 

 

 

2 : A2 x B2 y C2 z D2 0

1 : n1 A1; B1;C12 : n2 A2 ; B2 ;C2

L

1 : n1 A1; B1;C12 : n2 A2 ; B2 ;C2

s

П1

 

 

 

 

 

 

n1

 

 

 

 

 

n2

П2

 

 

 

 

L

1 : n1 A1; B1;C12 : n2 A2 ; B2 ;C2

 

 

s

 

s

 

 

П1

 

 

 

 

 

 

n1

 

 

 

 

 

n2

П2

 

 

 

 

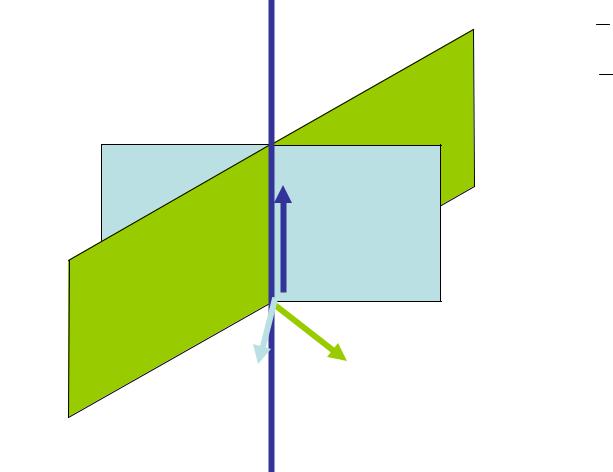
L

1 : n1 A1; B1;C12 : n2 A2 ; B2 ;C2

 

 

 

 

 

1;

 

2

 

 

s

n

n

s

П1

 

 

 

 

 

 

n1

 

 

 

 

 

n2

П2

 

 

 

 

 

 

L

 

 

 

 

 

 

 

 

1 :

 

 

 

1 A1; B1;C1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n

 

 

 

 

 

 

 

 

 

 

 

 

2 :

 

 

2 A2 ; B2 ;C2

 

 

 

 

 

 

 

 

 

 

 

 

n

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1;

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

s

n

n

 

 

 

 

 

 

 

 

s

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

П1

 

 

i j k

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n2

П2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

L

1 : n1 A1; B1;C12 : n2 A2 ; B2 ;C2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1;

 

2

 

 

 

 

 

 

 

 

 

 

 

s

n

n

 

 

 

 

 

 

 

 

s

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

 

j

k

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

П1

 

A1

 

B1

C1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

A2

B2

C2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n2

 

 

 

 

 

 

 

 

 

П2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

L

1 : n1 A1; B1;C12 : n2 A2 ; B2 ;C2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1;

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

s

n

n

 

 

 

 

 

 

 

 

 

 

 

 

 

s

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

 

 

 

 

j

 

 

k

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

П1

 

 

 

 

 

A1

 

 

B1

C1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

A2

 

B2

C2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

B

 

C

 

 

 

C

A

 

 

 

A

B

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n1

 

 

 

 

 

 

 

 

 

 

s

 

1

 

1

 

;

 

1

1

 

;

 

1

1

 

 

 

 

 

 

 

 

 

 

n2

 

 

 

 

 

 

 

 

 

П2

 

 

 

 

 

 

 

 

 

 

 

 

 

B2

C2

 

 

 

C2

A2

 

 

 

A2

B2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

L

1 : n1 A1; B1;C12 : n2 A2 ; B2 ;C2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1;

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

s

n

n

 

 

 

 

 

 

 

 

 

 

 

 

 

s

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

 

 

 

 

j

 

 

k

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

П1

 

 

 

 

 

A1

 

 

B1

C1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

A2

 

B2

C2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

B

 

C

 

 

 

C

A

 

 

 

A

B

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n1

 

 

 

 

 

 

 

 

 

 

s

 

1

 

1

 

;

 

1

1

 

;

 

1

1

 

 

 

 

 

 

 

 

 

 

n2

 

 

 

 

 

 

 

 

 

П2

 

 

 

 

 

 

 

 

 

 

 

 

 

B2

C2

 

 

 

C2

A2

 

 

 

A2

B2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Проверим компланарность вектора s каждой плоскости

Применим необходимое и достаточное условие компланарности вектора s={l;m;n} и плоскости

Ax+By+Cz+D=0

Применим необходимое и достаточное условие компланарности вектора s={l;m;n} и плоскости

Ax+By+Cz+D=0

Al+Bm+Cn=0

Применим необходимое и достаточное условие компланарности вектора s={l;m;n} и плоскости

Ax+By+Cz+D=0

Al+Bm+Cn=0

 

 

 

B

C

 

 

 

C

A

 

 

 

A

B

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n1 A1; B1;C1

s

 

1

1

 

;

 

1

1

 

;

 

1

1

 

 

 

 

 

B2

C2

 

 

 

C2

A2

 

 

 

A2

B2

 

 

 

 

Применим необходимое и достаточное условие компланарности вектора s={l;m;n} и плоскости

Ax+By+Cz+D=0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Al+Bm+Cn=0

 

 

 

l

 

 

 

 

m

 

 

 

 

n

 

 

 

 

 

 

 

 

 

B

C

 

 

 

C

A

 

 

 

A

B

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n1 A1; B1;C1

s

 

1

1

 

;

 

1

1

 

;

 

1

1

 

 

 

 

 

B2

C2

 

 

 

C2

A2

 

 

 

A2

B2

 

 

 

 

 

Применим необходимое и достаточное условие компланарности вектора s={l;m;n} и плоскости

Ax+By+Cz+D=0

Al+Bm+Cn=0

l m n

 

 

 

B

C

 

 

 

C

 

A

 

 

 

 

A

B

 

 

 

 

 

 

A ; B ;C

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

;

 

 

 

;

 

 

 

 

n1

s

 

1

 

 

1

 

 

1

 

1

 

 

 

1

1

 

 

 

 

 

 

B2

C2

 

 

 

C2

 

A2

 

 

 

 

A2

B2

 

 

 

 

 

 

1

1

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

A

B1

C1

 

B

C1

 

A1

 

C

A1

B1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

B

C

2

 

 

 

 

1

C

2

 

 

A

 

1

 

 

A

B

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

2

 

 

 

2

2

 

 

 

 

 

 

Применим необходимое и достаточное условие компланарности вектора s={l;m;n} и плоскости

Ax+By+Cz+D=0

Al+Bm+Cn=0

l m n

 

 

 

 

B

C

 

 

 

C

 

A

 

A

B

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

;

 

;

 

n1

A ; B ;C

s

 

1

 

 

1

 

 

C

1

 

1

1

1

 

 

 

 

 

 

 

B C

 

 

 

 

 

A

 

A

B

 

 

 

 

 

 

1 1 1

 

 

 

 

2

 

 

2

 

 

 

 

2

 

2

 

2

2

 

 

 

 

 

 

A1

B1

C1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

A B1

C1

 

 

 

 

 

 

C1

 

A1

 

C A1

B1

 

 

 

 

 

 

 

 

 

 

 

 

 

B

 

 

 

 

A B C

1

B C

2

 

 

 

1

C

2

A

 

1

 

A B

 

1

1

1

 

 

 

2

 

 

 

 

 

 

 

 

 

2

 

 

2

2

 

 

 

A2

B2

C2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Применим необходимое и достаточное условие компланарности вектора s={l;m;n} и плоскости

Ax+By+Cz+D=0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Al+Bm+Cn=0

 

 

 

 

 

 

 

 

l

 

 

 

 

 

 

 

m

 

 

n

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

B

C

 

 

 

C

 

A

 

A

B

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

;

 

;

 

n1

A ; B ;C

s

 

1

 

 

1

 

 

C

1

 

1

1

1

 

 

 

 

 

 

 

B C

 

 

 

 

 

 

A

 

A

B

 

 

 

 

 

 

1 1 1

 

 

 

 

 

2

 

 

2

 

 

 

 

2

 

2

 

2

2

 

 

 

 

 

 

A1

B1

C1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

A B1

C1

 

B C1

 

A1

 

 

 

 

A1

B1

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

C

 

 

A

B C

1

B C

2

 

 

 

 

1

C

2

A

 

1

 

 

A B

 

1

1

1

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

2

 

 

 

2

2

 

 

 

A2

B2

C2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Применим необходимое и достаточное условие компланарности вектора s={l;m;n} и плоскости

Ax+By+Cz+D=0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Al+Bm+Cn=0

 

 

 

l

 

 

 

 

m

 

 

 

 

n

 

 

 

 

 

 

 

 

 

B

C

 

 

 

C

A

 

 

 

A

B

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n2 A2 ; B2 ;C2

s

 

1

1

 

;

 

1

1

 

;

 

1

1

 

 

 

 

 

B2

C2

 

 

 

C2

A2

 

 

 

A2

B2

 

 

 

 

 

Применим необходимое и достаточное условие компланарности вектора s={l;m;n} и плоскости

Ax+By+Cz+D=0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Al+Bm+Cn=0

 

 

 

 

 

l

 

 

 

 

 

m

 

 

 

 

n

 

 

 

 

 

 

 

 

 

 

 

B

C

 

;

 

C

A

 

;

 

A

B

 

 

 

 

 

A ; B ;C

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n2

s

 

1

 

1

 

 

C

1

1

 

 

1

1

 

 

 

 

 

B C

 

 

 

 

 

A

 

 

 

A B

 

 

 

 

2 2 2

 

 

 

 

2

 

2

 

 

 

 

2

2

 

 

 

2

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

A B1

C1

 

C1

A1

 

 

 

A1

B1

 

 

A2

B2

C2

 

0

 

 

 

 

 

 

 

 

 

 

 

 

B

C

 

 

 

 

A

B C

 

2

B C

2

2

C

A

 

2

 

A B

 

 

1

1

1

 

 

 

2

 

 

 

2

2

 

 

 

2

2

 

 

A2

B2

C2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 
Соседние файлы в папке лекции-презентации ГЕОМЕТРИЯ
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности