
GeomCh
.pdf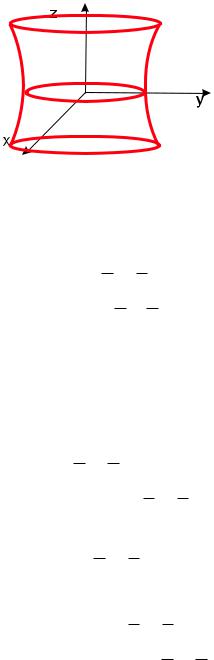
Рис. 38:
7.Эллиптический параболоид: xa22 + yb22 = 2z (рис.41)
8.Гиперболический параболоид: xa22 ¡ yb22 = 2z (В простонародии "седло"). (рис.42)
Цилиндрические поверхности
Цилиндр получается когда отсутствует одна координата в уравнении.
9.Эллиптический цилиндр:xa22 + yb22 = 1 (рис.43)
10.Мнимый эллиптический цилиндр: xa22 + yb22 = ¡1 (При любом z получаем эллипс в сечении)
11.Гиперболический цилиндр: xa22 ¡ yb22 = 1 (рис.44)
12.Параболический цилиндр: y2 = 2z (рис.45)
13.Две пересекающиеся плоскости: xa22 ¡ yb22 = 0 или (xa ¡ yb )(xa + yb ) = 0
14.Мнимые пересекающиеся плоскости: xa22 + yb22 = 0
15.Параллельные плоскости: x2 = a2 две параллельные плоскости x = §a (a 6= 0) на расстоянии 2a
50
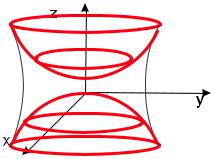
Рис. 39:
16.Мнимые параллельные плоскости: x2 = ¡a2 (a 6= 0)
17.Совпадающие плоскости: x2 = 0
Пример. Определить тип поверхности второго порядка: x2 + 4xy ¡ y2 + 2z ¡ 8xz + 4yx + 5 = 0
(x + 2y ¡ 4z)2 ¡ 5y2 ¡ 14z2 + 20yz + 5 = 0
ПАМЯТКА: а) Подчеркиваем все слагаемые содержащие данное неизвестное. б) (a + b + c + d)2 = a2 + b2 + c2 + d2 + 2ab + 2ac + 2ad + 2bc + 2bd + 2cd:
x02 ¡ 5(y ¡ 2z)2 + 6z2 + 5 = 0 x02 ¡ 5y02 + 6z2 = ¡5
Чтобы определить тип нужно все загнать в квадрат.
51

Рис. 40:
Рис. 41:
52
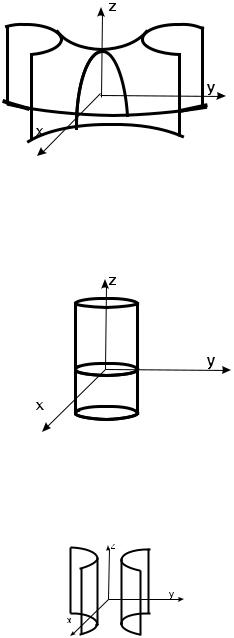
Рис. 42:
Рис. 43:
Рис. 44:
53
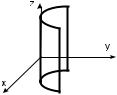
Рис. 45:
54
