
Тема 3. Интервальные оценки.
ЗАДАЧИ
3.1. Измерения случайной величины, распределенной по нормальному закону, дали следующие значения.
|
12.219 |
11.598 |
11.012 |
9.724 |
9.573 |
|
12.941 |
9.649 |
8.033 |
9.230 |
14.310 |
Оценить математическое ожидание, дисперсию. Построить доверительный интервал с уровнем достоверности 0.9.
3.2. Измерения случайной величины, распределенной по нормальному закону, дали следующие значения.
|
-0.48496 |
0.149774 |
-2.06519 |
1.054071 |
-1.13811 |
|
-2.0769 |
-2.04166 |
-2.65699 |
-0.00457 |
0.692439 |
|
0.483049 |
-1.18127 |
1.15884 |
0.747012 |
1.192643 |
|
-0.73544 |
-0.74888 |
-0.0115 |
-0.02853 |
0.231945 |
Построить 95%-ые доверительные интервалы для математического ожидания.
3.3. Пусть дисперсия нормальной случайной величины равна 100. Каков должен быть объем выборки, по которой оценивается математическое ожидание, чтобы ширина 95%-го доверительного интервала была меньше, чем 2.4?
3.4. По результатам 9 независимых измерений произведена оценка величины х, записанная в видех=5.20±0.33. Определить границы 95%-го доверительного интервала.
3.5. По результатам 36 независимых измерений произведена оценка величины х, записанная в видех=5.20±0.33. Определить границы 95%-го доверительного интервала.
3.6. На контрольных испытаниях n=16
ламп была определена средняя
продолжительность работы лампы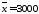 часов. Считая, что срок службы лампы
распределен нормально с
часов. Считая, что срок службы лампы
распределен нормально с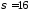 ч, определить доверительную вероятность
того, что точность средней равна 10 ч.
ч, определить доверительную вероятность
того, что точность средней равна 10 ч.
3.7. Случайная величина распределена по
нормальному закону с
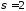 .
Сделана случайная выборка изn=25
элементов. Найти с уровнем достоверности
0.95 интервальную оценку для неизвестного
математического ожидания.
.
Сделана случайная выборка изn=25
элементов. Найти с уровнем достоверности
0.95 интервальную оценку для неизвестного
математического ожидания.
3.8. На контрольных испытаниях n=16
ламп была определена средняя
продолжительность работы лампы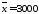 часов и среднее квадратическое отклонение
часов и среднее квадратическое отклонение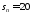 ч. Считая, что срок службы лампы распределен
нормально, определить доверительный
интервал с уровнем достоверности 0.9.
ч. Считая, что срок службы лампы распределен
нормально, определить доверительный
интервал с уровнем достоверности 0.9.
3.9. В результате измерений размеров 25
деталей получены следующие данные:
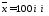 ,
,
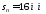 .
Найти уровень достоверности того, что
интервал
.
Найти уровень достоверности того, что
интервал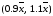 является доверительным интервалом
оценки математического ожидания при
нормальном распределении.
является доверительным интервалом
оценки математического ожидания при
нормальном распределении.
3.10. Случайная величина распределена
нормально с
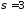 .
Найти минимальный объем выборки, который
обеспечивает точность оценки
математического ожидания 0.3 и уровень
достоверности 0.975.
.
Найти минимальный объем выборки, который
обеспечивает точность оценки
математического ожидания 0.3 и уровень
достоверности 0.975.
Тема 4. Статистическая проверка гипотез.
ЗАДАЧИ
4.1. По выборке из показательного распределения с параметром построить критерий Неймана-Пирсона, различающий гипотезу=1и альтернативную гипотезу=2, если1<2. Вычислить предел мощности построенного критерия приn.
4.2. По выборке из распределения Пуассона с параметром построить критерий Неймана-Пирсона, различающий гипотезу=1и альтернативную гипотезу=2, если1<2. Вычислить предел мощности построенного критерия приn.
4.3. По выборке из биномиального распределения с параметрами mиpпостроить критерий Неймана-Пирсона, различающий гипотезуp=p1и альтернативную гипотезуp=p2, еслиp1<p2. Вычислить предел мощности построенного критерия приn.
4.4. По выборке из геометрического распределения с параметром pпостроить критерий Неймана-Пирсона, различающий гипотезуp=p1и альтернативную гипотезуp=p2, еслиp1<p2. Вычислить предел мощности построенного критерия приn.
Приложение 1.

Приложение 2.
