1.1.5. Функции выпуска продукции; функции затрат ресурсов.

Функции зависимости издержек и дохода от объема производства.

Рассмотрим функции издержек C(q) и дохода фирмы R(q) = qp(q) в зависимости от объема произ­водства q. Поведение функции дохода определяется функцией спроса p(q), рассмотренной выше. Поэтому рассмотрим более подробно по­ведение функции издержек. В типичном случае издержки фирмы велики при небольшом объеме производства q и вначале растут быстрее, чем доход. С увеличением объема производства скорость роста издержек уменьшается, и в какой-то момент они сравнивают­ся с доходом, и фирма начинает получать прибыль. При увеличении объема производства прибыль увеличивается, достигая максимума при оптимальном значении q. При дальнейшем увеличении объема производства издержки снова начинают расти быстрее дохода (исчерпаны эффективные ресурсы, нужны дополнительные помеще­ния, сырье, квалифициро­ванная рабочая сила) и прибыль фирмы умень­шается, достигая отрица­тельных значений при достаточно больших объемах производства. Им, например, могут соответствовать функции R(q) = aq – bq², C(q)=cq – dq² + eq³ . Постройте графики функций дохода, издержек и прибыли.

Распределение налогового бремени.

Пусть р – цена товара на некотором рынке, S(p) – его предложение при цене р, D(p) – спрос. Равновесная цена р₀ определяется уравнением S(р₀)=D(р₀).

Предположим, что вводится дополнительный налог с производителей в размере t с каждой единицы товара. Так как зависимость предложения от цены определяется прибылью, то S_t(p) = S(p – t), где S_t(p) – функция предложения после введения налога. Таким образом, кривая предложения после введения налога сдвигается на t вверх (рис. 1.1.5).

Рис. 1.1.5

Пусть р_t – новая равновесная цена. Равенство спроса и предложения при цене р_t выражается уравнением

S(р_t – t)=D(р_t).

Так как S(p₀) = D(p₀), то из последнего равенства следует

S'(p₀) (p – t)=D'(p₀)p.

Итак, после введения дополнительного налога на покупку единицы товара затраты потребителя увеличатся на величину р, которую можно (приближенно) рассчитать по формуле

Соответственно, доход производителя (также на единицу продукции) уменьшится на

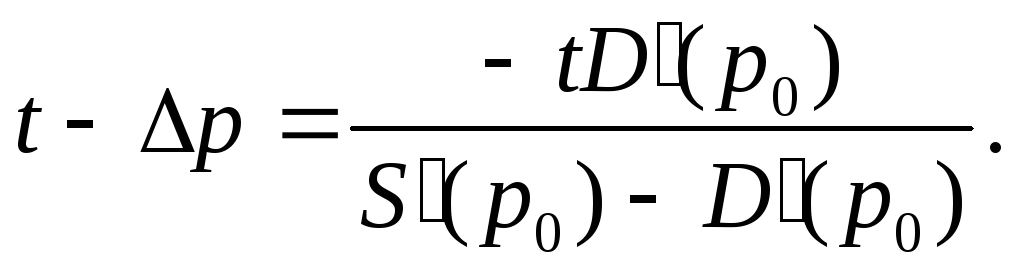
Следовательно, налоговое бремя распределяется между потребителями и производителями продукции в отношении

p:[t–p]=S'(p₀):[ –D'(p₀)],

а поскольку в точке р₀ спрос равен предложению, то

S'(p₀):[ –D'(p₀)]= Е_S:[ – Е_D],

где Е_S, Е_D – коэффициенты эластичности спроса и предложения.

Пример 1.1.6. Пусть ценовая эластичность спроса равна (–3), ценовая эластичность предложения равна 2, а вводимый налог t = 100. Тогда цена после введения этого налога увеличится на 2/(2+3)•100 = 40, а прибыль производителя от единицы продукции уменьшится на 100 – 40 = 60.

Цена, предельные издержки и объем производства.

Пусть q – выпуск продукции (в натуральных единицах); R(q) – выручка от продаж; C(q) – издержки производства, связанные с выпуском q единиц продукции. Тогда прибыль

П(q)=R(q) – C(q).

Предельной выручкой называется выручка от единицы продукции, предельными издержками – издержки от производства единицы продукции. Эти экономические понятия соответствуют значениям производных R'(q) и C'(q).

Предположим, что максимум прибыли достигается в некоторой точке q*0.

Тогда П'(q*) = 0, и в точке q = q* получаем равенство

R'(q*)=C'(q*). (1.1.11)

В экономической теории это равенство вводится как правило, согласно которому фирма, максимизирующая свою прибыль, устанавливает объем производства таким образом, чтобы предельная выручка была равна предельным издержкам.

В случае, когда объем производства q не влияет на цену продукции p, имеем R(q) =pq, R'(q) =p. Равенство (1.1.11) принимает вид

р=C'(q*). (1.1.12)

(для максимизации прибыли необходимо устанавливать такой объем производства, при котором цена была бы равна предельным издержкам).

Пример 1.1.7. Найти оптимальный объем производства, если р=15, C(q)=q³+3q.

Решение. Прибыль при производстве q единиц продукт будет

П(q) = l5q – q³– 3q =q(l2 – q²).

Используя равенство (1.2.2), получим

l5=C'(q*)=3(q*)²+3, откуда q*= 2.

Рассмотрим теперь более общий случай, когда цена продукции является функцией p=p(q) от объема выпуска q.

Из (1.1.11) получим уравнение для цены

R'(q*)=p'(q*)q*+ p(q*)= p(q*)(E_pq(q*)+1)= C'(q*), откуда

(1.1.13)

Так как E_pq(q) < 0, то из равенства (1.1.13) следует, что цена р(q*) больше предельных издержек C '(q*).

Предположим теперь, что фирма является монополией. В этом случае при цене р фирма будет производить столько единиц продукции, сколько требуется покупателям, т.е. q = D(p), где D(p) – функция спроса. Таким образом, функция D(p) будет обратной функцией для функции p(q). Из свойств эластичности следует что E_pq (q*)= (p(q*)).

Пусть p*=p(q*) цена, соответствующая выпуску q*. Тогда уравнение (1.1.13) приобретает вид

(1.1.14)

Пусть, например, E_D = –1.2. Тогда (+1)^–1=(–5/6+1)^–1=6, т.е. цена монополиста р* в 6 раз (!) выше его предельных издержек.

При неэластичном спросе монополия, стремящаяся увеличить свою прибыль, будет снижать объем выпуска. При этом издержки будут снижаться, а цена и прибыль – увеличиваться. В некоторый момент начнется массовый отказ (из-за отсутствия средств) потребителей от продукции данной монополии. Спрос снова станет эластичным.

Пример 1.1.8. Пусть C(q)=0.5q² – издержки фирмы-монополиста, D(p) = 40 – 2p – функция спроса. Найдем зависимость цены р от количества произведенной продукции q. Так как q=D(p) = 40 – 2p, то p=20 – 0.5q. Итак, для функции D(p) мы нашли обратную функцию p(q). Прибыль имеет вид

П(q)=(20 – 0.5q)q – 0.5q²=20q – q².

В точке q* максимума прибыли выполняется равенство П'(q*)=20 – 2q*=0. Находим оптимальный (для монополии) объем производства q*=10. Соответствующая цена будет р* = p(q*)=20 – 0.5q* =15. При этом предельные издержки С'(q*)= 10. Таким образом, цена, наиболее выгодная дли монополии, в полтора раза выше ее предельных издержек. Этот же результат можно получить и по формуле (1.1.14). Проверьте самостоятельно.