Аппроксимация

Сетка и шаблон. Для большинства разностных схем узлы сетки лежат на пересечении некоторых прямых линий (в многомерных задачах – гиперплоскостей), проведенных либо в естественной системе координат, либо в специально подобранной по форме области G.

Если одна из переменных имеет физический смысл времени t, то сетку обычно строят так, чтобы среди ее линий (или гиперплоскостей) были линии t = t_m. Совокупность узлов сетки, лежащих на такой линии или гиперплоскости, называют слоем.

На каждом слое выделяют направления, вдоль которых меняется только одна пространственная координата. Например, для переменных x, y, t есть направления x (t = const, y = const) и направление y (t = const, х = const).

Составляя разностные схемы (26.2) и (26.4), мы использовали во всех внутренних узлах области однотипную разностную аппроксимацию производных. Иными словами, при написании каждого разностного уравнения около некоторого узла сетки бралось одно и то же количество узлов, образующее строго определенную конфигурацию, которую мы назвали шаблоном данной разностной схемы (см. рис. 26.2).

Определение. Узлы, в которых разностная схема записана на шаблоне, называются регулярными, а остальные – нерегулярными.

Нерегулярными являются обычно граничные узлы, а иногда также лежащие вблизи границы узлы (такие, что взятый около этого узла шаблон выходит за границу области).

Составление разностной схемы начинается с выбора шаблона. Шаблон не всегда определяет разностную схему однозначно, но существенно влияет на ее свойства; например, далее мы увидим, что на шаблоне рис. 26.2b нельзя составить хорошей разностной схемы для задачи теплопроводности (26.1). Для каждого типа уравнений и краевых задач требуется свой шаблон.

Явные и неявные разностные схемы

Обсудим вопрос о фактическом вычислении разностного решения. Большая часть физических проблем приводит к уравнениям, содержащим время в качестве одной из переменных. Для таких уравнений ставится обычно смешанная краевая задача, типичным случаем которой является задача теплопроводности (26.1).

К подобным задачам применяют послойный алгоритм вычислений. Рассмотрим его на примере схем (26.2) и (26.4).

В схеме (26.4) 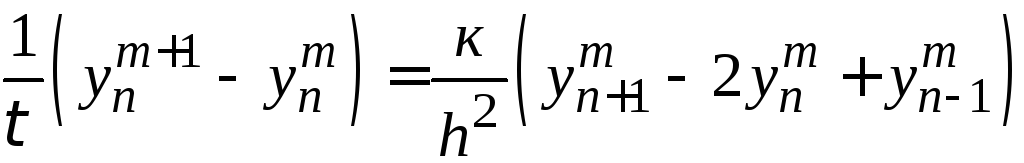на исходном слоеm = 0 решение известно в силу начального условия. Положим m = 0 в уравнениях (26.4). Тогда при каждом значении индекса n уравнение содержит одно неизвестное ; отсюда можно определитьприЗначенияи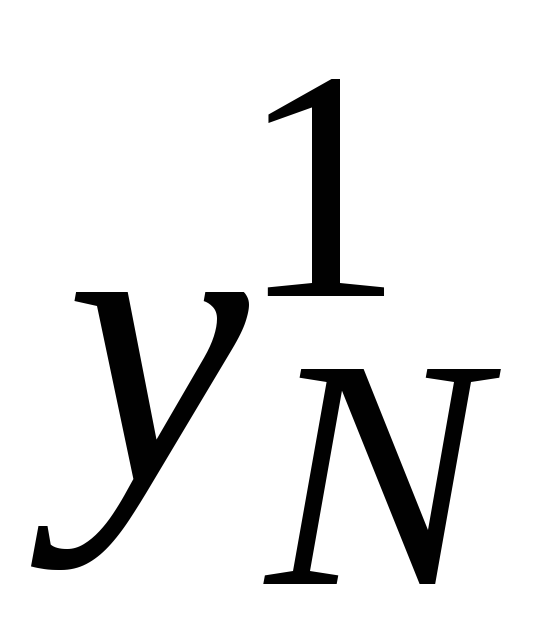определяются по краевым условиям (26.3). Таким образом, значения на первом слое вычислены. По ним аналогичным образом вычисляется решение на втором слое и т.д.

Схема (26.4) в каждом уравнении содержит только одно значение функции на следующем слое; это значение нетрудно явно выразить через известные значения функции на исходном слое, поэтому такие схемы называются явными.

Схема (26.2) 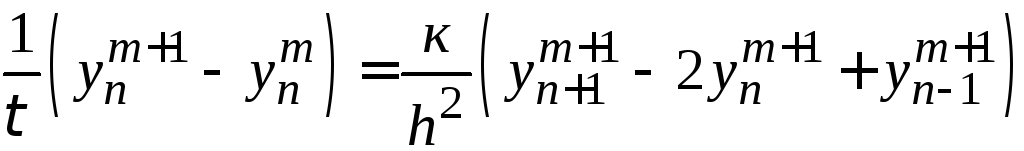содержит в каждом уравнении несколько неизвестных значений функции на новом слое; подобные схемы называются неявными. Для фактического вычисления решения перепишем схему (26.2) с учетом краевого условия (26.3) в следующей форме

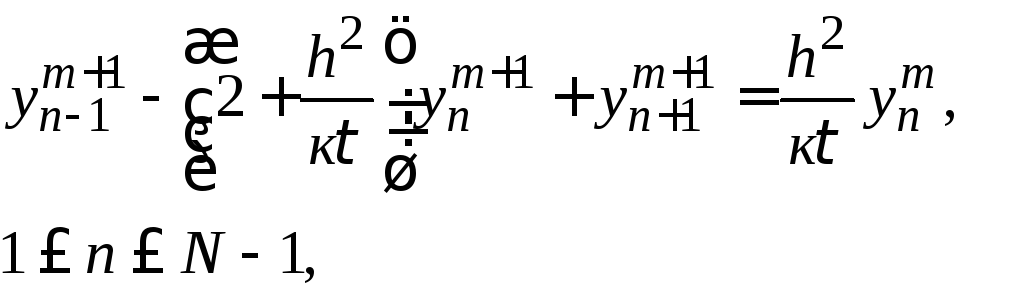(26.5)

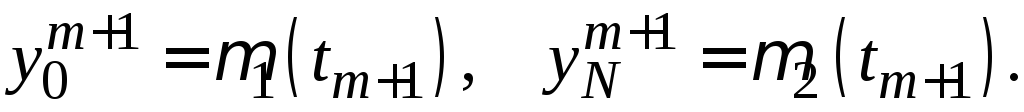
На каждом слое схема (26.5) представляет собой систему линейных уравнений для определения величин 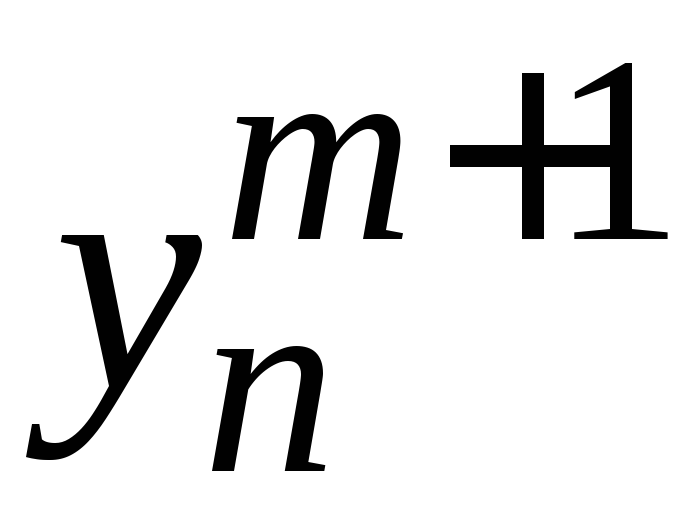; правые части этих уравнений известны, поскольку содержат значения решения с предыдущего слоя. Матрица линейной системы трехдиагональная, и решение можно вычислить алгебраической прогонкой.

Рассмотренный сейчас алгоритм достаточно типичен. Он используется во многих неявных разностных схемах для одномерных и многомерных задач. Дальше мы будем вместо индекса m часто применять сокращенные обозначения

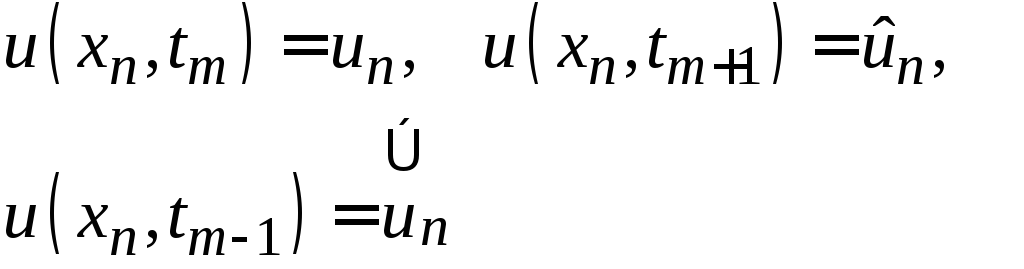
В этих обозначениях явная и неявная разностные схемы принимают соответственно следующий вид

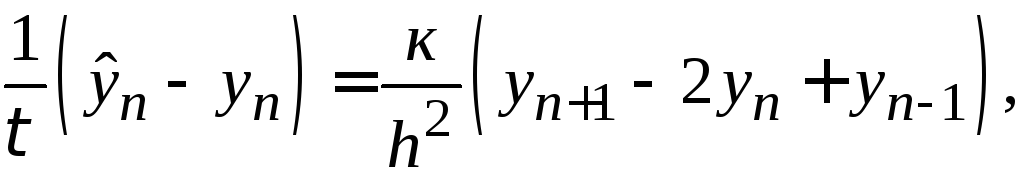
Невязка. Рассмотрим операторное дифференциальное уравнение общего вида (не обязательно линейное)

Au = f, или Au – f = 0.

Заменяя оператор А разностным оператором A_h, правую часть f – некоторой сеточной функцией , а точное решениеu – разностным решением y, запишем разностную схему

или . (26.6)

Если подставить точное решение u в соотношение (26.6), то решение, вообще говоря, не будет удовлетворять этому соотношению . Величину

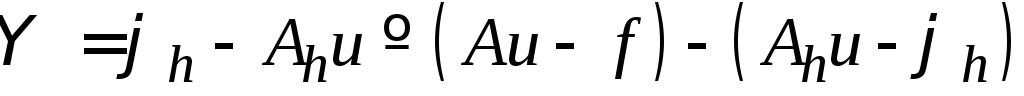
называют невязкой.

Невязку обычно оценивают при помощи разложения в ряд Тейлора. Например, найдем невязку явной разностной схемы (26.4) для уравнения теплопроводности (26.1а). Запишем это уравнение в каноническом виде

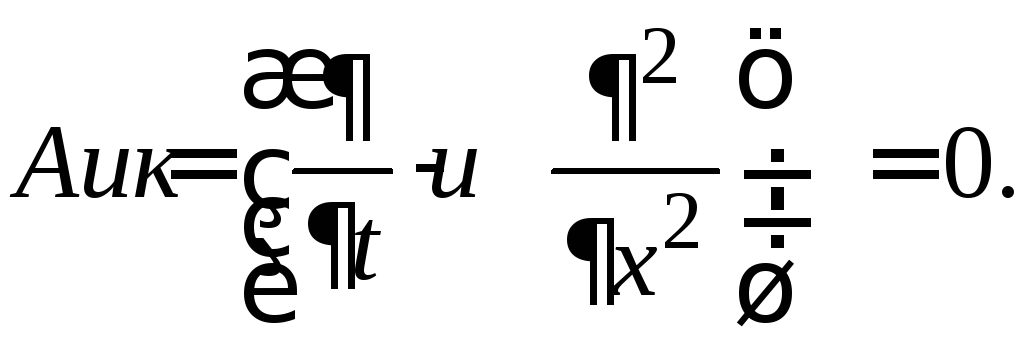
Поскольку в данном случае то

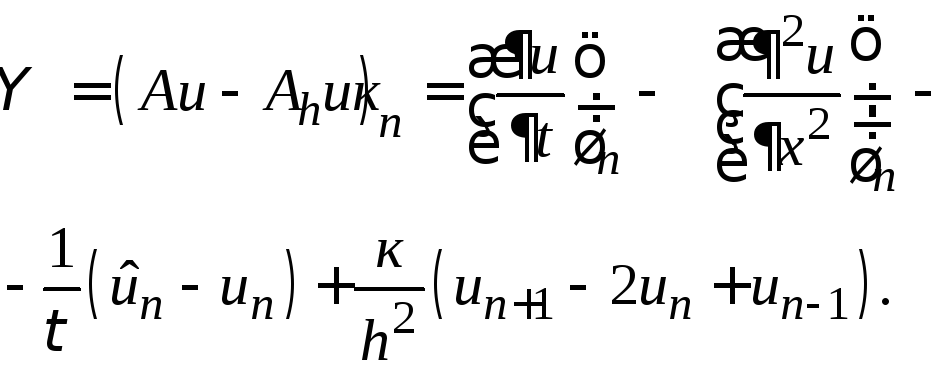
Разложим решение по формуле Тейлора около узла (x_n, t_m), предполагая существование непрерывных четвертых производных по х и вторых по t

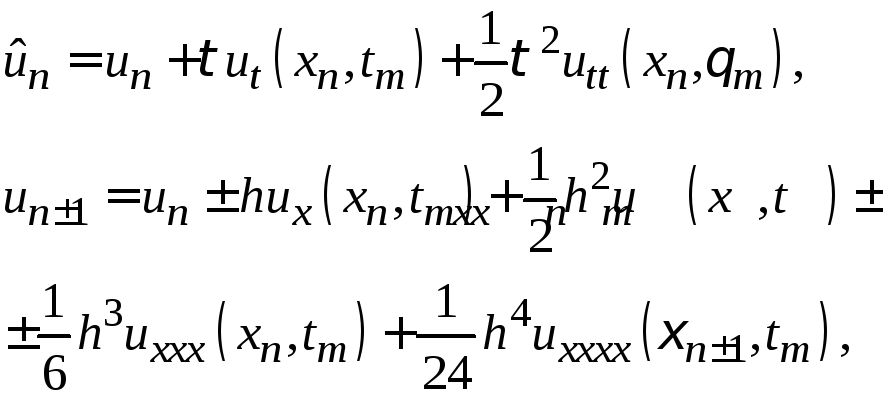(26.7)

где

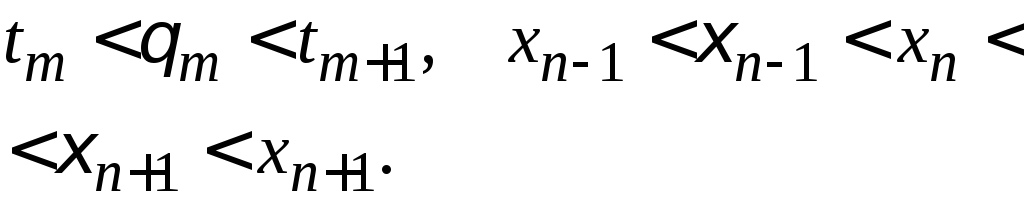
Подставляя эти разложения в выражение невязки и пренебрегая, в силу непрерывности производных, отличием величин 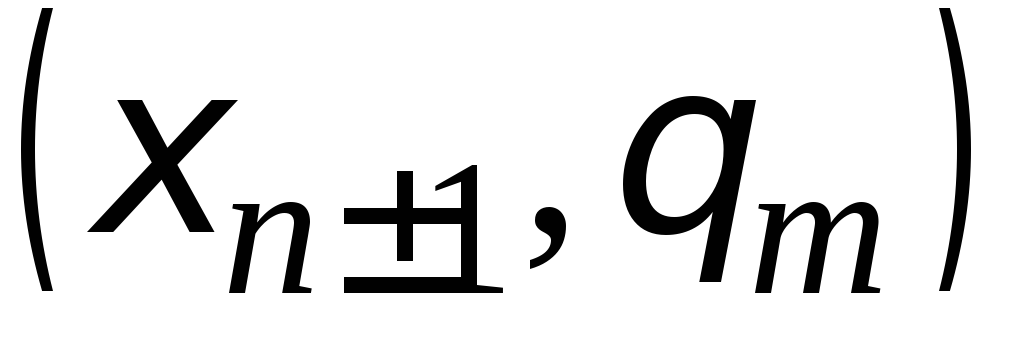от (x_n, t_m) найдем

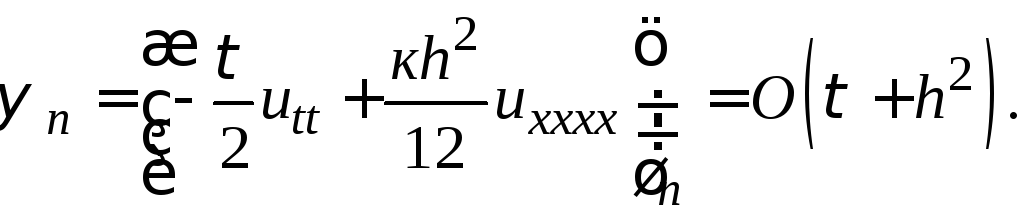(26.8)

Таким образом, невязка (26.8) стремится к нулю при иБлизость разностной схемы к исходной задаче определяется по величине невязки. Если невязка стремится к нулю приh и стремящихся к нулю, то говорят что такая разностная схема аппроксимирует дифференциальную задачу. Аппроксимация имеетр-й порядок, если .

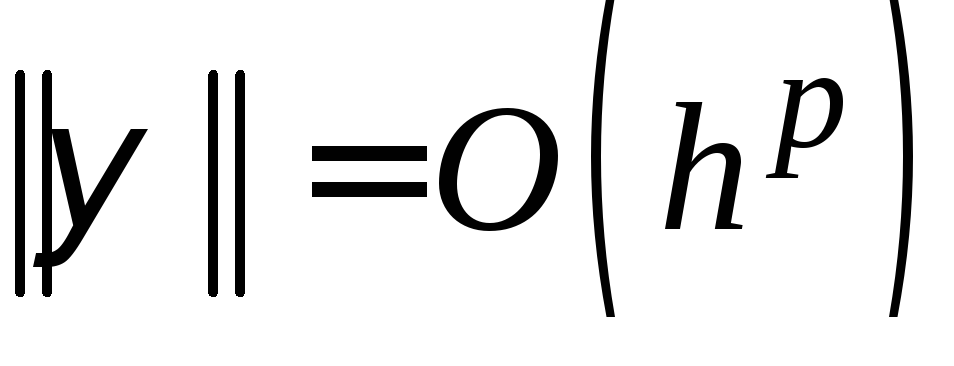Выражение (26.8) дает невязку только в регулярных узлах сетки. Сравнивая (26.3) и (26.1б), легко найдем невязку в нерегулярных узлах

Замечание 1. Решение задачи теплопроводности с постоянным коэффициентом (26.1) в области непрерывно дифференцируемо бесконечное число раз. Однако учет пятых и более производных в разложении в ряд Тейлора (26.7) прибавит к невязке (26.8) только члены более высокого порядка малости поиh, т.е. по существу, не изменит вида невязки.

Замечание 2. Пусть по каким-либо причинам решение исходной задачи дифференцируемо небольшое число раз; например, в задачах с переменным коэффициентом теплопроводности, гладким, но не имеющим второй производной, решение имеет лишь третьи непрерывные производные. Тогда в разложении в ряд Тейлора (26.7) последними будут члены 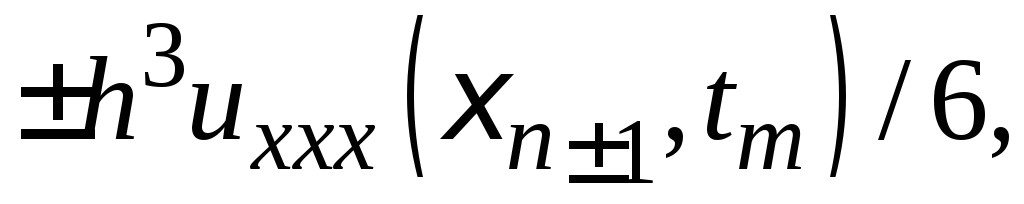не точно компенсирующие друг друга. Это приведет к появлению в невязке (26.8) члена типа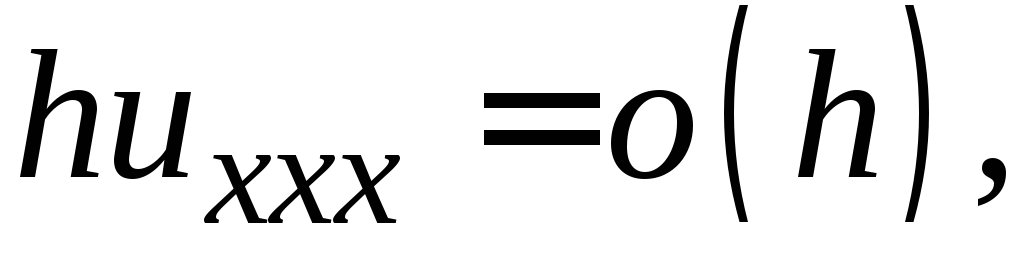т.е. невязка будет иметь меньший порядок малости, чем для четырежды непрерывно дифференцируемых решений.

Замечание 3. Преобразовав выражение невязки с учетом того, что входящая в него функция u(x,t) есть точное решение исходного уравнения и для нее выполняются соотношения

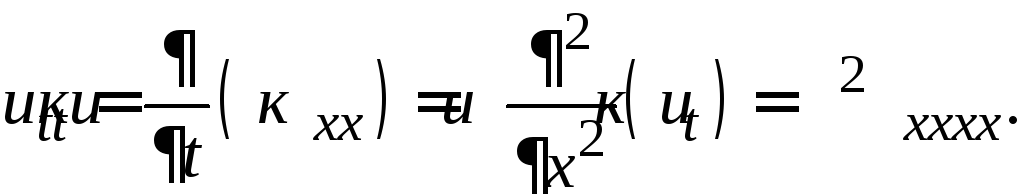
Подставляя это выражение в (26.8), получим

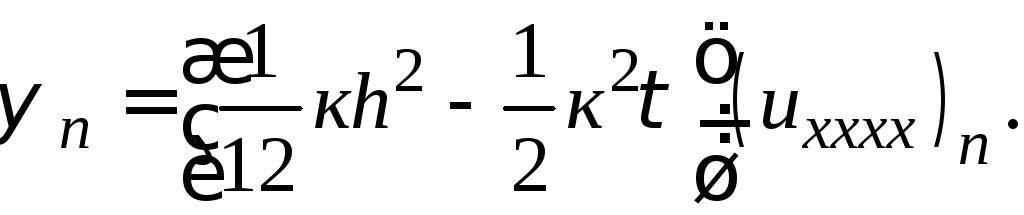
Если выбрать шаги по пространству и времени так, чтобы 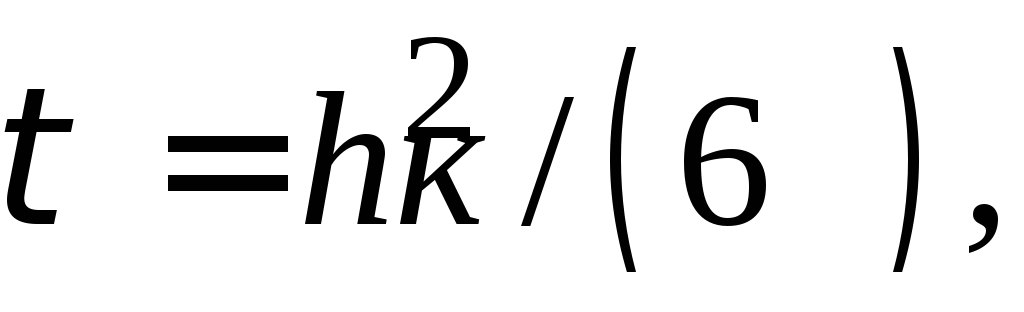то главный член невязки обратится в нуль и останутся только члены более высокого порядка малости поиh (которые мы опускали). Этим приемом пользуются при построении разностных схем повышенной точности.

212