2.1.6. Хвильова природа електрона. Електронні хмари

У 20-х рр. ХХ ст. завдяки роботам де Бройля, Шредінгера, Гейзенберга та інших вчених були розроблені основи хвильової теорії про двоїсту корпускулярно-хвильову природу світлового випромінювання. Ейнштейн довів, що випромінювання є потоком неподільних матеріальних частинок (фотонів), енергія яких визначається рівнянням Планка.

Із рівнянь Планка (E=h) і Eйнштейна (E=mc²) випливає, що h=mc². Враховуючи, що =с/ і швидкість руху фотона v дорівнює швидкості світла с, одержимо основне рівняння хвильової механіки – рівняння де Бройля:

. (11)

Із цього рівняння випливає, що частинці масою m, яка рухається із швидкістю v, відповідає хвиля довжиною . Рівняння (11) можна застосовувати для ха-рактеристики руху не лише фотона , а й інших матеріальних мікрочастинок: електрона, нейтрона, протона тощо.

Отже, електрон одночасно є і частинкою, і хвилею. У 1925 р. Гейзенберг запропонував принцип невизначеності, згідно з яким не можна одночасно встановити точне місцезнаходження електрона в просторі та його швидкість, або імпульс.

Нове уявлення про електрон примусило відмовитись від прийнятої раніше моделі атома, за якою електрон рухається по певних колових або еліптичних орбіталях.

Електрон може знаходитися в будь-якій частині простору, який оточує ядро атома, однак ймовірність його місцезнаходження в тій чи іншій частині атома неоднакова.

Рух електрона має хвильовий характер, тому квантова механіка описує цей рух в атомі за допомогою хвильової функції , яка набуває різних значень у різних точках атомного простору. Відомо, щоб знайти точку в просторі, треба визначити її координати x, y, z, що математично записується залежністю = f(x,y,z).

Оскільки рух електрона хвилеподібний, визначення хвильової функції зводиться до знаходження амплітуди електронної хвилі.

Рух електронної хвилі кількісно характеризується амплітудою , яку можна обчислити з диференціального рівняння Шредінгера, що пов’язує хвильову функцію  з потенціальною і повною енергією електрона. Для одноелектронного атома гідрогену рівняння Шредінгера має такий вигляд:

,(12)

де m –маса електрона;h – стала Планка; Е – повна енергія електрона; U – потенціальна енергія електрона.

Для атомів з кількома електронами застосовують наближене рівняння Шредінгера. Треба зазначити, що допустимі розв’язки рівняння (12) можливі тільки для певних дискретних значень енергії електрона. Кожній із функцій ₁, ₂, ₃,..., _n, які є розв’язками хвильового рівняння, відповідає певне значення енергії Е₁, Е₂, Е₃, ..., Е_n.

За рівнянням (12) можна обчислити -амплітуду електронної хвилі (хвильову функцію). Квадрат амплітуди ² виражає ймовірність місцезнаходження електрона в певній точці атомного простору, а величина ²dV – ймовірність місцезнаходження електрона в елементі об’єму dV.

Як модель стану електрона в атомі у квантовій механіці прийнято уявлення про електронну хмару, густина відповідних ділянок якої пропорційна ймовірності перебування там електрона. Електрон ніби “розмазаний” навколо ядра по сфері, віддаленій від нього на певну відстань. Одна з можливих форм електронної хмари атома показана далі (рис. 9).

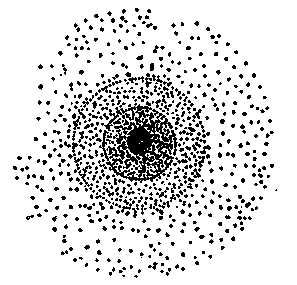Максимальна електронна густина відповідає найбільшій імовірності місцезнаходження електрона, тобто визначається величиною ². Очевидно, чим міцніший зв’язок електрона з ядром, тим електронна хмара менша за розміром і компактніша за розподілом заряду.

П

Рис. 9. Електронна хмара

1s-електрона

ростір навколо ядра, у якому найімовірніше перебуває електрон, називаєтьсяорбіталлю. Таке тлумачення орбіталі дещо спрощене. Орбіталь – математичне поняття, зміст якого випливає із хвильового рів-

няння. Тому можна вважати, що хвильова функція, яка є розв’язком рівняння Шредінгера, називається орбіталлю.

Отже, ядро атома оточене електронними хмарами. Основні характеристики, які визначають рух електрона навколо ядра,  це його енергія і просторові особливості відповідної йому орбіталі.