
МААТЛОГИКА
.pdf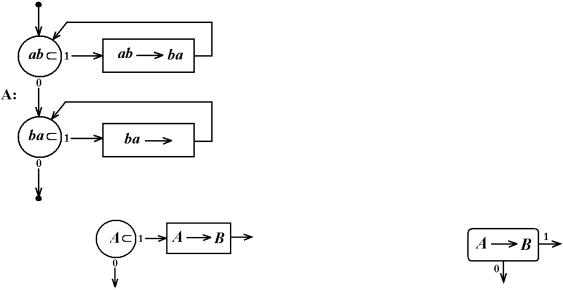
5.2 Нормальнi алгоритми
Поняття про нормальний алгоритм. Узагальнений нормальний алгоритм. Нормальнi алгоритми Маркова. Приклади нормальних алгоритмiв. Принцип нормалiзацi¨. Операцi¨ над алгоритмами. Поняття про унiверсальний нормальний алгоритм.
1. Нехай A ¹ деякий алфавiт. На множинi слiв над цим алфавiтом WA розглянемо
операцiю пiдстановки слiв, тобто операцiю замiнювання одного слова iншим, яка для довiльних слiв A; B 2 WA познача¹ться через A ! B àáî A ! ¢B, äå ñòðiëêà ! i
крапка ¢ не ¹ лiтерами алфавiту A. Застосування операцi¨ пiдстановки до даного слова X зводиться до того, що перше (злiва) входження слова A в слово X замiню¹ться словом B. Наприклад, якщо X = Y AZ, то в результатi застосування пiдстановки
A ! B àáî A ! ¢B äî X ми отриму¹мо слово X1 = Y BZ. Пiдстановка A ! B назива¹ться простою, а A ! ¢B заключною. Нехай A ! (¢) B означа¹ якусь одну
з цих пiдстановок. Скiнченний список пiдстановок в алфавiтi A назива¹ться схемою алгоритму i породжу¹, так званий, алгоритм A в алфавiтi A, який познача¹ться так:
Пiдстановка A !(¢) B не завжди застосовна до слова X, òîìó,
щоб визначити, коли вона застосовна, а коли не застосовна, A: розглядають предикат A ½ X, значення якого дорiвню¹ 1, якщо слово A входить в X, тобто ¹ його пiдсловом, i дорiвню¹ 0, ÿêùî
A не входить в X. Введемо тепер операцiю входження даного слова A, яка познача¹ться A ½, результат застосування яко¨ до слова X ¹ значення
предиката A ½ X. В нормальних алгоритмах ¹диними допустимими операцiями ¹
операцiя пiдстановки та операцiя входження. Нормальнi алгоритми визначаються послiдовнiстю операцiй входження та вiдповiдних ¨м операцiй пiдстановок iз вказiвкою порядку ¨х виконання. Узагальнений нормальний алгоритм в даному алфавiтi A
зада¹ться граф-схемою, в якiй D-точкам вiдповiдають операцi¨ пiдстановки, а P -
точкам операцi¨ входження.
Приклад. На рисунку зображена граф-схема узагальненого нормального алгоритму в алфавiтi fa; bg. Розглянемо слово X = bbaba i застосу¹мо
до нього алгоритм A. Спочатку вiдмiтимо входження слова ab ó ñëîâi X. Ìà¹ìî X = bbaba. Застосувавши першу пiдстановку до нього,
отриму¹мо X1 = bbbaa. Застосу¹мо до X1 другу |
|
пiдстановку, пiсля чого матимемо X2 = bba, çâiäêè |
|
знову за другою пiдстановкою отриму¹мо слово |
|
X3 |
= b, до якого жодна пiдстановка не застосовна. |
Îòæå, A(bbaba) = b. |
|
Äàëi çàìiñòü |
будемо малювати так: |
71
Тодi алгоритм A зобразиться так:
2. Нормальнi алгоритми А. А. Маркова визначаються граф-схемами, якi задоволь- |
|||||
няють умови: |
|
|
|
|
|
а) Об'¹днанi вузли, упорядкованi лiнiйно так, що стрiлка з вiдмiткою 0 одного |
|||||
об'¹днаного вузла входить в наступний об'¹днаний вузол. В перший об'¹днаний вузол |
|||||
входить стрiлка з початково¨ точки граф-схеми. З останнього вузла стрiлка входить в |
|||||
заключну точку схеми. |
|
|
|
|
|
б) Всi стрiлки з вiдмiткою 1 входять або в перший об'¹днаний вузол, або в заключну |
|||||
точку граф-схеми. |
|
|
|
|
|
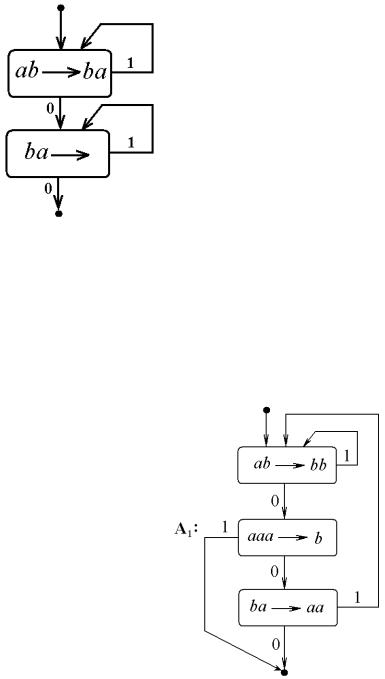
Приклад 1. Розглянемо алгоритм, який зада- |
|||||
ний такою схемою пiдстановок: |
|
|
|||
ab ! bb; |
|
|
|||
A1: 8 aaa !¢ b; |
|
|
|||
< ba |
! |
aa: |
|
|
|
: |
|
|
|
|
|
Граф-схема цього алгоритму зображена на |
|||||
рисунку справа. Розглянемо слово X |
= abba â |
||||
алфавiтi A = fa; bg i застосу¹мо до нього алгоритм |
|||||
A1. Застосувавши до |
слова X = abba |
першу |
|||
пiдстановку, ми отрима¹мо слово X1 |
= |
bbba, |
|||
звiдки за третьою |
пiдстановкою |
матимемо |
|||
X2 = bbaa. До слова X2 застосовна лише третя |
|||||
пiдстановка, тому воно перетворю¹ться у слово |
|||||
X3 = baaa. До слова X3 |
застосовнi друга i третя |
||||
пiдстановки, причому спочатку повинна виконуватись друга пiдстановка, але оскiльки вона ¹ заключною, то на цьому процес перетворення слiв закiнчу¹ться. Отже, слово X3
переходить у слово X4 = bb. Таким чином, A1(abba) = bb. Приклад 2. Розглянемо тепер алгоритм
пiдстановок: |
aba |
bb; |
|
|
|||
A2: |
8 bb |
|
!a; |
|
< aa |
! b: |
|
|
: |
! |
|
72
Застосувавши його до слова X = babbbaa, ми отрима¹мо наступну послiдовнiсть слiв,
кожне з яких отриму¹ться з попереднього слова за однi¹ю з пiдстановок алгоритму A2:
X1 = baabaa, X2 = babba, X3 = baaa, X4 = bba, X5 = aab, X6 = b. Îòæå, A2(babbbaa) = b.
Будемо казати, що алгоритм A застосовний до слова X, якщо про це перетворення слова X закiнчу¹ться пiсля скiнченного числа крокiв яким-небудь словом Y . В цьому випадку говорять, що алгоритм A перетворю¹ слово X в слово Y i цей факт записують як A(X) = Y . Якщо процес перетворення слова X алгоритмом A нiколи не закiнчу¹ться то кажуть, що алгоритм A не застосовний до слова X.
Приклад 3. Алгоритм A3: f! a не застосовний до жодного слова, оскiльки процес приписування злiва лiтери a буде нескiнченним. Зауважимо, що алгоритм A4: f! ¢ a застосовний до будь-якого слова X. Вiн припису¹ злiва до X ëèøå îäíó ëiòåðó a.
Приклад 4. В алфавiтi fa; bg нормальний алгоритм A5: fa ! aa не застосовний до слiв, в якi входить лiтера a, i застосовний до слiв, якi складаються лише з лiтер b.
Необхiдною умовою можливостi побудови нормальних алгоритмiв , якi реалiзують який-небудь конструктивно заданий процес перетворення слiв, ¹ використання обох видiв пiдстановок як звичайних, так i заключних.
Покажемо необхiднiсть заключних пiдстановок. Нехай A ¹ нормальний алгоритм,
у якого нема¹ заключних пiдстановок; X слово, до якого застосовний алгоритм A, тодi, очевидно, ма¹ мiсце рiвнiсть
A(A(X)) = A(X); |
(5.2.1) |
тобто результат дi¨ на слово A(X) ¹ знову слово A(X), оскiльки до нього вже не
застосовнi всi пiдстановки алгоритму A. Умовi (5.2.1) не задовольня¹ алгоритм Aa,
äå Aa(X) = aX, îñêiëüêè Aa(Aa(X)) = Aa(aX) = aaX. Алгоритм Aa, таким
чином, не може бути реалiзований нормальним алгоритмом зi схемами без заключних пiдстановок. В той же час ясно, що алгоритм A4: f!¢ a застосовний до кожного слова
X.
По кажемо тепер, що неможливо обмежитись лише одними заключними пiдстановками. Дiя нормального алгоритму з лише одними заключними пiдстановками, поляга¹ з одноразового застосування однi¹¨ з пiдстановок. Тому довжина вихiдного слова A(X) вiдрiзня¹ться вiд довжини вхiдного слова X на скiнченне число лiтер N, ÿêà
не залежить вiд довжини вхiдного слова X. Число N визнача¹ться як максимум модулiв рiзницi мiж довжинами слiв в лiвiй i правiй частинах пiдстановок алгоритму A.15 Â òîé
же час iснують алгоритми, для яких рiзниця мiж довжинами вхiдного i вихiдного слiв |
|||||||||||
залежить вiд довжини вхiдного слова i може бути як завгодно великою. Наприклад, для |
|||||||||||
алгоритму подво¹ння слiв Apod(X) = XX. Цей алгоритм не може бути реалiзований |
|||||||||||
нормальним алгоритмом, що склада¹ться тiльки iз заключних пiдстановок. |
|
|
|
|
|
||||||
3. Розглянемо деякi приклади нормальних алгоритмiв. |
|
|
|
|
|
|
|
|
|||
|
|
8 |
X1 !¢ Y1; |
|
|
|
|
|
|
||
15 Тобто, якщо ма¹мо алгоритм iз заключними пiдстановками A: |
òî ni = |
j |
l(Xi) |
¡ |
l(Yi) |
, |
|||||
i = 1; : : : ; k, N = max(n1; : : : ; nk) |
|
jl(X) ¡ l(A(X))j 6 N äëÿ |
< |
X¢ ¢k¢ ¢ ¢ ¢ ¢ ¢Y¢k; |
|
X. |
|
j |
|
||
|
: |
!¢ |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
, à òîìó |
|
довiльного слова |
|
|
|
|
|
|
||
73
Приклад 5. Додавання натуральних чисел. Алфавiт: fj; +g. Розглянемо
нормальний алгоритм A1: f+ ! i продемонстру¹мо як викону¹ться дiя 2 + 3 = 5. За початкове слово вiзьмемо X = jj + jjj i застосу¹мо до нього алгоритм A1, ми отрима¹мо слово X1 = jjjjj. Îòæå, A1(X) = X1.
Приклад 6. Вiднiмання½натуральних чисел. Алфавiт: fj; ¡g. Нормальним алгорит-
j ¡ j ! ¡;
¡ !; i продемонстру¹мо його роботу на прикладi 5 ¡3 = 2. За початкове слово вiзьмемо X = jjjjj¡jjj. Застосовуючи послiдовно три рази
першу пiдстановку, ми отрима¹мо такi слова: X1 = jjjj¡jj, X2 = jjj¡j, X3 = jj¡. До слова X3 застосовна лише друга пiдстановка, тому ми ма¹мо X4 = jj. Îòæå, A2(X) = X4.
Приклад 7. Множення двох натуральних чисел. Алфавiт: fj; £; a; bg. Нормальний алгоритм множення позначимо через A3, i вiн визнача¹ться такою системою
пiдстановок: |
|
|
|
|
|
третя пiдстановка, тому слово |
|
|
перетворю¹ться в слово |
|
|
|
|||||||||||||||
|
8 |
b |
|
|
|
b; |
|
|
|
|
|
|
|||||||||||||||
|
> |
|
j ! j |
|
|
|
. За вихiдне вiзьмемо слово |
|
|
|
|
|
. До нього застосовна |
||||||||||||||
|
a |
|
|
|
ba; |
6 |
. До слова |
|
в порядку розташування пiдстановок застосовна |
||||||||||||||||||
|
> |
|
|
|
|
|
|
|
|
|
|
X = jj £ jjj |
|
|
|
|
|
|
|||||||||
A : |
|
|
|
|
|
|
; |
друга пiдстановка, тому |
|
перетворю¹ться в слово |
|
|
|
, |
|||||||||||||
|
> |
|
|
|
|
|
|
a; |
|
|
X1 |
|
|||||||||||||||
|
> j ! j |
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
= j£ |
|||||||||
|
> |
|
|
; |
|
|
|
a |
|
|
X1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
> j£ ! £ |
|
jjj |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
> |
£j ! £ |
|
|
|
|
|
|
X1 |
|
|
|
|
|
|
|
X2 = ba |
|
||||||||||
|
> |
|
слово X3 |
= |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
> a !; |
|
|
|
|
|
|
b ba . Äî X3 вже застосовна перша пiдстановка, |
|||||||||||||||||||
|
< |
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j£j jj |
|
|
|
> b |
|
|
|
|
|
пiсля чого за тi¹ю ж самою пiдстановкою X2 перетворю¹ться в |
||||||||||||||||||||
|
> |
£ ! |
|
|
|
|
|
||||||||||||||||||||
|
|
! j |
|
|
|
|
тому ми отриму¹мо слово |
X4 = |
|
bba |
. Äî |
X4 застосовна друга |
|||||||||||||||
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j £ jj j |
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
> |
|
|
|
|
|
|
|
|
|
j £ j j j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
пiдстановка, |
|
òîìó |
ìè äàëi |
матимемо |
X5 |
|
= |
j |
£ jjbbjba |
. |
Продовжуючи i |
äàëi |
|||||||||||||||
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
подiбнi мiркування, ми послiдовно за тi¹ю чи iншою пiдстановкою отриму¹мо таку послiдовнiсть слiв:
X6 |
= j £ jjbjbba |
X13 |
|
X7 |
= j £ jjjbbba |
X14 |
|
X8 |
= £ajjjbbba |
X15 |
|
X9 |
= £jbajjbbba |
X16 |
|
X10 |
= £jbjbajbbba |
X17 |
|
X11 |
= £jjbbajbbba |
X18 |
|
X12 |
= £jjbbjbabbba |
X19 |
|
= £jjbjbbabbba |
X20 = bbbbbb |
|
= £jjjbbbabbba |
X21 = jbbbbb |
|
= £jjbbbabbba |
X22 = jjbbbb |
|
= £jbbbabbba |
X23 |
= jjjbbb |
= £bbbabbba |
X24 |
= jjjjbb |
= bbbabbba |
X25 |
= jjjjjb |
= bbbbbba |
X26 |
= jjjjjj |
Отже, ми показали, що A3(X) = X26, тобто A3 |
(jj £ jjj) = jjjjjj, що означа¹ 2 £ 3 = 6. |
||||||||||||||||||||||||||||
|
Приклад 8. Алгоритм скасування частини слова. Такий |
|
|
8 aa¯ |
! a¯a; |
||||||||||||||||||||||||
A4(P ® Q) = P для довiльних слiв P; Q в алфавiтi A, äå ® |
|
A. |
|
|
|||||||||||||||||||||||||
алгоритм, який |
ìè |
познача¹мо через |
A4, визнача¹ться |
òàê: |
|
|
> |
ab¯ |
|
|
|
|
b¯a; |
||||||||||||||||
A зада¹ться такою системою пiдстановок: |
® |
|
|
; äå |
a |
|
A. |
|
|
> |
|
|
|
! |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
®a |
|
|
®; |
|
|
62 |
|
|
|
> ba¯ ! a¯b; |
||||||||||
|
|
|
|
|
|
|
|
|
½ |
|
|
|
|
|
|
2 |
|
|
|
|
> |
|
|
|
! |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
Приклад 9. |
Алгоритм подво¹ння слiв. |
|
Розглянемо в |
A |
: |
> |
|
|
|
|
|
|
|
|
||||||||||||||
алфавiтi |
|
|
|
|
, алгоритм подво¹ння |
ñëiâ |
|
|
|
|
|
5 |
|
> |
®b |
! |
b¯b®; |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
||||||||||||||
4 |
|
A = a; b |
|
|
|
|
|
|
! |
|
A5(X) = |
|
|
> bb¯ |
|
|
|
|
b¯b; |
||||||||||
|
|
|
|
|
|
|
! |
|
|
|
|
> |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
f |
|
g |
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
! |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
< |
®a |
a¯a®; |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
; |
|
||||||
нормального алгоритму, що знаходиться праворуч. Нехай X = |
|
|
> |
° |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
¹ вихiдне слово в даному алфавiтi |
|
, òîäi |
|
|
|
|
|
|
|
|
. |
|
|
> |
® |
! |
|
; |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|||||||||||
XX. Цей алгоритм реалiзу¹ться в алфавiтi fa; b; ®; ¯; °g схемою |
|
|
> |
¯ ! °; |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
!¢ |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
®: |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
Процес перетворення |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
! |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
||
вихiдного слова алгоритмом буде такий: |
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|||||||
bab |
|
|
|
|
|
|
A |
|
|
A6 |
(bab) = babbab |
|
|
|
> |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
74

X1 = ®bab, X2 = b¯b®ab, X3 = b¯ba¯a®b, X4 = b¯a¯ba®b, X5 = b¯a¯bab¯b®, X6 = b¯a¯bb¯ab®, X7 = b¯a¯b¯bab®, X8 = b°a¯b¯bab®, X9 = b°a°b¯bab®,
X10 = b°a°b°bab®, X11 = ba°b°bab®, X12 = bab°bab®, X13 = babbab®, X14 = babbab.
Îòæå, A6(X) = X14.
|
|
Приклад 9. Алгоритм подво¹ння слiв в алфавiтi двiйникiв. Алфавiт A = fa; bg, |
||||||||||||||||||||||||||||||||||||||
алфавiт |
äâiéíèêiâ |
A |
= fa; |
b |
g. Алгоритм подво¹ннi слiв в алфавiтi двiйникiв позна- |
|||||||||||||||||||||||||||||||||||
|
|
|
|
8 aa ! aa; |
то це слово в алфавiтi двiйникiв ма¹ вигляд X |
= a b a. Таким |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
ab ! ba; |
чимо через A6 |
. Якщо, наприклад, ми ма¹мо слово X = aba, òî |
|||||||||||||||||||||||||||||||||
|
|
|
|
> ba |
|
|
|
ab; |
чином, A6(X) = XX, тобто A6(aba) = a b aaba. |
|
Розглянемо тепер |
|||||||||||||||||||||||||||||
|
|
|
|
> |
|
|
|
|
|
|
! |
|
|
|
|
|
|
процес перетворення слiв цим алгоритмом слова |
|
. В результатi |
||||||||||||||||||||
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
: |
> |
|
|
|
|
|
! |
|
|
|
|
|
|
ми повиннi отримати слово |
|
|
|
, тобто |
|
|
|
|
|
|
|
. До слова |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
6 |
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
! |
|
|
|
|
|
X = ab застосовна лише остання пiдстановка, тому ми отриму¹мо |
|||||||||||||||||||||||
|
|
|
|
< |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
> bb |
|
|
|
|
bb; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ab |
|
|
|
||||||||
|
|
|
|
> |
®a |
|
|
|
aa®; |
|
|
|
|
|
|
|
|
|
|
|
a b ab |
|
A6(ab) = a b ab |
|
||||||||||||||||
|
|
|
|
> |
® |
|
|
|
!; |
|
|
|
наступне слово X1 = ®ab. На слово X1 дi¹ лише п'ята пiдстановка, |
|||||||||||||||||||||||||||
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
!¢ |
|
|
|
|
|
|
çà ÿêîþ ìè ìà¹ìî |
|
|
. За шостою пiдстановкою слово |
||||||||||||||||||||||
|
|
|
|
> |
®b |
|
® : |
|
|
bb®; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
> |
! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X2 = a a®b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
перетворю¹ться в слово |
|
|
|
|
|
|
|
. Далi за першою пiдстановкою отриму¹мо слово |
||||||||||||||||||||||||||||||
X |
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
= a ab b® |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
X4 = a b ab®, звiдки за заключною сьомою пiдстановкою остаточно ма¹мо слово X5 =
a b ab. Îòæå, A6(X) = X5.
4. Принцип нормалiзацi¨ поляга¹ в тому, що для довiльного конструктивно заданого алгоритму в деякому алфавiтi A можна побудувати еквiвалентний йому нормальний
алгоритм Маркова в деякому алфавiтi, який ¹ розширенням алфавiту A.
Цей принцип пiдтверджу¹ться експериментально. Впевненiсть в справедливостi принципу нормалiзацi¨ базу¹ться на всьому досвiдi людства у створеннi алгоритмiв, оскiльки серед рiзноманiтних алгоритмiв, якi створенi в наш час, нема¹ таких, якi не можуть бути нормалiзованi. Принцип нормалiзацi¨ можна сформулювати i так: кожний алгоритм нормалiзований.
5. Побудова нормальних алгоритмiв. Тепер ми розглянемо деякi операцi¨, якi можна виконувати над алгоритмами, що дають змогу за допомогою одних алгоритмiв будувати iншi.
5.1. Композицiя алгоритмiв. Послiдовне застосування до даного слова X двох алгоритмiв спочатку B, а потiм А назива¹ться композицi¹ю цих алгоритмiв i познача¹ться: D(X) = A(B(X)), тобто D = AB. Побудова узагальненого алгоритму
D, який ¹ композицi¹ю двох узагальнених нормальних алгоритмiв À i Â, викону¹ться
просто. Необхiдно вихiдний вузол граф-схеми алгоритму Â з'¹днати з вхiдним вузлом граф-схеми алгоритму А.
5.2. Об'¹днання алгоритмiв. Алгоритм D називають об'¹днанням алгоритмiв À i
Â, якщо вiн кожне слово X перетворю¹ в об'¹днання слiв A(X) i B(X), тобто
D(X) = A(X)B(X):
Для побудови граф-схеми об'¹днання алгоритмiв А i В треба переписати пiдстановки алгоритму А в алфавiтi двiйникiв i використати алгоритм A6 подво¹ння слiв.
Заключною частиною алгоритму D ¹ алгоритм A7 переходу вiд лiтер двiйникiв до вiдповiдних лiтер даного алфавiту (вважа¹мо, що A = fa; bg):
½ a ! a ; A7: b ! b :
75
Îòæå, D = A7ABA6, äå A означа¹ алгоритм A в алфавiтi двiйникiв.
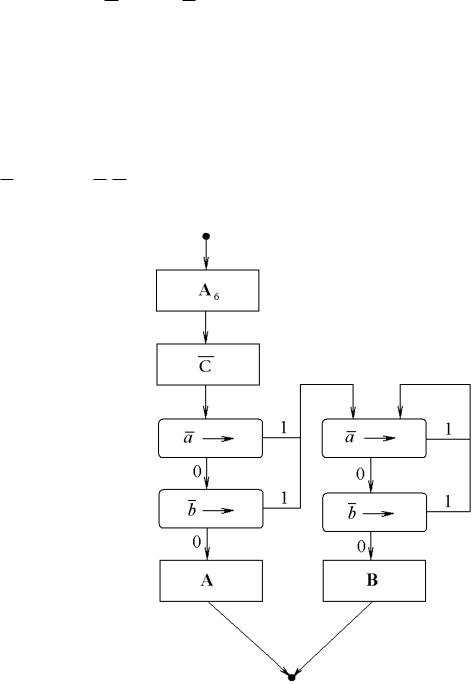
5.3. Розгалуження алгоритмiв. Алгоритм D називають розгалуженням двох даних алгоритмiв À i Â, який керу¹ться третiм алгоритмом C, якщо для довiльного слова
X в даному алфавiтi A ма¹мо спiввiдношення:
D(X) = ½ A(X); ÿêùî C(X) = ¤; B(X); ÿêùî C(X) 6= ¤;
äå ¤ означа¹ порожн¹ слово. Для побудови алгоритму D скориста¹мося алгоритмом
A6 подво¹ння слiв i перепишемо пiдстановки алгоритму C в алфавiтi двiйникiв, тодi C(A6(X)) = C(X)X для довiльного слова X. Граф-схема розгалуження двох алгоритмiв À i Â, який керу¹ться алгоритмом C, ма¹ такий вид:
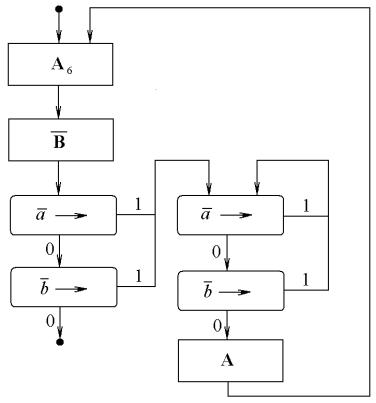
5.4. Iтерацiя алгоритмiв. Багаторазове повторення даного алгоритму À, яке керу¹ться алгоритмом Â, так що для довiльного вхiдного слова Х iсну¹ послiдовнiсть
ñëiâ X = X0; X1; X2; : : : ; Xn (n > 0), äëÿ ÿêî¨
Xk+1 = A(Xk) B(Xk) 6= ¤ B(Xn) = ¤;
ïðè
ïðè
0 6 k 6 n ¡ 1;
0 6 k 6 n ¡ 1;
назива¹ться iтерацi¹ю алгоритму A, яка керу¹ться алгоритмом B. Граф-схема iтерацi¨ ма¹ такий вигляд:
76
6.Поняття про унiверсальний алгоритм. Нехай A ¹ деякий нормальний алгоритм
âалфавiтi A. Покажемо, що цей алгоритм зображу¹ться в алфавiтi B = A[f®; ¯; °g, äå f®; ¯; °g \ A = ?, одним словом. Для цього послiдовно пiдстановки даного алгоритму виписуються так, що стрiлки замiнюються лiтерою ®, крапка лiтерою ¯, а слова пiдстановки роздiляються за допомогою °. Побудоване слово в алфавiтi B назива¹ться зображенням Au алгоритму A. Наприклад, розглянемо алгоритм
8
< ab ! a; A: aa !¢ b;
:ba ! a
âалфавiтi A = fa; bg. Тодi зображенням Au цього алгоритму ¹ слово:
ab®a°aa®¯b°ba®a:
Введемо нову лiтеру ±, тодi в алфавiтi B0 = B [ f±g буду¹мо зображення нормального алгоритму A i вхiдного слова X словом Au±X. Ма¹ мiсце наступна теорема, яку ми
формулю¹мо без доведення:
Теорема. Iсну¹ такий нормальний алгоритм N, який назива¹ться унiверсальним нормальним алгоритмом, що для довiльного алгоритму A i довiльного вхiдного слова X в алфавiтi A перетворю¹ слово Au±X в алфавiтi A[f®; ¯; °; ±g в слово A(X), тобто
N(Au±X) = A(X).
З цi¹¨ теореми виплива¹ принципова можливiсть побудови тако¨ машини, яка може виконувати роботу довiльного нормального алгоритму.
77
5.3 Про алгоритмiчно нерозв'язнi проблеми
Асоцiативне числення слiв. Проблема еквiвалентностi слiв. Приклади. Поняття про алгоритмiчно нерозв'язнi проблеми.
1. Асоцiативне числення слiв. В асоцiативному численнi слiв вводяться допустимi операцi¨ пiдстановок без будь-яких обмежень на порядок ¨х застосування. Якщо A
деякий алфавiт, а A i B слова в ньому, то неорi¹нтована пiдстановка позначатиметься через A $ B. Наприклад, пiдстановка ab $ bcb у двоелементному алфавiтi A = fa; bg може бути застосована до слова abcbcbab в рiзному порядку, тобто можна в цьому словi видiляти (причому не обов'язково злiва) або слово ab, або слово bcb, тобто abcbcbab, àáî
abcbcbab, àáî abcbcbab, àáî abcbcbab.
Означення 9. Асоцiативним численням назива¹ться сукупнiсть всiх слiв в даному абстрактному алфавiтi разом з деякою скiнченною системою допустимих пiдстановок. Асоцiативне числення зада¹ться алфавiтом i системою допустимих пiдстановок.
Якщо слово A ¹ результат одного застосування допустимо¨ пiдстановки до слова B, то, очевидно, що слово B також ¹ результатом застосування цi¹¨ ж пiдстановки до слова
A; такi два слова називаються сумiжними словами. Послiдовнiсть слiв A1; A2; : : : ; An, â
якiй два сусiднi слова ¹ сумiжними, назива¹ться дедуктивним ланцюгом, який з'¹дну¹ слова A1 i An. Два слова A i B називаються еквiвалентними (познача¹ться через A '
B), якщо iсну¹ дедуктивний ланцюг, який з'¹дну¹ цi слова. Ясно, що ' ¹ вiдношення
еквiвалентностi.
2. Проблема еквiвалентностi слiв поляга¹ в тому, що для довiльних двох слiв даного асоцiативного числення необхiдно визначити чи еквiвалентнi вони, чи нi. Ця проблема ма¹ важливе теоретичне i практичне значення в математицi.
Приклад 1. Асоцiативне допустимих пiдстановок
числення зада¹ться алфавiтом fa; b; cg i системою
ab $ ba; ac $ ca; bc $ cb:
Розглянемо нормальний алгоритм:
8
< ba ! ab;
A2: : ca ! ac; cb ! bc:
Результат застосування цього нормального алгоритму до довiльного слова X в алфавiтi fa; b; cg ¹ слово, у якого ¹ всi лiтери слова X, але вони упорядкованi так, що спочатку йдуть всi лiтери "a ", çà íèìè âñi ëiòåðè "b ", i ïîòiì "c ". Наприклад,
A2(bacbaca) = aaabbcc:
Алгоритм A2 перетворю¹ еквiвалентнi слова в даному асоцiативному численнi в рiвнi слова.
78
Приклад 2. Асоцiативне допустимих пiдстановок
числення зада¹ться алфавiтом fa; b; cg i системою
b $ acc; ca $ accc; aa $ ¤; cccc $ ¤:
Розглянемо нормальний алгоритм:
A3:
8
> b ! acc;
>
< ca ! accc;
>> aa ! ¤; : cccc ! ¤:
Слова в даному алфавiтi, якi можна отримати застосуванням алгоритму A3 äî ñëiâ
в цьому ж алфавiтi, назвемо зведеними словами. Покажемо, що зведеними словами в даному алфавiтi можуть бути лише слова:
¤; c; cc; ccc; a; ac; acc; accc:
Дiйсно, алгоритм A3 знищу¹ лiтери "b " в словах даного алфавiту; лiтера "a " завжди входить перед лiтерою "c " у зведених словах, причому не бiльше одного разу; лiтер
"c ", нарештi, не може бути бiльше трьох.
Покажемо далi, що довiльнi два зведених слова не еквiвалентнi мiж собою. Зразу ж вiдмiтимо, що при побудовi дедуктивного ланцюга можна не користуватись першою пiдстановкою. Справдi, якщо в кожному словi дедуктивного ланцюга замiнити лiтери "b " на слово acc, то отрима¹мо послiдовнiсть слiв, у якiй всi сусiднi слова або сумiжнi,
або просто рiвнi.
Оскiльки друга, третя i четверта пiдстановки не змiнюють парностi лiтер "a " i "c ", то жодне з перших чотирьох слiв, в якi лiтера "a " не входить, не еквiвалентне жодному
з чотирьох слiв, що залишаються, в якi входить лiтера "a " (непарне число разiв). Залиша¹ться тепер переконатися в нееквiвалентностi наступних пар слiв:
"¤" i "cc "; "c " i "ccc "; "a " i "acc "; "ac " i "accc ":
Неважко бачити, що з еквiвалентностi хоча б однi¹¨ пари виплива¹ еквiвалентнiсть iнших пар слiв, в чому легко переконатися.
Iндексом входження лiтери "a " в слово X назива¹ться число всiх входжень лiтери "c ", якi зустрiчаються правiше лiтери "a ". Iндексом слова X назива¹ться сума iндексiв всiх входжень лiтери "a ". Наприклад, в словi "accac " перша злiва лiтера "a " ìà¹
iндекс 3, друга 1, iндекс слова 4
Покажемо, що слова "a " i "acc " не еквiвалентнi. Iндекси цих слiв однаково¨ парностi (0 i 2). Пiдстановки aa $ ¤ i cccc $ ¤ не змiнюють парностi iндексу слова. Пiдстановка
æ AcaB i
AacccB. Iндекси входжень "a " â ñëîâi A змiню¹ться на 2; iндекси входжень "a " â ñëîâi B не змiню¹ться; iндекс входження "a " мiж словами A i B çìiíþ¹òüñÿ íà 3. Îòæå, â
цiлому iндекс слова змiню¹ться на непарне число.
Припустимо вiд супротивного, що слова "a " i "acc " еквiвалентнi, тобто iсну¹ дедуктивний ланцюг, який зв'язу¹ цi слова; ланцюг побудований за допомогою
79
пiдстановок: ca $ accc; aa $ ¤; cccc $ ¤. Оскiльки пiдстановка cccc $ ¤ змiню¹ число входжень лiтери "c " на 4, а пiдстановка aa $ ¤ зовсiм не змiню¹ числа входжень "c ", то для побудови дедуктивного ланцюга, яка зв'язу¹ "a " i "acc ", необхiдно застосувати
пiдстановку ca $ accc, причому непарне число разiв. Але при цьому iндекс слова
змiню¹ться на непарне число, що протирiччить однаковiй парностi iндексiв цих слiв. Отже, слова "a " i "acc " не еквiвалентнi.
3. Поняття про алгоритмiчно нерозв'язнi проблеми. Iснування алгоритмiчно нерозв'язних проблем можна сформулювати так: iснують такi класи задач, для яких не iсну¹ ¹диного нормального алгоритму ¨х розв'язання. Наприклад, росiйський математик П. С. Новiков вперше встановив алгоритмiчну нерозв'язнiсть проблеми тотожностi в теорi¨ груп. Ще одним прикладом нерозв'язно¨ проблеми в теорi¨ алгоритмiв ¹ проблема розпiзнання самозастосовностi алгоритмiв.
Пояснимо в чому поляга¹ ця проблема. Розгляда¹мо нормальнi алгоритми в алфавiтi A, який склада¹ться с двох лiтер. Нехай Au ¹ слово в алфавiтi A, ÿêå
зображу¹ алгоритм A.кщо алгоритм A застосовний до слова Au, òî A назива¹ться
самозастосовним, iнакше вiн назива¹ться несамозастосовним. Iснують алгоритми обох видiв. Наприклад, тотожнiй алгоритм A1(X) = X самозастосовний, а алгоритм
Aa(X) = aX приписування лiтери несамозастосовний.
Проблема розпiзнавання самозастосовностi алгоритмiв поляга¹ в тому, щоб знайти ¹диний алгоритм, який би за схемою довiльного нормального алгоритму A
встановив, чи самозастосовний алгоритм A, ÷è íi.
Згiдно принципу нормалiзацi¨ цю задачу достатньо розглядати лише для нормальних алгоритмiв. Iснування алгоритмiчно нерозв'язних проблем означа¹, що при вiдшуканнi алгоритму, який розв'язу¹ ту чи iншу проблему, потрiбно мати на увазi, що такий алгоритм може взагалi i не iснувати. Тому разом зi спробами побудови алгоритму треба намагатися також довести його iснування.
80
