Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Днепропетровский национальный университет им. Олеся Гончара

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1211021

.pdf

Скачиваний:

Добавлен:

23.03.2015

Размер:

751.07 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 63 4 5 6 > Следующая >>>

Продолжение

таблицы 3.1

11.

x > 1.5

2 x 2

cos( 2 x)

0 ≤ x ≤ 1.5

[-1; 3]

0.5

y =

−cos( 3 x )

x < 0

12.

1 −

cos( 2 x)

x > 2.5

− x

1 ≤ x ≤ 2.5

[0; 3]

0.3

y = x 2

1 + x 2

x < 1

13.

x > 4.5

y =

1−ln

1− x2

0 ≤ x ≤ 4.5

[-0.5; 5]

0.5

−x

x < 0

14.

ln(x2 −1)

x > 2

y =

−2x3

≤

[-π/2; π]

π /5

sin(x)

x < 0

15.

−

2x3

x > 3.5

− x

y =

cos(2x −1)

0 ≤ x ≤3.5

[-0.5; 4.5]

0.25

e−cos(2x)

x < 0

16.

x +1

x > 2.5

y =

1− x5

0 ≤ x ≤ 2.5

[-π; 2π]

π /5

x +ln

sin(x)

x < 0

17.

x −2

x > 2.5

y =

1 + x2

0 ≤ x ≤ 2.5

[-π/2; 2π]

π /4

x ln

cos(x)

x < 0

18.

1+3x

x > 4.5

y =

−2x

1 ≤ x ≤4.5

[-π/2; 2π]

π /5

x < 1

cos(2x)

19.

tg (x 2

−1)

x > 4

y =

0 ≤ x ≤ 4

[-2; 5]

0.5

− 2x

cos( x)

x < 0

Окончание

таблицы 3.1

20.

x > 1

e ( x + 2 )

-1≤ x ≤ 1

[0.8; 2.5]

0.1

1 - 2 x

2 x

− 3

−

x < -1

21.

− x

x > 2

− 2 x

0 ≤ x ≤ 2

[-1; 2.5]

0.25

y =

cos( x )

x < 0

22.

tg ( x) −1

x < -3.14

1 +

y =

-3.14≤x ≤3.14

[-9π/5; 9π/5]

π /5

1 + x

x > 3.14

23.

x > 4.5

x 3 )

ln(

2 x + 0 .1

0 ≤ x ≤ 4.5

[-0.5; 5]

0.25

x < 0

24.

−

3 +

2.5x

x > 2

y =

e( x) +5 +cos(0.001x)

-1≤ x ≤ 2

[-2.5; 2.5]

0.5

tg(2x)

−1

x < -1

25.

cos (2.3 x − 1)

x > 5.5

− 3 ln (1 + x )

0 ≤x ≤ 5.5

[-1; 8]

0.5

= 1

x < 0

− x

Лабораторная работа № 4

Табулирование функции и ее разложения в сумму ряда

Задание: Составить блок-схему и программу табулирования двух функций S и Y в заданном диапазоне изменения аргумента x. Здесь n - число слагаемых суммы S.

Результат табулирования вывести в форме следующей таблицы:

------------------------------------------------------------------

! X ! y = f(x) ! S !

------------------------------------------------------------------

Теоретический материал

Выполнение данной лабораторной работы потребует использования, как и в предыдущей работе, операторов цикла. Однако здесь будет использовано два циклических оператора, причем один окажется вложенным в другой, т. е. тело внешнего цикла будет содержать еще один оператор цикла. При этом следует внимательно следить за количеством операторов, составляющих тело цикла (за исключением цикла repeat .. until). В случае если количество операторов тела цикла больше одного, все операторы, которые необходимо выполнить в цикле, заключаются в операторные скобки (begin..end).

Пример выполнения лабораторной работы

Для примера рассмотрим функцию у= 3x , разложенную в							сумме ряда
s=1+	ln 3	x +	ln2 3	x2	+K	(количество слагаемых n=10). В задаче	необходимо
			2!
1!

протабулировать эти функции на интервале изменения x [0,1; 1]. Заметим, что значения s и y при одинаковых значениях x будут приблизительно равными.

Примечание: k! – факториал числа k. Вычисляется по формуле

k! = 1*2*3*…*k

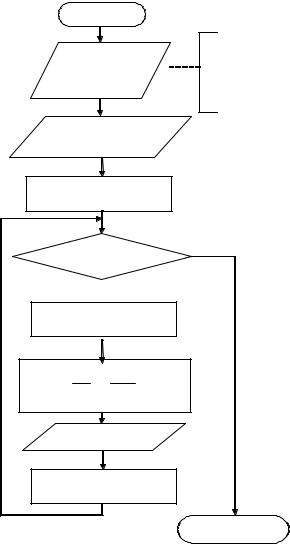
Прежде чем приступать к решению данной задачи, составим общую блок-схему алгоритма (рис. 4.1).

Данная блок-схема дает общее представление об алгоритме вычислений, однако, требуется более детальное описание действий по алгоритму вычисления суммы ряда. Для этого необходимо, прежде всего, найти закономерность вычисления каждого слагаемого ряда. В данном случае эта закономерность определяется формулой

(ln 3 ) i	x i ,	(1)
i!

где i – номер слагаемого (в данном случае изменяется от 0 до 10).

По этой формуле получается, что

(ln 3 ) 0 x 0

0-е слагаемое равно 0! .

	начало
	Вывод	Автор, номер
	Вывод	варианта,
информац.		варианта,
информац.		назначение
	блока	назначение
	блока	программы
		программы
	Вывод
‘X	Y	S’
	x= 0,1

x<= 1	нет

да

y=3x

s=1+ ln3 x +ln2 3 x2 +K 1! 2!

Выводx, y, s

x= x+ 0,05

конец

Рис. 4.1. Общая блок-схемазадачи табулирования функций

Любое число в степени 0 дает 1, факториал числа 0 также равен 1. Получается нулевое слагаемое рано 1.

Первое слагаемое будет равно	(ln 3 ) 1	x 1	и т. д. Последовательно вы-
	1!

числяя и суммируя все слагаемые при определенном значении x, получим требуемую сумму. Для этого организуем цикл, повторяющийся n+1 раз (включая нулевое слагаемое), на каждой итерации которого будет вычисляться значение очередного слагаемого и прибавляться к накапливаемой сумме s (рис. 4.2).

начало

Вывод информац. блока

Вывод

‘X Y S’

x= 0

x<= π нет

да

y=3x; s=0

i от0 доn шаг1

s=s+ (ln 3)i x i i!

Выводx, y,s

x= x+ 0,05

конец Рис. 4.2. Блок-схемазадачитабулированияфункций

Данный алгоритм является приемлемым, если язык программирования, на котором он будет реализован имеет стандартные процедуры и функции для всех математических операций, используемых в данном алгоритме. Однако Паскаль не располагает встроенными функциями ни для вычисления степени числа (за исключением квадрата), ни для вычисления факториала. Поэтому требуется программировать и эти алгоритмы вычислений. В нашем случае это можно сделать с помощью еще одного вложенного цикла, в котором вычисляется и степень числа и его факториал (рис. 4.3, а), либо только факториал, а для вычисления

степени	используется	математи-
ческая формула (2) (рис. 4.3, б).
	xn=en*lnx	(2)
В	языке Паскаль	имеются

стандартные функции и для вычисления натурального логарифма Ln(x), и для вычисления экс-

поненты exp(ln(x)).

начало

Вывод информац.

блока

Вывод

‘X Y S’

x= 0

x<= π		нет
x<= π
	да


y=3x; s=0

i от 0 до n шаг 1
i от 0 до n шаг 1



step_x=1;
step_ln=1;fact=1

j от 1 до i шаг 1

step_x= x *step_x

step_ln= ln(x) *step_ln

fact= fact*j

s=s+step_ln/fact*step_x

Вывод x, y,s

x= x+ 0,05

конец

начало

Вывод информац.

блока

Вывод

‘X Y S’

x= 0

x<= π		нет
x<= π
	да
	да

y=3x; s=0

i от 0 до n шаг 1
i от 0 до n шаг 1



step_x= ln(i*ex)

step_ln= ei*ln(x)

fact=1

j от 1 до i шаг 1

fact= fact*j

s=s+step_ln/fact*step_x

Вывод x, y,s

x= x+ 0,05

конец

а б

Рис. 4.3. Блок-схема алгоритма вычисления значений функций

Недостатком таких алгоритмов является организация дополнительного цикла, в котором вычисление степеней и факториала начинается с самого начала. Устраняет этот недостаток алгоритм, представленный в виде блок-схемы на рис. 4.4.

начало

Вывод информац.

блока

Вывод

‘X Y S’

x= 0
x<= π	нет
x<= π

да

y=3x

s=1; slag=1

i от 1 до n шаг 1

slag= slag*ln(3)/i*x

s=s+slag

Вывод x, y,s

x= x+ 0,05

конец Рис. 4.4. Блок-схема задачи табулирования функций

В нем учитывается, что каждое последующее слагаемое можно выразить через предыдущее следующей формулой:

slag	i = slag	i −1	(ln	3 )	x	,
				i

где i – номер слагаемого, причем нулевое слагаемое равно 1.

Действительно,

slag

(ln

3 ) 1

x 1 ,

slag

(ln

3 ) 2

x 2 =

(ln 3 ) 1

x 1 *

ln 3

x = slag

ln 3

Итак, приступим к программной реализации данного алгоритма.

В программе потребуются переменные x, y, s, slag вещественного типа real, а также переменная i целочисленного типа byte. Кроме того, можно задать как константу количество слагаемых n и шаг изменения аргумента функции x.

program lab4; const n=10;

h=0.05; var i:byte;

x,y,s,slag:real;

Текст информационного блока, с которого начинается тело программы, подробно рассматривать не будем. Перейдем сразу к формированию шапки таблицы и заданию начального значения x.

writeln (’!	x	!	y	!	s	!’);
x:=0;

Теперь организуем «внешний» цикл, в котором будут изменяться значения аргумента x до тех пор, пока не будет достигнута верхняя граница заданного интервала [0,1; 1]. У компилятора Turbo Pascal имеется некоторая особенность работы с данными вещественного типа: из-за небольших погрешностей вычислений переменная х в конце цикла может принять значение чуть меньше единицы, поэтому условие x<=1 может оказаться ложным, хотя по нашим подсчетам должно быть истинным. Для того, чтобы избежать такой ситуации, в качестве условия выхода из цикла можно использовать выражение x<1+h.

Тело цикла содержит несколько операторов, поэтому необходимо использовать операторные скобки. В теле «внешнего» цикла будет находиться еще один цикл, вычисляющий очередное слагаемое и постепенно формирующий сумму из n слагаемых. Заранее известное количество повторений (количество слагаемых равно 10) делает целесообразным использование оператора цикла for, в котором параметром цикла будет номер слагаемого.

while x<1+h do begin

y:=exp(x*ln(3)); s:=1; slag:=1; for i:=1 to n do begin

slag:= slag*ln(3)/i*x;

s:=s+slag;

end;

writeln(’!’,x:7:2,’ !’,y:7:3,’ !’,s:7:3,’ !’); x:=x+h;

end;

Далее остается лишь написать пустой оператор ввода readln для задержки результатов на экране.

readln;

end.

Ниже представлен полный текст программы.

program lab4;
const n=10;
h=0.05;
var i:byte;
x,y,s,slag:real;
Begin
writeln;
writeln(’	Автор – Иванов И.П., студент гр. ИСЭд-11’);
writeln(’	Вариант № 100’);
writeln(’ Программа табулирования функции y=3^x, а также суммы
ряда ’);
writeln(’	ln(x)		ln(x)^2			ln(x)^n ’);
writeln(’s= 1 + -----x + -------x^2 + ... +--------x^n’);
writeln(’	1!		2!			n!’);
writeln(’на отрезке [0.1;1] с шагом 0.05’);
writeln;
writeln (’!	x	!	y	!	s	!’);
x:=0;
while x<1+h do
begin
y:=exp(x*ln(3));
s:=1;	{Начальное значение суммы, включая нулевое слагаемое}
slag:=1; {Значение нулевого слагаемого}
for i:=1 to n do
begin
slag:= slagln(3)/ix;
s:=s+slag;
end;
writeln(’!’,x:7:2,’			!’,y:7:3,’		!’,s:7:3,’		!’);
x:=x+h;
end;

readln;

end.

Таблица 4.1

Варианты заданий

Диапазон

Сумма S

изменения

Функция Y

вар.

1 +

[1;2 ]

cos x + cos 2x

+ cos3x

[-π/5; 9π/5]

−ln

2sin

x −

−K

[0,1; 1]

sin x

sin x − sin 2x + sin 3x −K

[-π/5; 4π/5]

cos x +

cos 3x

cos 5x

[π/5; π]

π2

− 4

cos π

cos 2 π

[0,1; 1]

x cosπ

x +

4 cos(x sin

4 )

[0,1; 1]

cos x

1− 2! + 4! −K

x sin

+ x

sin 2

[0,1; 0,8]

1−

2x cos

+ x

x13

[0,1; 0,8]

1 + x 1

x +

arctgx

1 − x

cos x

cos 2x

[0,1; 1]

ecos x cos(sin x)

3x2

5x4

[0,1; 1]

(1+2x2 ) ex2

x cos

x2 cos 2

−

+ x

)

[0,1; 0,8]

2 ln(1−2x cos 3

Окончание таблицы 4.1

x −1

−

1 3

−

1 5

[0,2; 1]

ln x

x +1

−cos x +

cos 2x

−

cos3x

[-π/5; π]

(

−

π 2

)

−

−K

[0,1; 1]

1 + x2

arctgx −

sin x + sin 3x + sin 5x +K

[π/10; 9π/10]

[0,1; 1]

e x

+e−x

cos 2x

cos 4x

cos6x

[0,1; 0,8]

1 −

sin x

(2x)2

[0,1; 1]

2 x

5 x

[0,1; 1]

+1 e

2! 2

[0,1; 0,5]

arctgx

x − 3 + 5 − 7 +K

3 2

5 4

10 6

sin x

1 −

−

x +K

[0,1; 1]

−

cos x −

−

(2x)2

(2x)4

−

(2x)6

[0,1; 1]

2cos2 x −1

−(1+ x)2

(1+ x)

−

(1+ x)

[-0,2; -0,1]

2 + 2x + x

x +

[0,1; 1]

e x

−e−x

<<< < Предыдущая 1 23 / 63 4 5 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
20.11.201954.98 Кб211.docx
#
21.11.201930.89 Кб311.Оператор SELECT языка SQL назначение, синтак...docx
#
15.09.20199.61 Mб11119___2.doc
#
01.04.2025117.76 Кб012 ОЕН МВК КР 11.doc
#
20.11.201930.27 Кб512.docx
#
23.03.2015751.07 Кб131211021.pdf
#
01.05.2025452.01 Кб0126469.rtf
#
22.11.2019328.95 Кб6128693.rtf
#
01.04.20252.87 Mб013 лекція.doc
#
23.03.201578.71 Кб613.docx
#
13.11.201923.05 Кб213.Орієнтовні тести до заліку МВВШ.docx