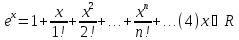- •2. Неперервність ф-ї багатьох змінних.
- •3. Частинні похідні. Диференціал функцій багатьох змінних.
- •4. Повний диференціал функції багатьох змінних. Диференціали вищих порядків.
- •5. Похідні складної ф-ї багатьох змінних. Диференціал складної ф-ї багатьох змінних.
- •6. Екстремум ф-ї 2 змінних. Необхідні і достатні умови.
- •7. Невласні інтеграли 1 роду. Приклади.
- •8. Невласні інтеграли 2-го роду.
- •9.Числові ряди. Найпростіші властивості.
- •10.Достатні ознаки збіжності додатних числових рядів. Приклади. А).Ознаки порівняння додатніх числових рядів.Приклади.
- •11. Знакопочередні ряди. Ознака Лейбніца. Знакозмінні ряди. Абсолютна і умовна збіжності.
- •12.Функціональні ряди. Поняття рівномірної збіжності. Ознака Вейєрштраса
- •13. Степеневі ряди
- •14. Ряд Тейлора
- •15. Тригонометрический ряд Фур’є
- •16. Подвійний інтеграл умови його існування і властивості.
14. Ряд Тейлора
Нехай
f(x)
є
сумою
степ. ряду
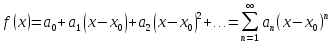 (1) на (-R,
R).
Вираз
(1) наз. також розкладанням ф-ції f(x) в
околі точки
(1) на (-R,
R).
Вираз
(1) наз. також розкладанням ф-ції f(x) в
околі точки
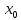 або розкладання ф-ції
за
степенями
або розкладання ф-ції
за
степенями
 .
Числа
.
Числа
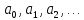 наз. коефіціентами цього розкладую
Задача полягає в тому щоб у дифірінціальному
ряді (1) знайти коефіцієнти розкладання.
За властивістю степеневих рядів, ряд
(1) можна дифірінціювати скільки завгодно
раз і одержані в результаті цього ряди
будуть мати інтервали збіжності
наз. коефіціентами цього розкладую
Задача полягає в тому щоб у дифірінціальному
ряді (1) знайти коефіцієнти розкладання.
За властивістю степеневих рядів, ряд
(1) можна дифірінціювати скільки завгодно
раз і одержані в результаті цього ряди
будуть мати інтервали збіжності
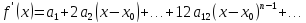
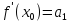



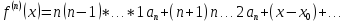

Звідси
одержимо
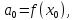
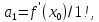 … ,
… ,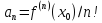
Підставляючи
знайдені коефіцієнти в (1) одержимо
степеневий ряд
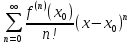 (2).
(2).
Опр. Ряд (2) наз. рядом Тейлора ф-ції f(x).
Теорема
1:
Якщо
ф-ція
f(x)
на
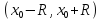 подана у вигляді
степ. Ряду
(1),
то це
подання єдине і
даний
степ. ряд є рядом
Тейлора ф-ції
f(x).
подана у вигляді
степ. Ряду
(1),
то це
подання єдине і
даний
степ. ряд є рядом
Тейлора ф-ції
f(x).
Виявляється,
що у випадку коли ф-ція f(x)
нескінченно
раз дифірінційовна на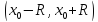 ,
її ряд Тейлора (2) зовсім не обов’язково
буде збігатися до ф-ції f(x), для якої він
формально був не будований.
Цей ряд (2) взагалі може збігатися зовсім
до іншої ф-ції. Виникає питання: за яких
умов ряд Тейлора (2) ф-ції f(x) збігається
саме до f(x) існує декілька тверджень в
яких розглядаються такі умови. На
практиці частіше користуються наступною
теоремою.
,
її ряд Тейлора (2) зовсім не обов’язково
буде збігатися до ф-ції f(x), для якої він
формально був не будований.
Цей ряд (2) взагалі може збігатися зовсім
до іншої ф-ції. Виникає питання: за яких
умов ряд Тейлора (2) ф-ції f(x) збігається
саме до f(x) існує декілька тверджень в
яких розглядаються такі умови. На
практиці частіше користуються наступною
теоремою.
Теорема
2
Нехай ф-ція
f(x)
має похідну будь-якого порядку на
 і
і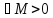 таке що n=0,1,2,3..
і
таке що n=0,1,2,3..
і
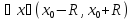 виконується нерівність
виконується нерівність
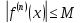 .
.
Озн.
Рядом
Маклорена наз. ряд Тейлора (2), якщо
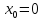 :
:
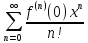
Розглянемо далі розкладення в ряд (3) деяких елементарних ф-цій:
Для
доведення
формули (4) розглянемо
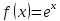 ,
,
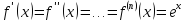 ,
,
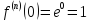 тоді
за формулою (2) ряд Тейлора
ф-ції
тоді
за формулою (2) ряд Тейлора
ф-ції
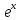 має вигляд
має вигляд
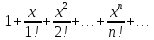 знайдемо його радіус збіжності
знайдемо його радіус збіжності тобто даний степеневий ряд збігається
на всій числовій осі. Покажемо,
що він збігається саме до
тобто даний степеневий ряд збігається
на всій числовій осі. Покажемо,
що він збігається саме до
 .
Розглянемо будь-яий інтервал
.
Розглянемо будь-яий інтервал
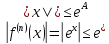 .
Оскільки
А будь-яке додатне число, то за теоремою2
побудований степеневий ряд збігається
до ф-ції
.
Оскільки
А будь-яке додатне число, то за теоремою2
побудований степеневий ряд збігається
до ф-ції
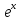 .
.
Розглянемо
 ,
,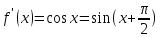 ,
,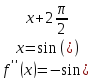 ,
, ,
тоді
,
тоді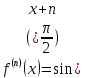 .
.
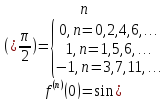
Враховуючи
це за формулою (3) одержимо ряд
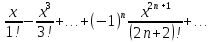 .
Знайдемо радіус збіжності
.
Знайдемо радіус збіжності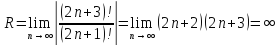 тобто даний степеневий ряд збігається
во всіх точках дійсної осі його збіжності
саме до ф-ції sin(x) випливає із теореми2
і до того факту що
тобто даний степеневий ряд збігається
во всіх точках дійсної осі його збіжності
саме до ф-ції sin(x) випливає із теореми2
і до того факту що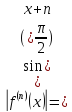 .
.
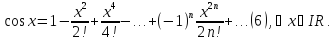 Формулу
(6) можна довести так
само як і формулу (5), але це можна зробити
значно простіше. Продифірінціювавши
почлено степеневий ряд (5).
Формулу
(6) можна довести так
само як і формулу (5), але це можна зробити
значно простіше. Продифірінціювавши
почлено степеневий ряд (5). (7)
(7)
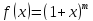 ,
,
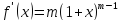 ,
,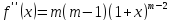 ,…,
,…,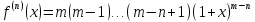 тоді
тоді
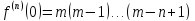 .
.
Підставляючи
це
у формулу (3) одержимо ряд Маклорена
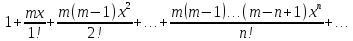 Знайдемо радіус сбіжності одержаного
степеневого ряду
Знайдемо радіус сбіжності одержаного
степеневого ряду
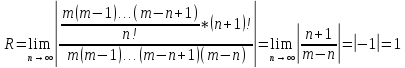 тобто даний ряд збігається на інтервалі
(-R,R),
того факту що цей ряд збігається саме
до ф-ції
тобто даний ряд збігається на інтервалі
(-R,R),
того факту що цей ряд збігається саме
до ф-ції
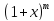 не наводимо. Якщо
не наводимо. Якщо
 ряд (7) наз. біноміальним. На практиці
зустрічаються частині випадки формули
(7), якщо m= - 1:
ряд (7) наз. біноміальним. На практиці
зустрічаються частині випадки формули
(7), якщо m= - 1:
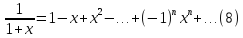 .Якщо
у формулі (8) замість Х взяти -Х одержимо
ряд
.Якщо
у формулі (8) замість Х взяти -Х одержимо
ряд
 Якщо
крім того у формулі (8) почленно про
інтегрувати степеневий ряд одержимо
вираз
Якщо
крім того у формулі (8) почленно про
інтегрувати степеневий ряд одержимо
вираз
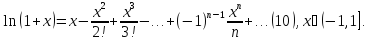
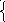
15. Тригонометрический ряд Фур’є
Озн:Тригонометричним
рядом на
в
[-π,π],
наз. функціональний ряд вигляду
 (1),
де а0,а1,...,b1,b2,…-
дійсні числа, які наз. коефіцієнтами
тригонометричного ряду.(1)
(1),
де а0,а1,...,b1,b2,…-
дійсні числа, які наз. коефіцієнтами
тригонометричного ряду.(1)
Нехай
f(x)
подана у вигляді рівномірнозбіжного
до неї триг. ряду(1)
 (2).
За власт-ми ряд(2)можна почленно
інтегрувати. проінтегр. на[-π,π]
(2).
За власт-ми ряд(2)можна почленно
інтегрувати. проінтегр. на[-π,π]
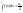

Звідси одержимо:
 ,
(3).
,
(3).
Помножимо тепер обидві частини рівності (2) на coskx і проінтегрувати одержаний вираз на відрізку [-π,π] одержимо:

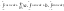 Звідси
одержимо
Звідси
одержимо
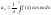
(4)
Аналогічно
помноживши (2) на sinkx
і проінтегрувавши одержаний вираз на
[-π,π],
одержимо:
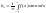 ,(5).
,(5).
Озн: Тригонометричний ряд (1) коеф. якого обчислені за формулами (3), (4), (5) наз. рядом Фур’є ф-ї f(x), а самі коеф-ти 3 і 4 наз. коеф. Фур’є.
Розглянемо задачу: нехай задана 2π- періодична ф-ція f(x). Побудуємо для цієї ф-ції ряд Фур’є
 (6),
де a0,an,bn
– визначається
відповідно за формулами (3), (4), (5)
(6),
де a0,an,bn
– визначається
відповідно за формулами (3), (4), (5)
Однак виявляється, що побудований формально ряд (6) взагалі кажучи зовсім не обов’язково буде збігатися до ф-ції f(x), а може збігатися до зовсім іншої ф-ції. Аналогічне явище спостерігалося раніше для рядів Тейлора. Розглянемо далі теорему в якій наведені умови за яких ряд Фур’є ф-ції f(x) збігається саме до ф-ції f(x).
Теорема 1 (б/д)
Якщо ф-ю f(x) можна подати у вигляді рівномірно збіжною тригоном. ряду (2) то це подання єдине і данний тригоном. ряд є рядом Фур’є цієї ф-ї.
Озн
Ф-цію f(x) наз. Кусково-монотонною на відрізку [a,b], якщо існує таке розбиття відрізка на n частин a=x0<x1<…<xn=n, що на кожн. з від-ку [xi-1; xi] ф-ція f(x) монотонною.

Теорема 2: Нехай f(x) обмежена, 2π- періодична і кузково-монотонна ф-я на всій осі, тоді ряд Фур’є ф-ї f(x) є збіжним на всій числовій осі і сума S(x) цього ряду дорівнює значенню ф-ї f(x), якщо х0-точка розриву ф-ї f(x), то
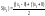 .
.
Зауваження: порівнюючи умови розкладання ф-ї у ряд Тейлора і ряд Фур’є можна побачити, що останній значно простіший. По-перше, ф-ція зовсім необов’язково повинна мати похідні будь-якого порядку і взагалі кажучи вона може бути розривною. Тому клас ф-ції яких можна подати рядом Фур’є значно ширше, тих що подаються рядом Тейлора. Крім того виявляється, що випудку, коли ф-ція f(x) є парною, або непарною задача знаходження коєфіц. Фур’є значно спрощ. Так для парної ф-ції f(x) ряд Фур’є містить лише косинуси.
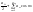
і коефіц. Фур’є обчислюємо:
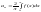 ,
,
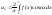 (7)
(7)
Для непарної ф-ції ряд Фур’є містить лише синуси
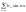
n=1,2,…
bn=2/π n=1,2,…
коеф.
n=1,2,…
коеф.
Це невипадково, оскільки таке подання відображає хар-тер ф-ції. Для парної ф-ції ряд Фур’є скл. З парних ф-цій косинусів, а для непарних – з непарних ф-цій синусів.
У вип., якщо ф-ція розгляд на відрізку [-1,1], зробивши в ф-лах (3), (4), (5) заміну змінної одержимо наступні ф-ли для коефіц. Фур’є такої ф-ції:

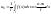
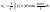 а
сам ряд Фур’є має вигляд:
а
сам ряд Фур’є має вигляд: