
- •2. Неперервність ф-ї багатьох змінних.
- •3. Частинні похідні. Диференціал функцій багатьох змінних.
- •4. Повний диференціал функції багатьох змінних. Диференціали вищих порядків.
- •5. Похідні складної ф-ї багатьох змінних. Диференціал складної ф-ї багатьох змінних.
- •6. Екстремум ф-ї 2 змінних. Необхідні і достатні умови.
- •7. Невласні інтеграли 1 роду. Приклади.
- •8. Невласні інтеграли 2-го роду.
- •9.Числові ряди. Найпростіші властивості.
- •10.Достатні ознаки збіжності додатних числових рядів. Приклади. А).Ознаки порівняння додатніх числових рядів.Приклади.
- •11. Знакопочередні ряди. Ознака Лейбніца. Знакозмінні ряди. Абсолютна і умовна збіжності.
- •12.Функціональні ряди. Поняття рівномірної збіжності. Ознака Вейєрштраса
- •13. Степеневі ряди
- •14. Ряд Тейлора
- •15. Тригонометрический ряд Фур’є
- •16. Подвійний інтеграл умови його існування і властивості.
8. Невласні інтеграли 2-го роду.
Нехай
ф-я f(x)
визначена на проміжку [a,b)
точку х=b
назвемо особливою точкою ф-ції f(x)
якщо lim
f(x)=
коли х
b->0.
Озн. Нехай f(x)
визначена на проміжку [a,b)
де точка b
- особлива і інтегровна на будь-якому
відрізку [a,b-
ε). Якщо існує границя
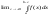
 то її наз. Невласним інтегралом 2-го
роду і позначають
то її наз. Невласним інтегралом 2-го
роду і позначають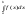 .
.
Тобто
за озн.
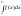 =
=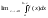 (1)
(1)
Якщо
границя в (1)існує і скінченна, ф-цію
f(x)
наз. інтегровною на проміжку[a;b],
а сам невласний інтеграл
 наз. збіжним. У випадку, якщо границя в
(1) не існує або нескінченна,то ф-ціюf(x)
наз. неінтегровною на [a;b]
а сам невласний інт-л наз-ся розбіжним.
наз. збіжним. У випадку, якщо границя в
(1) не існує або нескінченна,то ф-ціюf(x)
наз. неінтегровною на [a;b]
а сам невласний інт-л наз-ся розбіжним.
Аналогічно визнач. невласний інтеграл 2-го роду, якщо особливою є точка а.
 =
=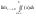 (2)У випадку якщо особливими є точки а
і в, невласний інтегр визнач.
(2)У випадку якщо особливими є точки а
і в, невласний інтегр визнач. =
=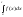 +
+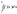 (3)
(3)
де с – довільна точка із інтервала [a;b]
Інтеграл (3) вважаєм збіжним якщо збігаються обидва інтеграла у правій частині (3) Можна довести, що інтаграл (3) не залежить від вибору внутрішньої точки с. У випадку якщо особливою точкою є внутрішня точка відрізка [a;b] невласний інтеграл 2-го роду визнач так
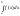 =
=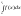 +
+
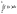
(4)
де т. с0 – особлива точка ф-ції f(x). Інтеграл (4) вважають збіжним, якщо збігаються обидва інтеграли у правій частині (4)
Як і невласні інтеграли 1-го роду не є границями інтегральних сум, а визнач. як інтеграли із змінними межами інтегрування. Геом. зміст інтегралів (1) – (4) полягає в тому, щоб вони визначали площу необмеженої поверхні
Деякі достатні ознаки збіжності невласних інтегралів 2-го роду. Сформулюємо для інтегралів виду (1). Для виду (2) –(4) формулюються аналогічно.
Теорема 1( ознака порівняння)
Нехай
ф-ції f(x)
і g(x)
додатні і неперервні на проміжку [a;b)
і b
– особлива точка 2-х ф-цій. Якщо для всіх
х що належать [a;b)
існує нерівність 0f(x)g(x)
від збіжності інтегралу
 випливає збіжність
випливає збіжність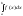 .
А із розбіжності
.
А із розбіжності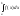 випливає розбіжність
випливає розбіжність .
Наведена теорема має такий геом. зміст:
.
Наведена теорема має такий геом. зміст:
Якщо площа більшої за розміром обл. є скінченне число, то площа меншої обл. також скінченна. У випадку, якщо площа меншої обл. нескінченна величина, то площа більшої обл. також нескінченна.
Теорема 2 (гранична ознака порівняння)
Нехай
ф-ції f(x)
і g(x)
неперервні додатні на проміжку [a;b)
і т. в- особлива точка обох ф-цій. Якщо
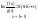 ,
то інтеграли
,
то інтеграли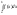 і
і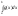 або одночасно збігаються, або одночасно
розбігаються.
або одночасно збігаються, або одночасно
розбігаються.
Наведені теореми 1 і 2 справедливі лише для додатніх ф-цій. Для знакозмінних ф-цій справедлива
Теорема
3:
Нехай f(x)
неперервна на проміжку [a;b),
т. в – особлива.Якщозбігаеться
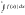 то збігається і інтеграл
то збігається і інтеграл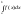 .
Твердження обернене до твердження
данної теореми неправильне. Із збіжності
.
Твердження обернене до твердження
данної теореми неправильне. Із збіжності не випливає збіжність
не випливає збіжність
Відрізняють випадки:умовно и абсол збижн.
9.Числові ряди. Найпростіші властивості.
Озн. : Нехай задана посл-ть дійсних чисел {an}∞n=1={a1,a2,…., an ….}.
Числовим
рядом наз-ся вираз a1,a2,….,
an
…=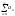 .(1)
.(1)
Цьому ми не приписуємо ніякого числа, тому що не можна виконати нескінченну суму.anназ. загальним членом ряду (1).
Частинною сумою ряду (1) наз. вираз Sn a1+a2+., +an
Сумою ряду (1) наз. S = lim Sn якщо ця границя існує.
n->∞
Ряд
1 наз. збіжним, якщо сума S
–скінченне число, тоді пишуть
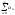 =S
=S
Якщо
ця границя є нескінченна або не існує
ряд 1 наз. розбіжним. Це позначають
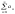 =
=
Приклади:
Геом. прогресія
∞
a + aq +…+ aqn-1+ …=∑ aqn-1 Sn= a + aq +…+ aqn-1 = a(1-q)/1-q= a/1-q - aqn/ 1-q = a/1-q, |q|<1
n=1 , |q|>1
У випадку, якщо q=1 Sn= a + a +...+а = na ->
n-> ряд розбіжний. Геом. прогресія збігаеться, якщо|q|<1 і розбігається якщо |q|≥1
2. Гармонічний ряд
∞
1+ 1/2 + 1/3+…+1/n+…=∑1/n Покажемо, що цей ряд розбіжний. При доведенні формули для числа е ми розглядали
n=1
послідовність {xn} ={(1 +1/n)n} Ми довели, що ця послідовність зростаюча і обмежена зверху числом е. Для будь-якого
n=1 n=1
nє|N (1+1/n)n <e
прологарифмуємо ln(1+1/n)n <lne
nln(1+n/n )<1
ln(1+n)-ln(n)<1/n (2)
Запишемо нерівність (2) для n=1,2,3…
ln2 – ln1<1
ln3 – ln2<1/2
ln4 – ln3<1/3 ln (n+1) – ln(n)< 1/n
Додамо відповідні ліві та праві частини одерж. нерівності
ln (n+1)<( 1+ 1/2 + 1/3+…+1/n) -> Sn , де Sn – частинна сума ряду ∑1/n
Перейшовши у нерівності ln (n+1)< Sn до границі при n-> За теоремою про граничний перехід у нерівності для послідовності одержимо lim Sn =
n->∞
Це означ. що вихідний ряд розбіжний за означ.
Якщо
ряд
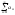 збігається
і має скінченну сумуS
, то ряд
збігається
і має скінченну сумуS
, то ряд
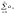 с
також збігається і має суму СS
с
також збігається і має суму СS
Дов-ня:
Нехай
Sn=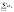 ,n=
,n=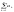 С=сSn.
частинні суми відповідних рядів. Тоді
за озн. суми ряду
С=сSn.
частинні суми відповідних рядів. Тоді
за озн. суми ряду
limn
σn=
limn
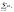 C
= Climn
C
= Climn
 =limn
Sn
=сS.
=limn
Sn
=сS.
2)Якщо
ряди
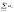 і
і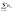 збіг-ся і мають суми А і В то збіжн-ми є
ряди
збіг-ся і мають суми А і В то збіжн-ми є
ряди =А
=А В.
В.
Дов-ня:
Нехай
Sn=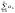 ,
n=
,
n=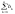
S*n= ,
S*n=
Sn
,
S*n=
Sn n
n
Тоді limn Sn=А , limn n=В.
3)На збіжність не впливає приєднання до нього або відкидання скінченної кількості членів
Нехай
 числовий
ряд з якого відкинемоm
членів суму яких позначимо m
Візьмемо n
настільки великим щоб всі відкинуті
доданки містились у частинній сумі Sn.
Через Сn-m
позначемо
ті доданки, що містяться в Sn
і
не містяться в m
тоді
числовий
ряд з якого відкинемоm
членів суму яких позначимо m
Візьмемо n
настільки великим щоб всі відкинуті
доданки містились у частинній сумі Sn.
Через Сn-m
позначемо
ті доданки, що містяться в Sn
і
не містяться в m
тоді
Sn= сm+n-m тоді limn Sn= сm+ limn n-n.
Звідси випливає що границі у лівій і правій частині одночасно існують або не існують тобто ряд один збіжний(розб-й) коли збіжн-й(розб-й) ряд без m його членів.
Озн:
Вираз
rn
=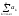 наз.
залишком ряду (1).
наз.
залишком ряду (1).
Із властивості (3) випливає, що ряд 1 збіжний(розбіжний) тоді і тільки тоді, коли збіжним(розбіжним) буде його залишок.
4) якщо ряд 1 збіжний, то limn rn = 0
Доведення:
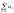 =S
<
=S
<
за озн. Sn + rn = Srn = S- Sn
тоді limn rn = limn (S- Sn)= S- S=0
5)Необхідна умова збіжності .
Якщо ряд 1 збіг-ся то limn аn=0.
Дов-ня:
Нехай
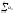 =S<
тоді an
=
Sn
- Sn-1=
=S<
тоді an
=
Sn
- Sn-1=
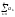 -
-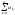 -1=>
limn
an=
limn(
Sn
- Sn-1)=S-
S=0
-1=>
limn
an=
limn(
Sn
- Sn-1)=S-
S=0
Зауваж. Наведена умова є лише необхідною але не достатньою тобто існують розбіжні де limn аn =0
Прикладом такого ряду є ∑1/n
n=1
Достатня умова розбіжності ряду:
Якщо
limn
аn0
то
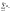 є
розбіжним
є
розбіжним
