
- •2. Неперервність ф-ї багатьох змінних.
- •3. Частинні похідні. Диференціал функцій багатьох змінних.
- •4. Повний диференціал функції багатьох змінних. Диференціали вищих порядків.
- •5. Похідні складної ф-ї багатьох змінних. Диференціал складної ф-ї багатьох змінних.
- •6. Екстремум ф-ї 2 змінних. Необхідні і достатні умови.
- •7. Невласні інтеграли 1 роду. Приклади.
- •8. Невласні інтеграли 2-го роду.
- •9.Числові ряди. Найпростіші властивості.
- •10.Достатні ознаки збіжності додатних числових рядів. Приклади. А).Ознаки порівняння додатніх числових рядів.Приклади.
- •11. Знакопочередні ряди. Ознака Лейбніца. Знакозмінні ряди. Абсолютна і умовна збіжності.
- •12.Функціональні ряди. Поняття рівномірної збіжності. Ознака Вейєрштраса
- •13. Степеневі ряди
- •14. Ряд Тейлора
- •15. Тригонометрический ряд Фур’є
- •16. Подвійний інтеграл умови його існування і властивості.
6. Екстремум ф-ї 2 змінних. Необхідні і достатні умови.
Означення: Нехай z=f(x,y) визначена в області D, а т. М0(х0, у0)єD. Якщо існує такий окіл т. М0 який цілком належить області D для всіх точок М якого відмінних від М0 виконується нерівність f(М) f(М0), то точка М0 називається локальним мінімумом ф-ї z. Якщо за наведених умов для всіх точок М якого відмінних від М0 виконується нерівність f(М)f(М0), то точка М0 називається локальним максимумом ф-ї z. Точки локального максимуму і мінімуму називаються точками екстремуму ф-ї.
Теорема 1(необхідні умови локального екстремуму): Якщо ф-я z=f(x,y) має в т. М0(х0, у0) локальний екстремум, то в цій точці частинні похідні 1 порядку або =0 або не існують.
Доведення:
Нехай т. М0
– локальний екстремум ф-ї f(x,y).
Зафіксуємо y0
. Розглянемо
ф-ю f(x,y0).
Це ф-я однієї змінної. Тоді за відповідною
теоремою, оскільки в x0
для
цієї ф-ї буде екстремум, то
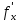 (x0,y0)=0
або не існує. Аналогічно розглядаючи
ф-ю одержимо, що fу’(x0,y0)=0
або не існує.
(x0,y0)=0
або не існує. Аналогічно розглядаючи
ф-ю одержимо, що fу’(x0,y0)=0
або не існує.
Зауваження: Подібна теорема справедлива і для ф-ї n змінних.
Означення: точка М0(х0, у0) в якій fх’М0 = fу’М0 = 0 – стаціонарна точка. Стаціонарні точки, а також точки в яких частинні похідні не існують – критичні точки. Таким чином, (із теор.1) якщо ф-я у якій-небудь точці має локальний екстремум, то ця точка є критичною. Як і для ф-ї однієї змінної обернене твердження не виконується.
Теорема
2 (перші достатні умови локального
екстремуму):
Нехай в стаціонарній точці М0(х0,
у0)
і деякому її околі ф-я f(x,y)
має неперервні частинні похідні 2
порядку. Позначимо через А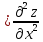 (x0,
y0),
B
(x0,
y0),
B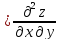 (x0,
y0),
C
(x0,
y0),
C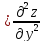 (x0,
y0),
(x0,
y0),
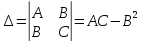 .
Якщо
0,
то
f(x,y)
має в точці М0
локальний
екстремум, причому, якщо А
0, то т. М0
– точка локального мінімуму f(х,у),
а якщо А0,
то т. М0
– точка локального максимуму f(х,у).
У випадку коли 0
f(х,у)
не має в точці М0
локального
екстремуму.
.
Якщо
0,
то
f(x,y)
має в точці М0
локальний
екстремум, причому, якщо А
0, то т. М0
– точка локального мінімуму f(х,у),
а якщо А0,
то т. М0
– точка локального максимуму f(х,у).
У випадку коли 0
f(х,у)
не має в точці М0
локального
екстремуму.
Теорема 3 (2 достатні умови існування екстремуму): Якщо М0(х0, у0) – стаціонарна точка ф-ї z=f(х,у) і d2f(M0), то точка М0 точка локального мінімуму, якщо < 0, то локального максимуму.
7. Невласні інтеграли 1 роду. Приклади.
Нехай
f(x)
визначена на [a;+),
і інтегрована на будь-якому відрізку
[a,b],
де 0аb,
якщо існує скінчена границя
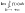 ,
то цю границю називають невласним
інтегралом 1 роду і позначають
,
то цю границю називають невласним
інтегралом 1 роду і позначають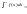
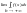 (1).
(1).
Якщо границя в (1) існує і скінченна, то невласний інтеграл наз. збіжним, а ф-я f(x) інтегровна на [а;+ ].
Якщо вказана границя не існує або = , то невласний інтеграл (1) розбіжний, а ф-я f(x) неінтегровна на [а;+ ].Інтеграл (1) не є границею інтегральних сум як визначений інтеграл, а визнач. границя інтегралу із змінною верхнею межею інтегрування.
Геометрично невласний інтеграл визначає площу необмеженної обл.
Аналогічно в ф-лі (1) можна розглянути невласний інтеграл на проміжку [-, b].
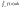 =
=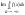 (2) Інтеграл, в якому нескінченні обидві
межі інтегрування визначається так
(2) Інтеграл, в якому нескінченні обидві
межі інтегрування визначається так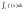 =
=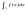 +
+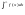 ,
(3)
с-довільне
число. В цьому випадку інтеграл вважається
збіжним, якщо збігаються обидва невласних
інтегралів у правій частині ф-ли (3).
Можна довести, що інтеграл не залежить
від вибору точки с, яка є довільною
точкою на дійсній осі.
,
(3)
с-довільне
число. В цьому випадку інтеграл вважається
збіжним, якщо збігаються обидва невласних
інтегралів у правій частині ф-ли (3).
Можна довести, що інтеграл не залежить
від вибору точки с, яка є довільною
точкою на дійсній осі.
Теорема 1(ознака порівняння)
Нехай
на [a,+)
ф-ї f(x)
і g(x)
неперервні і додатні , і для хє[a,+)
виконується нерівність 0f(x)g(x).
Тоді із збіжності інтегралу
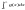 випливає
збіжність
випливає
збіжність а із розбіжності
а із розбіжності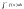 випливає розбіжність
випливає розбіжність Наведена теорема має наступний геом.
зміст:
Наведена теорема має наступний геом.
зміст:
Якщо площа області, що обмежена графіком ф-ції g(x) – скінчене число то площа меншої області, що обмежена зверху графіком f(x) також скінченне число.
Якщо площа меншої області нескінченно велика величина то площа більшої за розміром є також нескінченно велика величина.
Теорема 2(гранична ознака порівняння):
Нехай
ф-ї f(x)
і g(x)
неперервні і додатні на інтервалі
[a,+)
Якщо
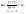 де (0К),
f(x)0
і g(x)0
то інтеграли
де (0К),
f(x)0
і g(x)0
то інтеграли
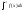 і
і або одночасно збігаються або одночасно
розбігаються.
або одночасно збігаються або одночасно
розбігаються.
У теормах 1 і 2 розглядаються лише невласні інтеграли від невід’ємних ф-й. У випадку коли підінтегральна ф-я знакозмінна справедлива така теорема:
Теорема
3:
Нехай ф-ція f(x)
неперервна на проміжку [a;+).
Якщо збігається
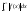 ,
то збігається
,
то збігається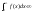 .
.
Твердження
обернене до твердження теореми 3 є
неправильним. Із збіжності
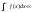 взагалі не випливає збіжність
взагалі не випливає збіжність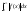
В зв’язку з цим існують спеціальні означення для цих випадків:
-
якщо разом з інтегралом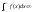 збігається
збігається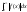 ,
то
,
то наз. абсолютно збіжним.
наз. абсолютно збіжним.
-
якщо
 збіжний
а інтеграл
збіжний
а інтеграл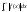 то
то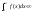 наз. збіжним умовно.
наз. збіжним умовно.
