
- •16. Подвійний інтеграл умови його існування і властивості
- •17. Обчислення подвійних інтегралів. Приклади.
- •18. Заміна змінних в подвійному інтегралі.Подвійний інтеграл у полярних координатах.
- •21. Поняття потрійного інтегралу. Умови його існування та властивості.
- •22. Обчислення потрійного інтегралу. Приклади.
- •23. Заміна зміних у потрійному інтегралі.
- •19. Криволінійні інтеграли. Приклади.
- •20.Ф-ла Гріна
23. Заміна зміних у потрійному інтегралі.
Нехай
в замкненій обмеженій області G
що належить R3
U=f(X,Y,Z)
і Y
![]() за формулами
[X=X(U,V,W)
Y=Y(U,V,W)
Z=Z(U,V,W)](1)
за формулами
[X=X(U,V,W)
Y=Y(U,V,W)
Z=Z(U,V,W)](1)
Треба перейти до нових змінних інтегрування U,V,W.
Будемо
вважати , що область G
при переході до нових змінних перетворюється
на замкнену обмежену область G*
причому
функції (1) мають неперервні частинні
похідні в області G*
і
відмінній від 0 фyнк-ний
визначник:
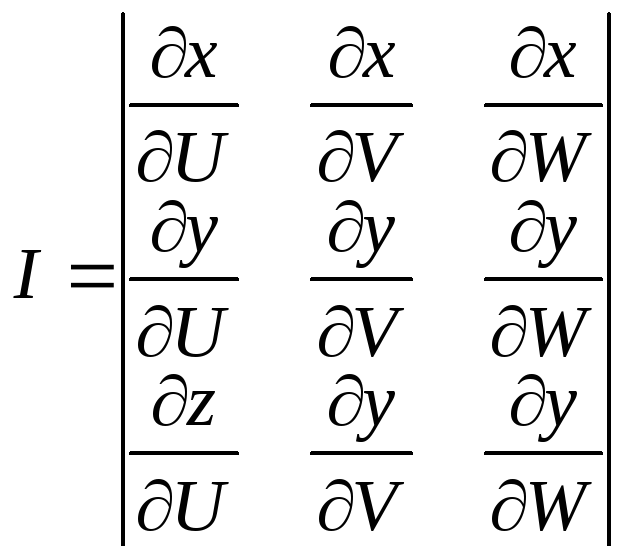
Будемо
вважати крім
того, що функція f(x,y,z)
– неперервна
по області G
тоді справедлива формула
![]()
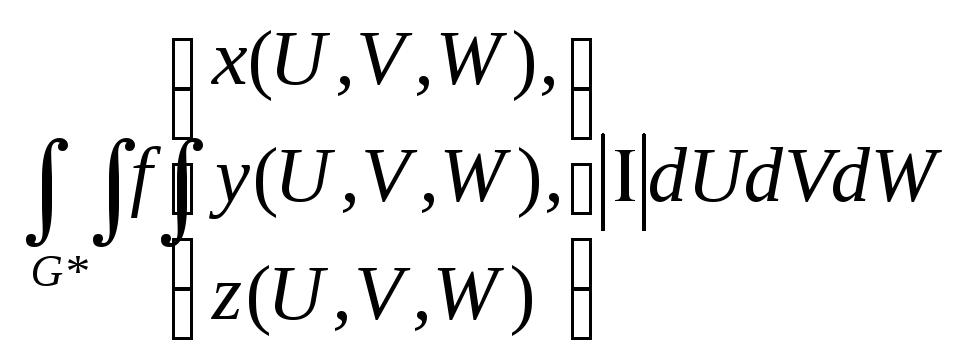 (2)
(2)
При розвязанні задаччі найбільш часто зустрічаються циліндричні та сферичні системи координат. Розглянемо який вигляд має ф-ла(2) у таких координатах:
0 2
0 +
- z +
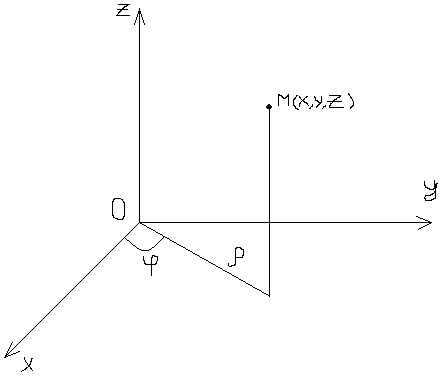
Перехід
від Декартових координат до циліндричних
виконується
за ф-лою
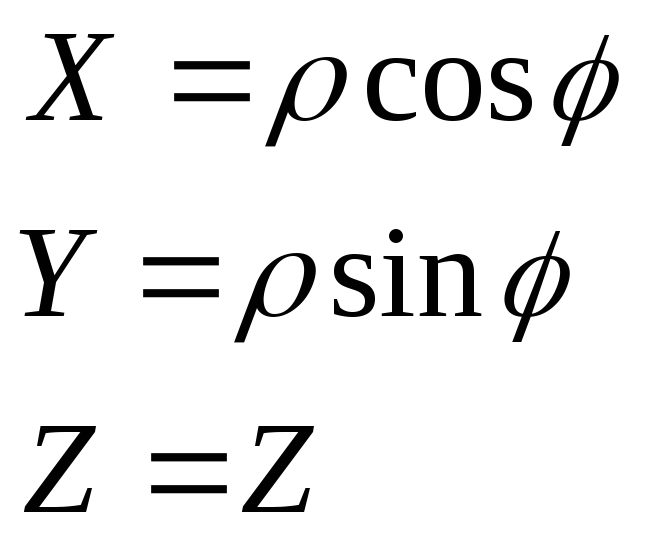
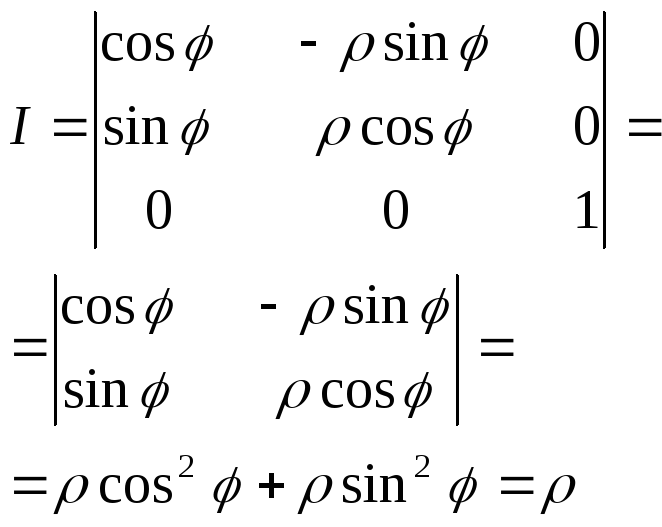
![]()
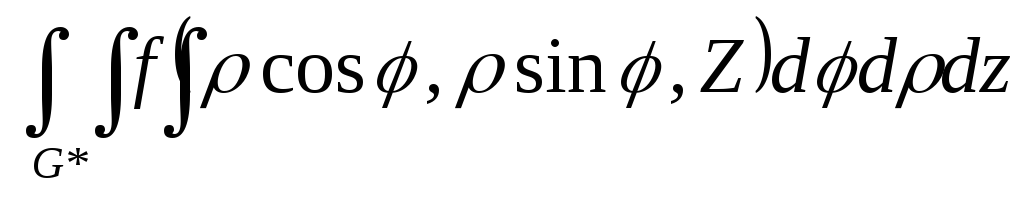 (3)
(3)
Назва циліндричній координати повязана з тим що рівні поверхні =const в цих координатах на точках є циліндр, твірні якого паралельні осі OZ:
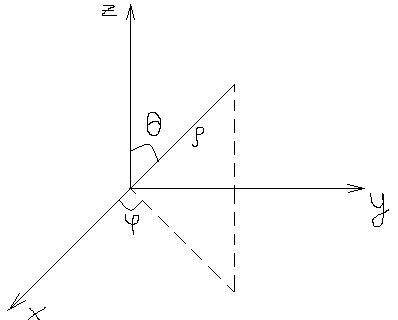
Перехід від Декартовіх координат до сферичних здійснюється за ф-лами :
X=sincos
Y=sin sin
Z=cos
0+
02
0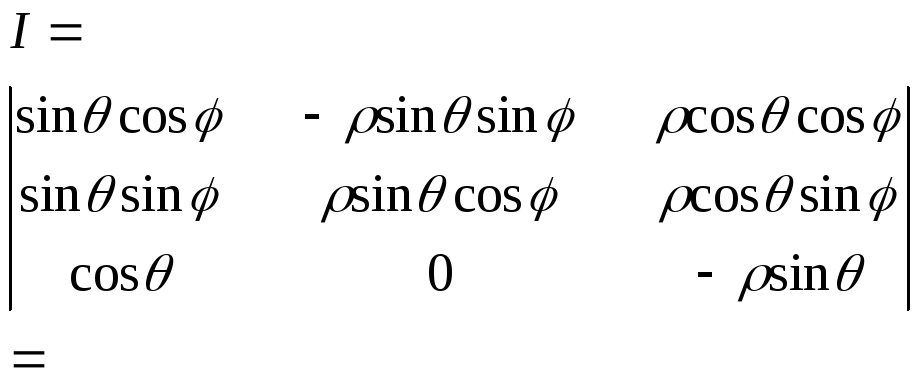
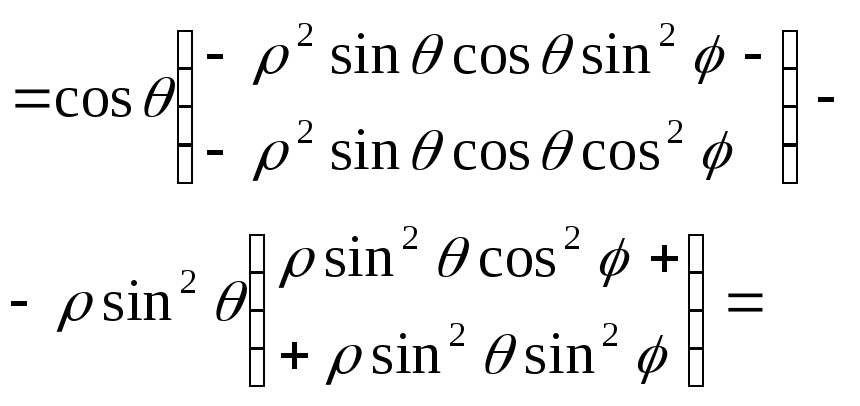
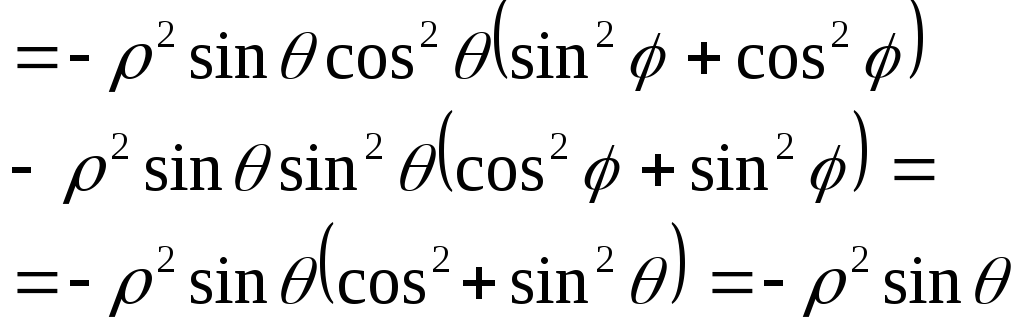
Звідси
![]() і формулу (1) можна записати у вигляді
і формулу (1) можна записати у вигляді
![]()
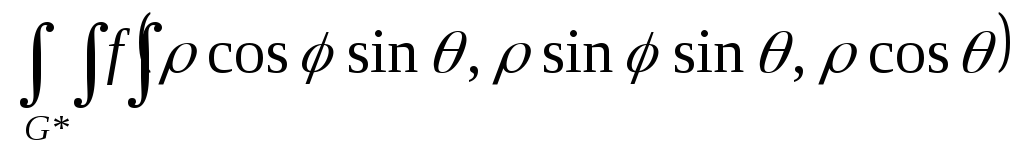 *
*
![]()
(4)
Зауваження: Назва сферичні координати повязані з тим, що координатна поверхння є сферичною.
Зокрема,
якщо обл. G
обмежена циліндричною поверхнею
![]()
та
площинами
![]() , то всі межі інтегрування в циліндричних
координатах будуть сталими, тобто
потрійний інтеграл:
, то всі межі інтегрування в циліндричних
координатах будуть сталими, тобто
потрійний інтеграл:![]()
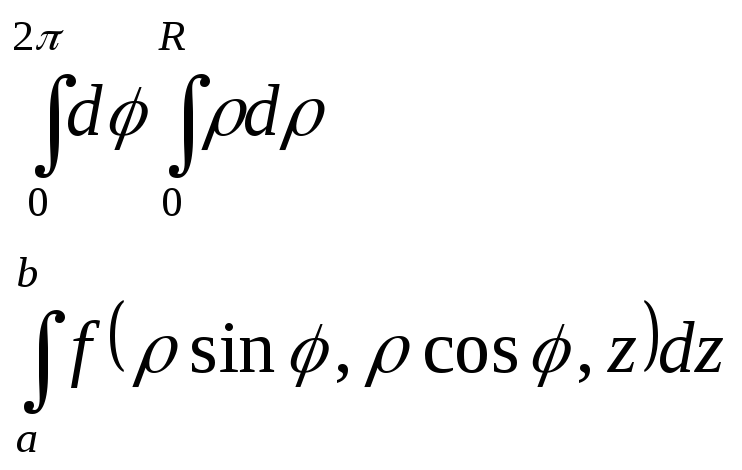
Те
ж саме буде і в сферичних координатах
у випадку , коли обл. G
– куля, або кульове кільце
![]()
x2+y2+z2 = 2sin2cos2 + 2sin2sin2+2cos2=2(sin2(cos2+sin2)+cos2) R R
У
випадку коли G
–
кульове кільце: r2x2+y2+z2R2
![]()
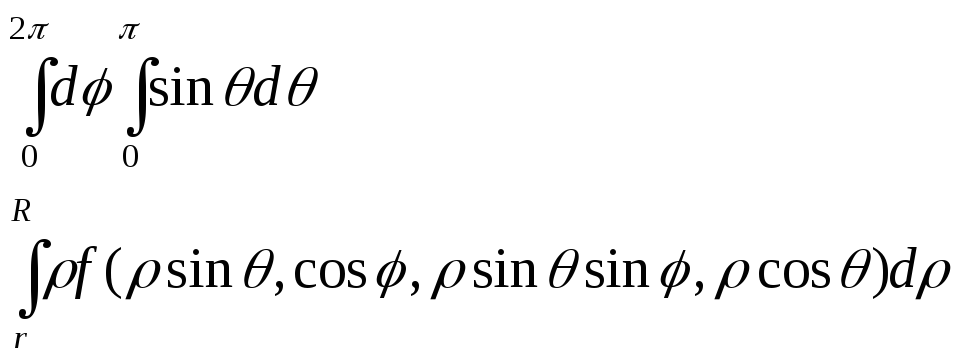 Якщо
G
– куля то в ф-лі [5]
r
треба
взяти r
= 0. Загальних правил, коли треба переходити
до тої або іншої системи координат не
існує, тому часто потрібно записувати
інтеграл у різних системах координат
і лише потім вирішувати в якій із них
обчислювати.
Якщо
G
– куля то в ф-лі [5]
r
треба
взяти r
= 0. Загальних правил, коли треба переходити
до тої або іншої системи координат не
існує, тому часто потрібно записувати
інтеграл у різних системах координат
і лише потім вирішувати в якій із них
обчислювати.
Приклад:
обчислити потр інт
![]()
де
G-куля
![]()
1 За
ф-лами [5],
поклавши
1 За
ф-лами [5],
поклавши
r
= 0 ,
одержимо
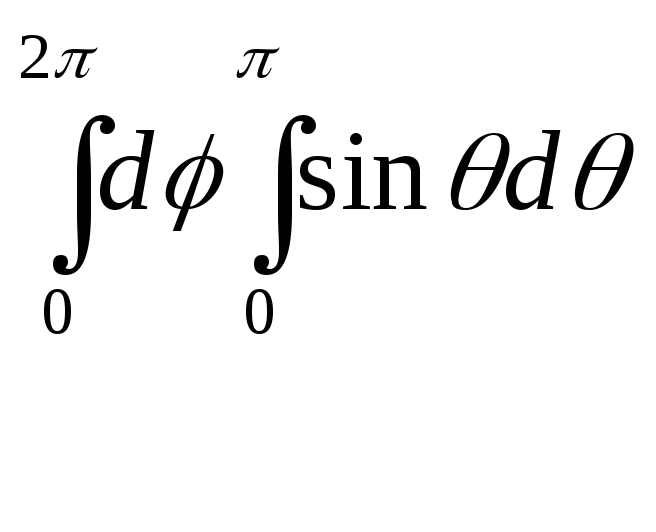
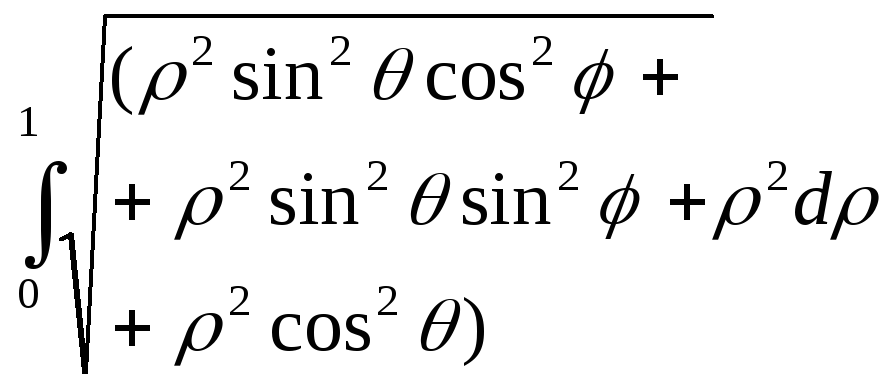
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
19. Криволінійні інтеграли. Приклади.
Озн.:Неперервна крива x=x(t),y=y(t),де а<=t<=b наз. гладкою, якщо ф-ція x(t) і y(t) мають неперервні похідні, які не дорівнюють одночасно 0 ні в якій точці a<=t<=b
Озн:Крива LCR2 наз. Кусково гладкою, якщо вона склад. із скінченого числа гладких кривих.
Нех. в площ. хОу задана кусково гладка крива АВ і нехай на цій кривій визначена обмежена ф-ція F(x,y). Розіб’ємо криву АВ точками А=А0, А1,А2,...,Ап =В на n частин.
На кожній з дуг Аi-1Аi, i=1,n Виберемо довільну точку Мi(ﻉi ,ηi )дуги Ai-1Ai і складемо сумую
![]() (1)
(1)
Озн: сума(1) наз. інтегральною сумою ф-ції f(x,y), по кривій
Позначемо через λ=max з li (найбільша з двох дуг Аi-1 Ai 1≤i≤n), якщо при λ→0 існує скінч. границя інтег. суми (1), яка не залежить від способу розбиття кривої АВ на дуги точками Аi
i=0,n
та не залеж. від точок вибору Мi
,
i=1,n,
то цю границю наз. кринолін. інтег.
першого роду від ф-ції f(x,y).
![]()
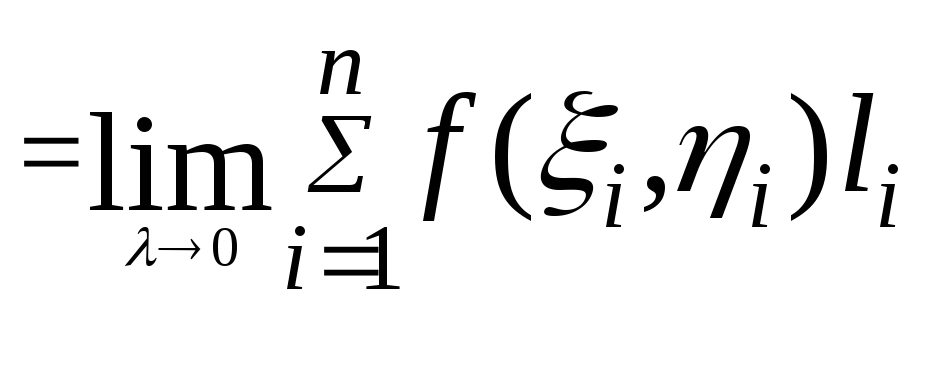 (2)
(2)
якщо границя (2) існує, то ф-цію f(x,y) назю інтегрованою на кривій АВ. Саму криву АВ наз контуром інтегрування. А наз. начальной тч. інтег., В – конечной
Обчислення криволінійних інтегралів I роду:
1)крива АВ задана параметрично x=x(t) y=y(t), a≤t≤b, причому ф-ції x(t), y(t) – неперервні разом із своїми похідними, тоді інт. по АВ
![]()
![]()
АВ задана в явному виді y=y(x), a≤x≤b. Тоді крив. інт.
![]()
![]()
леше вваж., що ф-ція у=у(х) – неперервне разом із своєю похідною y’(x).
3) АВ задане рівн. х=х(у), с≤у≤d. Ми вважаємо, що ф-ція х(у) – неперервна разом зі
своєю похідною x’(y), тоді
![]()
![]() Приклад:
обчислити
Приклад:
обчислити
![]() , АВ: у=х3/4, А(0,0), В(4,3)
, АВ: у=х3/4, А(0,0), В(4,3)
![]()
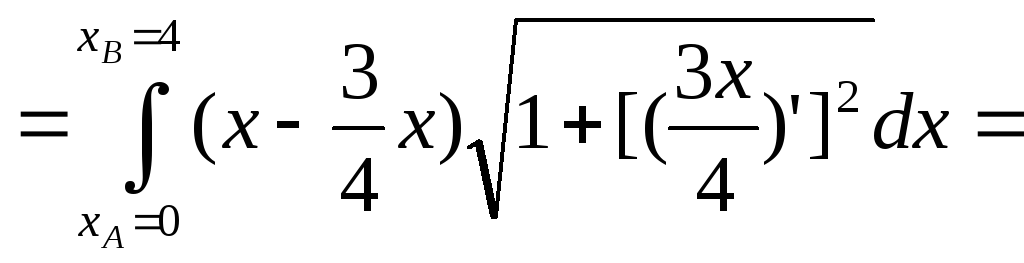
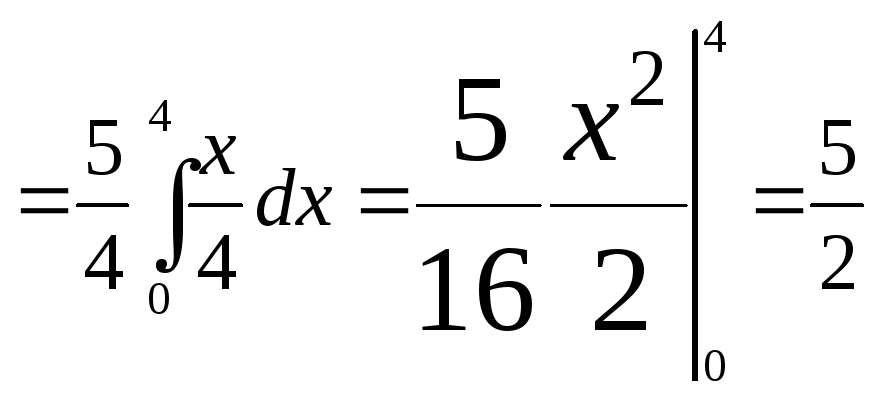 Криволінійні
інтеграли
II
роду визначаються майже так само, як і
криволінійні
інтеграли
I
роду. Нех. в площ. хОу задана кусково
гладка крива А – поч. і В – кін. кривої.
Розіб’ємо на дуги А=А0,А1,...,Аn=В,
на кожній з дуг Аi-1Аi
виберем точку Мi
(ξi,ηi).
Познач. через ⌂хi
проекцію
вектора Аi-1Аi
на
вісь Ox.
Криволінійні
інтеграли
II
роду визначаються майже так само, як і
криволінійні
інтеграли
I
роду. Нех. в площ. хОу задана кусково
гладка крива А – поч. і В – кін. кривої.
Розіб’ємо на дуги А=А0,А1,...,Аn=В,
на кожній з дуг Аi-1Аi
виберем точку Мi
(ξi,ηi).
Познач. через ⌂хi
проекцію
вектора Аi-1Аi
на
вісь Ox.
Нех.
f(x,y)
обмеж. ф-ція, задана на кривій АВ. Розгул.
інт. суму
![]() (3)
(3)
Зрозуміло, що інт. суми в ф-ях (2) і (3) – різні
Озн.
Границя при
![]() інтегральних сум в випадку, коли вона
скінченна не залежить від способу
розбиття кривої АВ не дуги точкам
Аi(=0,n)
і вибору точок Mi(i=1,n)
наз. криволінійним
інтег.
від ф-ції f(x,y)
II
роду по координаті х і позначається
символом
інтегральних сум в випадку, коли вона
скінченна не залежить від способу
розбиття кривої АВ не дуги точкам
Аi(=0,n)
і вибору точок Mi(i=1,n)
наз. криволінійним
інтег.
від ф-ції f(x,y)
II
роду по координаті х і позначається
символом
![]() ,
тобто за означ. Аналогічно визн
,
тобто за означ. Аналогічно визн
![]() .
.![]() кринолін.
інт.
II
роду від ф-ції f(x,y)
по координаті у.
кринолін.
інт.
II
роду від ф-ції f(x,y)
по координаті у.
Нех.
на кривій АВ задані функції P(x,y)
і Q(x,y)
![]() -
наз. криволін. інт.II
роду від ф-цій P
і Q
по кривій АВ і познач символом
-
наз. криволін. інт.II
роду від ф-цій P
і Q
по кривій АВ і познач символом
![]()
Обчислення криволінійних інтегралів II роду:
1)крива АВ задана параметрично x=x(t) y=y(t), a≤t≤b, причому ф-ції x(t), y(t) – неперервні разом із своїми похідними x’(t) і y’(t)
![]()
![]()
![]() 2)АВ
задана в явному виді y=y(x),
a≤x≤b
вваж., що ф-ція у=у(х) – неперервне разом
із своєю похідною y’(x).
Тоді крив. інт. II
роду
2)АВ
задана в явному виді y=y(x),
a≤x≤b
вваж., що ф-ція у=у(х) – неперервне разом
із своєю похідною y’(x).
Тоді крив. інт. II
роду
![]()
![]() 3)АВ
задане рівн. х=х(у), с≤у≤d.
Ми
3)АВ
задане рівн. х=х(у), с≤у≤d.
Ми
вважаємо,
що ф-ція х(у) – неперервна разом зі
своєю похідною x’(y), тоді
![]()
![]() Пример
обчислити
Пример
обчислити
![]() ,
АВ: у=х2
парабола,
яка з’єднує тч. А(0,0) і В(1,1)
,
АВ: у=х2
парабола,
яка з’єднує тч. А(0,0) і В(1,1)
За
другою ф-лою
![]()
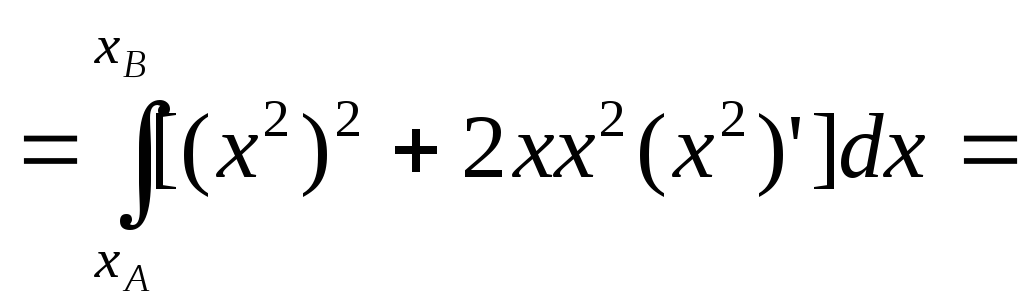
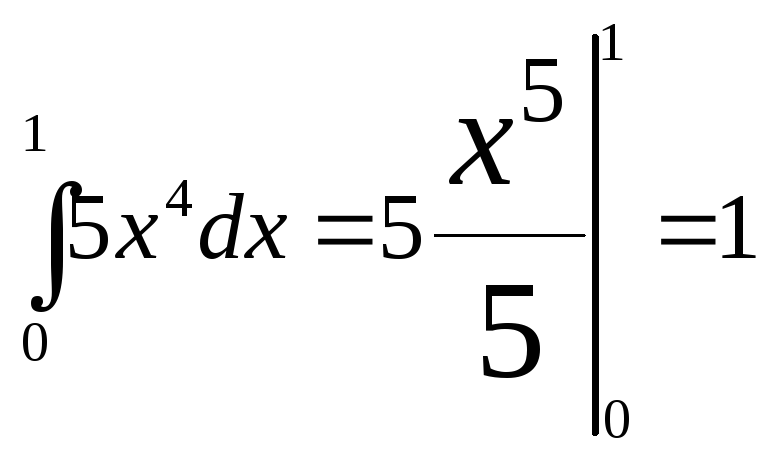
У деяких випадках треба обчислювати крив. інтеграл по замкненому контуру.
В
цьому випадку розглядають дві орієнтації:
під додатною орієнтацією контура
розуміють обхід контура у напрямі, що
збігається з напрямом, який протилежний
руху годинникової стрілки. Тобто це
буде такий обхід обл., при якому
внутрішність обл., яка обмежена кривою
АВ залишається зліва. Крив. інтеграл по
замкненому контуру познач. символом
![]() ;
при обхіді контуру (за годинниковою
стрілкою) вважають від’ємною і познач.
символом
;
при обхіді контуру (за годинниковою
стрілкою) вважають від’ємною і познач.
символом![]()
