§4. Замкнені підмножини топологічного простору

- топологічний простір, називаєтьсязамкненою, якщо - відкрита множина.

Приклад 1:

- метричний простір, як було доведено раніше і- відкриті множини, тому множинитає множинами замкненими

.

Приклад 2:

У дискретній топології замкненими будуть усі підмножини, оскільки в ній всі підмножини відкриті.

Приклад 3:

У топології скінченних доповнень, задані на нескінченній множині Т (топології Заріського) замкненими будуть та усі скінченні підмножини з Т.

Теорема 1 (властивості замкнених підмножин):

Нехай - топологічний простір.-сукупність усіх замкнених підмножин цього простору, тодімає наступні властивості:

1.

2.Перетин будь-якої сукупності замкнених підмножин з Т є підмножина замкнена.

3. Об’єднання будь-якої скінченної сукупності замкнених підмножин з Т є підмножина замкнена.

підмножиною, оскільки її доповнення не є відкритою.

Теорема 2 (про введення топології за допомогою системи замкнених підмножин):

Нехай Т – деяка множина, , що задовольняє вимогам (1)-(3) попередньої теореми, тоді на множині Т існує топологія, для якоїє системою замкнених підмножин.

§5. Внутрішні точки. Внутрішність підмножини топологічного простору

Т – топологічний простір, Довільна відкрита підмножина з Т, що містить А називається(відкритим) околом множини А.

Нехай Т – топологічний простір, Точканазиваєтьсявнутрішньою точкою А, якщо .

Сукупність усіх внутрішніх точок множини А називають внутрішністю цієї множини (Int A)

Твердження 1: Нехай Т – топологічний простір, ТодіInt A співпадає з об’єднанням усіх відкритих підмножин, що містяться в А.

Наслідок 1: IntA є найбільшою відкритою підмножиною, що міститься в А.

Наслідок 2: Множина А є відкритою тоді і тільки тоді, коли А=IntA.

Приклад 1: Розглянемо простір R, тоді Int [a, b]=(a, b)

Приклад 2: РозглянемоR, . Оскільки будь-який відкритий окіл як раціональні, так і ірраціональні числа, то

§6. Точки дотику. Замикання підмножин топологічного простору

Нехай Т – топологічний простір, називаєтьсяточкою дотику до підмножини А, якщо .

Сукупність усіх точок дотику А називається замиканням підмножини А. ([А])

Теорема (властивості операції замикання):

Нехай Т – топологічний простір, тоді операція замикання в Т має такі властивості:

1.

2.

3.

4.

Наслідок. Нехай Т – топологічний простір, - замкнена тоді і тільки тоді, коли

.

Твердження: Нехай Т – топологічний простір, Тоді- перетин усіх замкнених підмножин з Т, що містять А.

§7. Ізольовані, граничні, межові точки

Нехай Т – топологічний простір, Тоді

Точка К, яка належить множині А, називається ізольованою точкою множини А, якщо

Множина усіх ізольованих точок з А позначається IsA.

Точка х, яка належить множині Т, називається граничною, якщо

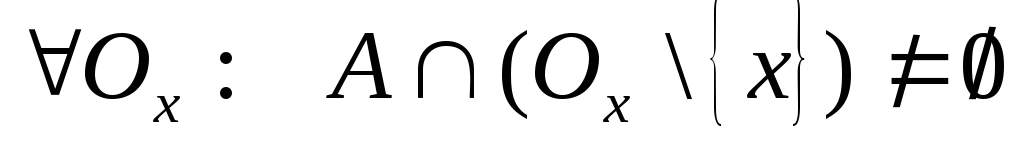. Множина усіх граничних точок А позначається і називається похідною множини А.

Точка х, яка належить множині Т, називається межовою точкою множини А, якщо . Сукупність межових точок – це межа А (FrA).

Твердження 1: Нехай Тодірозпадається на три множини, що не перетинаються:

1. IsA.

2. - граничні точки А, що належать А.

3. - граничні точки А, що не належать А.

Наслідок 1: Підмножина А множини Т є замкненою тоді і тільки тоді, коли вона містить усі свої граничні точки.

Твердження 2: Нехай Тодірозпадається в об’єднання трьох підмножин, що не перетинаються:

1. 

2. 

3. 

Наслідок 2: є замкненою тоді і тільки тоді, коли вона містить усі свої межові точки.

Наслідок 3: Тоді:

1.

2.

3.

Приклади: 1.

2.