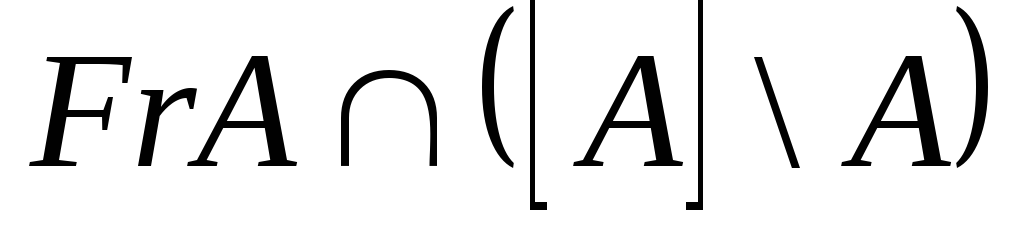§6. Точки дотику. Замикання підмножин топологічного простору

Нехай Т – топологічний простір, називаєтьсяточкою дотику до підмножини А, якщо .

Сукупність усіх точок дотику А називається замиканням підмножини А. ([А])

Теорема (властивості операції замикання):

Нехай Т – топологічний простір, тоді операція замикання в Т має такі властивості:

1.

2.

3.

4.

Доведення: 1)

2)

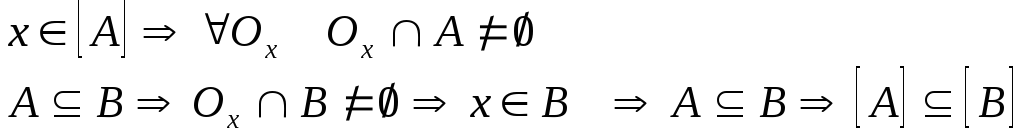
3)

Покажемо, що

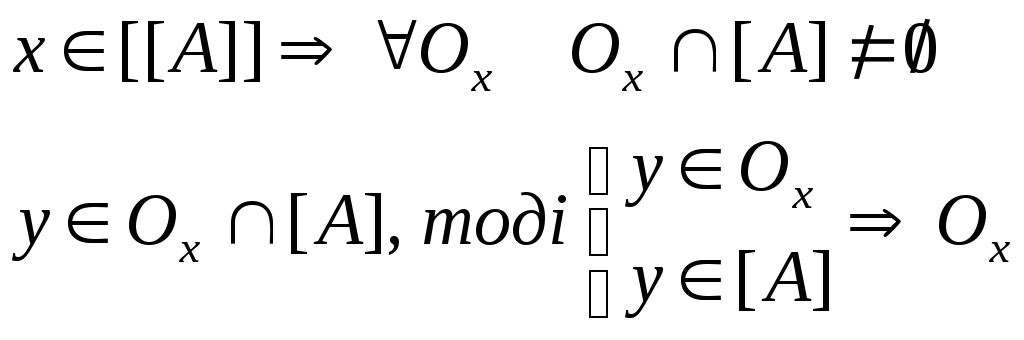
Можна розглядати як окіл у, а оскільки ує[А], то

4)

Покажемо, що

Застосуємо метод математичної індукції:

Базис

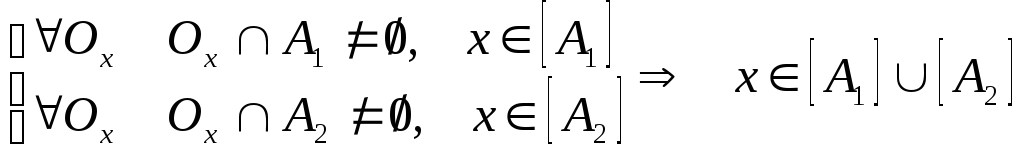
Індуктивне припущення:

Індуктивний перехід: .

Все доведено.

Нехай Т – топологічний простір, - замкнена тоді і тільки тоді, коли

.

Доведення: Припустимо, що А – замкнена, тоді - відкрита, тобто

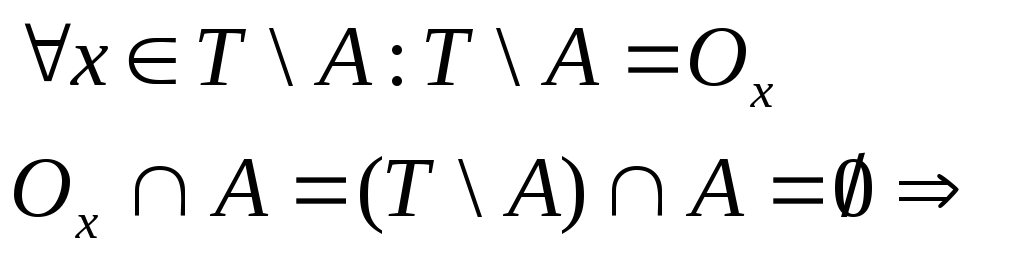
хне є точкою дотику.

Отже, не містить точок дотику, тому вони попадають в А. Але.

Припустимо тепер, що , слідовно всі точки дотику містяться в А, томуне має точок дотику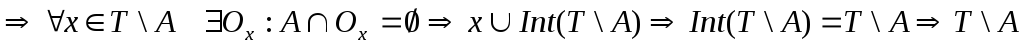- відкрита, тому А – замкнена. Все доведено.

Твердження: Нехай Т – топологічний простір, Тоді- перетин усіх замкнених підмножин з Т, що містять А.

Доведення: Нехай F – перетин усіх замкнених підмножин з Т, що містять А.

Тоді F – замкнена підмножина, яка містить А.

Покажемо, що . Дійсно, оскількивідкрита, то

х не є точкою дотику до А, тому усі точки дотику містяться в F.

Оскільки , то- замкнена.

§7. Ізольовані, граничні, межові точки

Нехай Т – топологічний простір, Тоді

Точка К, яка належить множині А, називається ізольованою точкою множини А, якщо

Множина усіх ізольованих точок з А позначається IsA.

Точка х, яка належить множині Т, називається граничною, якщо

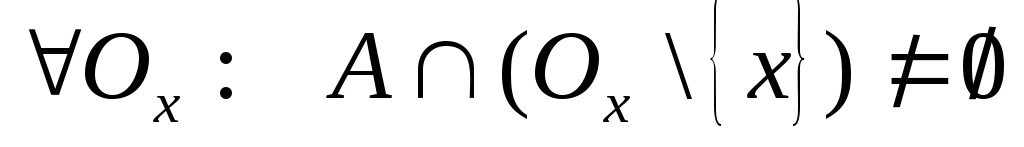. Множина усіх граничних точок А позначається і називається похідною множини А.

Точка х, яка належить множині Т, називається межовою точкою множини А, якщо . Сукупність межових точок – це межа А (FrA).

Твердження 1: Нехай Тодірозпадається на три множини, що не перетинаються:

1. IsA.

2. - граничні точки А, що належать А.

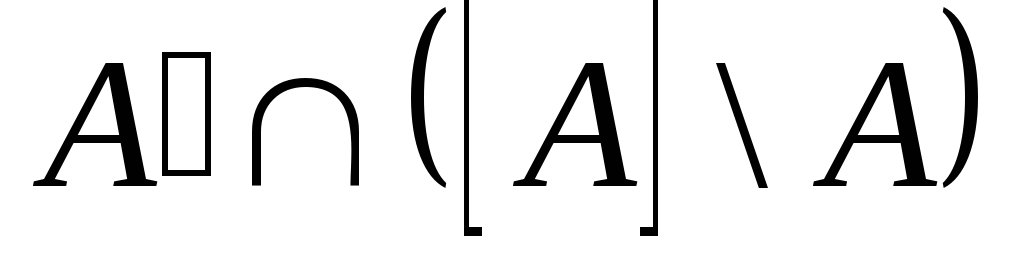3. - граничні точки А, що не належать А.

Доведення: З означення граничної точки та точок дотику випливає, що будь-яка гранична точка є точкою дотику: .

А розглянувши ще означення ізольованих точок , бачимо, що будь-яка точка дотику є або граничною точкою, або ізольованою:

Оскільки означення ізольованих і граничних точок є несумісними, то перетин – пуста множина: .

Множина розпадається в об’єднання двох підмножин, що не перетинаються: . Все доведено.

Наслідок 1: Підмножина А множини Т є замкненою тоді і тільки тоді, коли вона містить усі свої граничні точки.

Твердження 2: Нехай Тодірозпадається в об’єднання трьох підмножин, що не перетинаються:

1. 

2. 

3. 

Доведення: З означення межових точок та точок дотику випливає, що всяка межова точка є точкою дотику, тобто . Розглянувши ще означення внутрішніх точок, бачимо, що будь-яка точка дотику є або межовою, або внутрішньою точкою (якщо ).

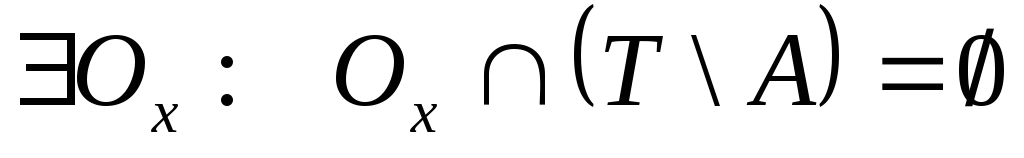Таким чином, .

Оскільки означення межових та внутрішніх точок є несумісними, то .

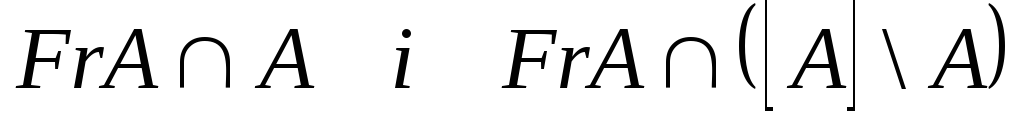У свою чергу, розпадається в об’єднання двох підмножин, що не перетинаються: . Все доведено.

Наслідок 2: є замкненою тоді і тільки тоді, коли вона містить усі свої межові точки.

Наслідок 3: Тоді:

1.

2.

3.

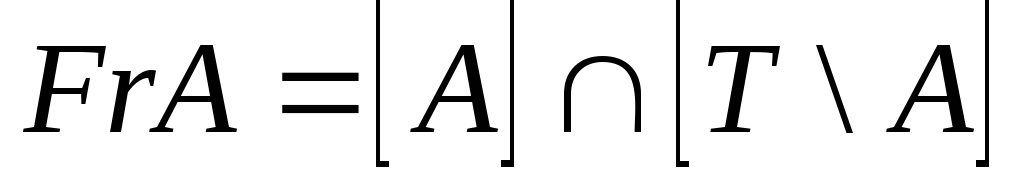
Приклади: 1.

2.