
- •Практикум з курсу
- •Метричні й топологічні простори Варіант 1
- •Варіант 2
- •Варіант 3
- •Варіант 4
- •Варіант 5
- •Варіант 6
- •Варіант 7
- •Варіант 8
- •Варіант 9
- •Скрізь щільні та ніде не щільні множини. Сепарабельні простори. Неперервні відображення Варіант 1
- •Варіант 2
- •Варіант 3
- •Варіант 8
- •Варіант 9
- •4.Аксіоми зчисленності та відокремленості. Нормальні простори. Гомеоморфні простори Варіант 1
- •Варіант 2
- •Варіант 3
- •Варіант 4
- •Варіант 5
- •Варіант 6
- •Варіант 7
- •Варіант 7
- •Варіант 4
- •Список рекомендованої літератури
Варіант 5
Нехай β – база топологічного простору
 і
і .
Довести, що сім’я
.
Довести, що сім’я
 де
де
 утворює базу в підпросторі
утворює базу в підпросторі
 .
.Довести, що в
 – просторі точка, база якої складається
із скінченного числа елементів,
ізольована.
– просторі точка, база якої складається
із скінченного числа елементів,
ізольована.Довести, що в означенні регулярного простору аксіому
 можна замінити на аксіому
можна замінити на аксіому .
Чи виконується це твердження для
нормальних просторів?
.
Чи виконується це твердження для
нормальних просторів?Нехай
 ,
,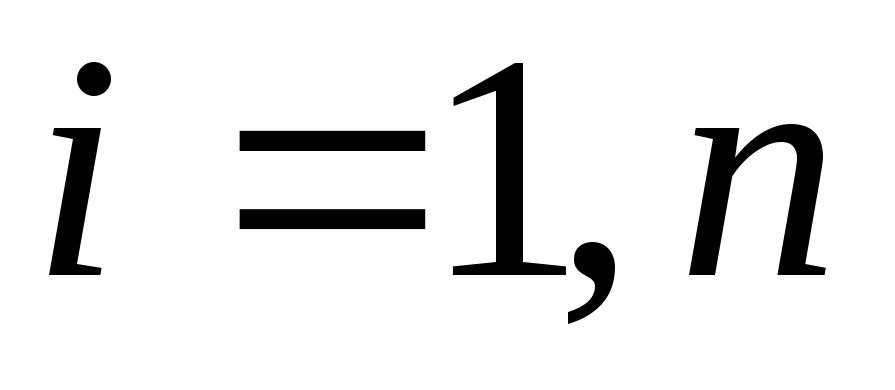 – неперервні відображення топологічного
простору
– неперервні відображення топологічного
простору
 в
в
 .
Довести, що підмножина топологічного
простору
.
Довести, що підмножина топологічного
простору
 ,
яка складається із всіх розв’язків
системи рівнянь
,
яка складається із всіх розв’язків
системи рівнянь

 ,
буде замкненою. Чи можна скінченну
систему рівнянь замінити нескінченною?
,
буде замкненою. Чи можна скінченну
систему рівнянь замінити нескінченною?
Варіант 6
Довести, що топологічний добуток скінченного числа топологічних просторів з другою аксіомою зчисленності буде топологічним простором з другою аксіомою зчисленності. Чи виконується обернене твердження?
Довести, що підмножина топологічного простору з першою аксіомою зчисленності замкнена тоді і тільки тоді, коли межа будь-якої збіжної в
 послідовності з
послідовності з
 належить
належить
 .
.Нехай
 – множина дійсних чисел. Довести, що
сім’я всіх інтервалів типу
– множина дійсних чисел. Довести, що
сім’я всіх інтервалів типу ,
, буде базою деякої топології τ на множині
буде базою деякої топології τ на множині .
Довести, що
.
Довести, що – нормальний простір.
– нормальний простір.Нехай
 ,
, – неперервні відображення топологічного
простору
– неперервні відображення топологічного
простору
 в
в
 .
Довести, що підмножина топологічного
простору
.
Довести, що підмножина топологічного
простору
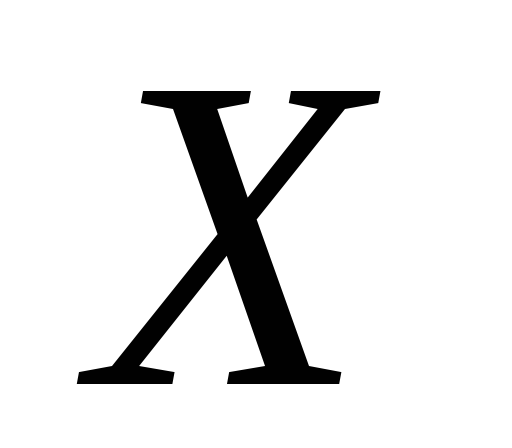 ,
яка складається із всіх розв’язків
системи рівнянь
,
яка складається із всіх розв’язків
системи рівнянь

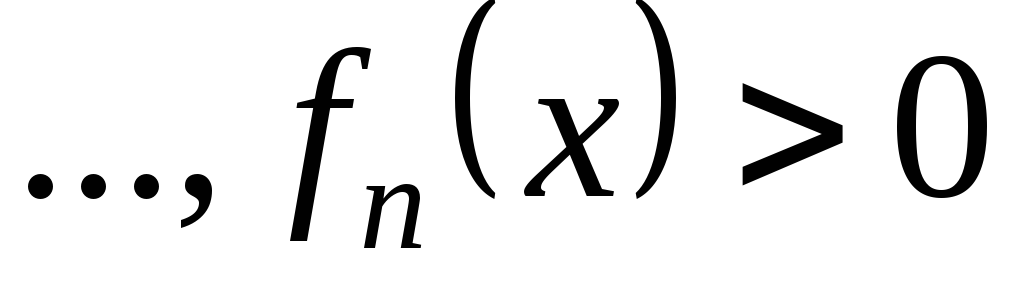 ,
буде відкритою. Чи можна скінченну
систему рівнянь замінити нескінченною?
,
буде відкритою. Чи можна скінченну
систему рівнянь замінити нескінченною?
Варіант 7
Довести, що будь-який підпростір простору з другою аксіомою зчисленності буде простором з другою аксіомою зчисленності.
Довести, що будь-який підпростір
 – простору буде
– простору буде – простором.
– простором.Довести, що
 – простір буде нормальним тоді і тільки
тоді, коли для будь-яких двох замкнених
неперетинних у ньому підмножин існує
такий окіл однієї з них, що його замикання
не перетинається з іншими.
– простір буде нормальним тоді і тільки
тоді, коли для будь-яких двох замкнених
неперетинних у ньому підмножин існує
такий окіл однієї з них, що його замикання
не перетинається з іншими.Довести, що вся площина
 2
гомеоморфна до будь-якого відкритого
квадрату цієї площини.
2
гомеоморфна до будь-якого відкритого
квадрату цієї площини.
Варіант 8
Навести приклад, який довів би, що неперервний образ простору з другою аксіомою зчисленності може не задовольняти цій аксіомі.
Довести, що у
 – просторі будь-яка множина буде
перетином деякої сім’ї
відкритих множин.
– просторі будь-яка множина буде
перетином деякої сім’ї
відкритих множин.Довести, що
 – простір
– простір
 тоді і тільки тоді регулярний, коли для
будь-якої точки
тоді і тільки тоді регулярний, коли для
будь-якої точки
 та будь-якої замкненої множини
та будь-якої замкненої множини
 ,
що не містить цю точку, існує такий окіл
,
що не містить цю точку, існує такий окіл ,
для якого
,
для якого
 .
.Довести, що будь-який відкритий прямокутник в
 2
буде
гомеоморфний в
2
буде
гомеоморфний в
 2.
2.
Варіант 9
Довести, що образ бази при неперервних відображеннях може не бути базою.
Навести приклад
 – простору, у якому ніяка множина з
однією точкою не є замкненою.
– простору, у якому ніяка множина з
однією точкою не є замкненою.Довести, що образ нормального простору при неперервному замкненому відображенні буде нормальним простором.
Довести, що замкнений круг в
 2
буде
гомеоморфний до замкненого квадрату
в
2
буде
гомеоморфний до замкненого квадрату
в
 2.
2.
Зв’язність топологічних просторів.
Лінійна зв’язність. Гомеоморфізм
Варіант 1
Навести приклад двох зв’язних множин, перетин яких не буде зв’язною множиною.
Навести приклад, який підтверджує, що прообраз зв’язної множини при неперервному відображенні не обов’язково буде зв’язним.
Нехай
 – графік функції
– графік функції
 .
Довести, що множина
.
Довести, що множина
 2
– зв’язна, але не лінійно зв’язна.
2
– зв’язна, але не лінійно зв’язна.Визначити, чи будуть гомеоморфні «букви»
 і
і
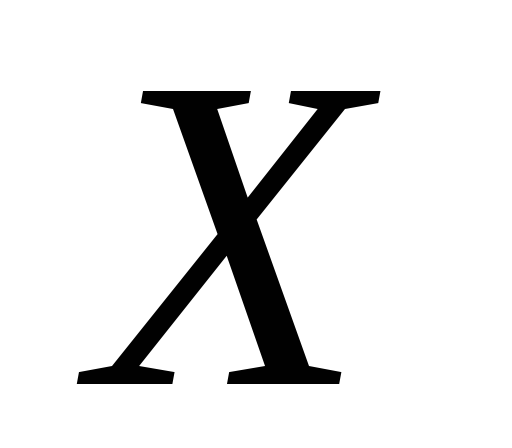 на площині.
на площині.
Варіант 2
Визначити, чи буде зв’язною множина точок площини, що містить тільки одну раціональну координату.
Визначити, чи буде локально зв’язною підмножина точок


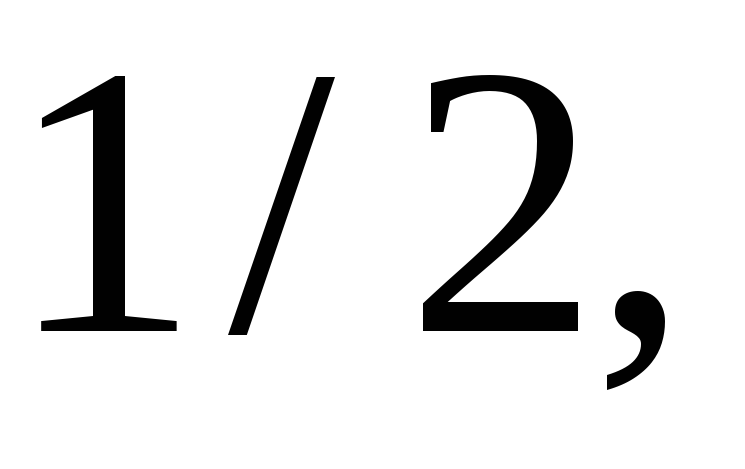

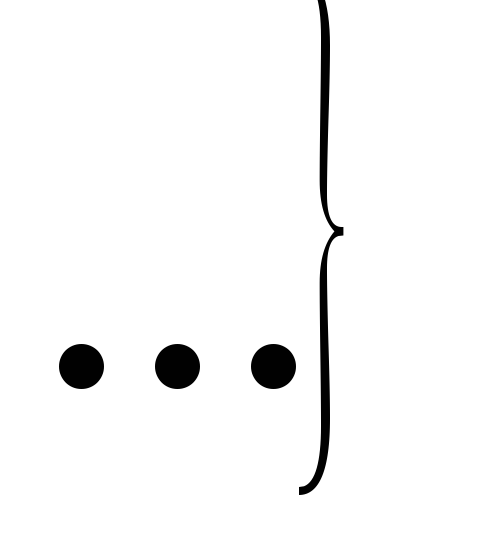 числової прямої.
числової прямої.Нехай
 і
і –
топологічні простори. Довести, що
–
топологічні простори. Довести, що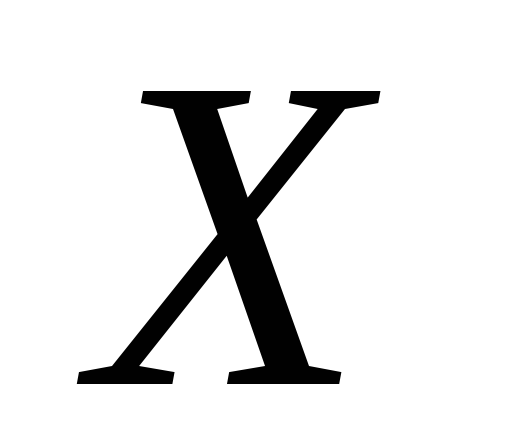 і
і тоді і тільки тоді зв’язні, коли
топологічний простір
тоді і тільки тоді зв’язні, коли
топологічний простір – зв’язний.
– зв’язний.Визначити, чи будуть гомеоморфні «букви»
 і
і
 на площині.
на площині.
Варіант 3
Визначити, чи буде зв’язною множина точок площини, що мають хоча б одну раціональну координату.
Нехай

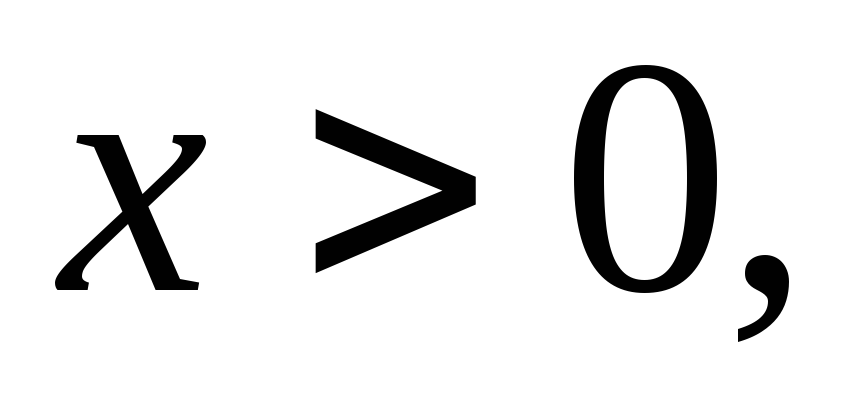
 та
та .
Довести, що
.
Довести, що – лінійно зв’язна множина, а
– лінійно зв’язна множина, а
 –
зв’язна, але не лінійно зв’язна
–
зв’язна, але не лінійно зв’язнаДовести, що зв’язність топологічного простору
 є
те саме, що: будь-яка неперервна функція
є
те саме, що: будь-яка неперервна функція задовольняє
властивостям Дарбу, тобто разом з
будь-якими двома своїми значеннями
приймає і всі проміжні значення.
задовольняє
властивостям Дарбу, тобто разом з
будь-якими двома своїми значеннями
приймає і всі проміжні значення.Визначити, чи будуть гомеоморфними
 2
2 і
і
 2
2 .
.
Варіант 4
Визначити, чи буде зв’язною множина точок площини, що має точно дві раціональні координати.
Визначити, чи буде локально зв’язною множина всіх цілих чисел у топології, яка індукована з
 1.
1.Довести, що якщо множина
 –
зв’язна, то будь-яка множина
–
зв’язна, то будь-яка множина
 така,
що
така,
що
 ,
також буде зв’язною.
,
також буде зв’язною.Визначити, чи будуть гомеоморфними кулі в
 2
та коло в
2
та коло в
 2.
2.
Варіант 5
Довести, що топологічний простір
 незв’язний тоді і тільки тоді, коли
існує власна підмножина
незв’язний тоді і тільки тоді, коли
існує власна підмножина

 цього простору така, що
цього простору така, що

 .
.Навести опис усіх зв’язних підмножин множини дійсних чисел, що наділені топологією скінченних доповнень.
Нехай
 – шлях, що з’єднує точку множини
– шлях, що з’єднує точку множини
 з точкою, що належить
з точкою, що належить .
Довести, що
.
Довести, що

 ,
тобто шлях перетинає межу множини
,
тобто шлях перетинає межу множини
 .
.Довести, що відкритий інтервал не гомеоморфний ніякому напіввідкритому і ніякому замкненому інтервалу.
Варіант 6
Довести, що простір
 незв’язний тоді і тільки тоді, коли
його можна неперервно сюр’єктивно
відобразити в гаусдорфів простір, який
складається з двох точок.
незв’язний тоді і тільки тоді, коли
його можна неперервно сюр’єктивно
відобразити в гаусдорфів простір, який
складається з двох точок.Визначити, чи буде локально зв’язною множина всіх раціональних чисел з топологією, яка індукована з
 1.
1.Нехай
 – підмножина лінійно зв’язного
топологічного простору. Довести, що
якщо
– підмножина лінійно зв’язного
топологічного простору. Довести, що
якщо
 –
лінійно зв’язна, то і
–
лінійно зв’язна, то і
 також лінійно зв’язна множина.
також лінійно зв’язна множина.Визначити, чи будуть гомеоморфними коло в
 2
та кругове кільце в
2
та кругове кільце в
 2.
2.
