
- •Практикум з курсу
- •Метричні й топологічні простори Варіант 1
- •Варіант 2
- •Варіант 3
- •Варіант 4
- •Варіант 5
- •Варіант 6
- •Варіант 7
- •Варіант 8
- •Варіант 9
- •Скрізь щільні та ніде не щільні множини. Сепарабельні простори. Неперервні відображення Варіант 1
- •Варіант 2
- •Варіант 3
- •Варіант 8
- •Варіант 9
- •4.Аксіоми зчисленності та відокремленості. Нормальні простори. Гомеоморфні простори Варіант 1
- •Варіант 2
- •Варіант 3
- •Варіант 4
- •Варіант 5
- •Варіант 6
- •Варіант 7
- •Варіант 7
- •Варіант 4
- •Список рекомендованої літератури
Варіант 8
Довести, що підмножина
 топологічного простору
топологічного простору
 ніде не щільна в
ніде не щільна в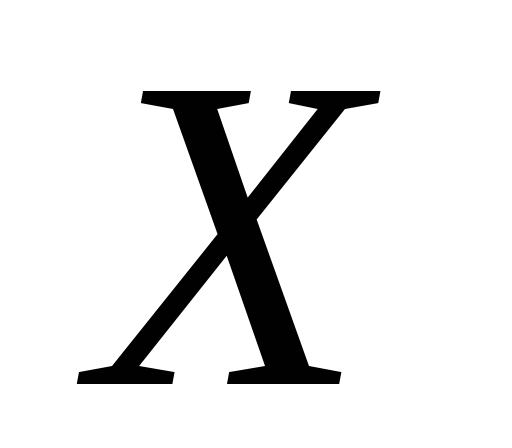 тоді і тільки тоді, коли в будь-якій не
порожній відкритій множині
тоді і тільки тоді, коли в будь-якій не
порожній відкритій множині існує така не порожня відкрита множина
існує така не порожня відкрита множина ,
що
,
що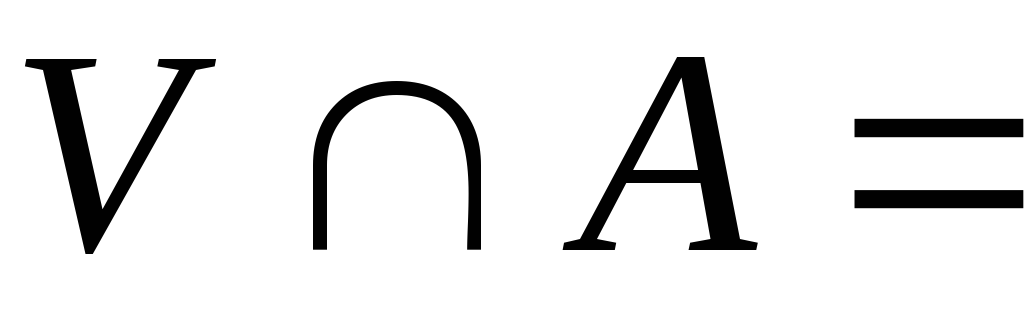
 .
.Нехай
 – ніде не щільна в топологічному
просторі
– ніде не щільна в топологічному
просторі
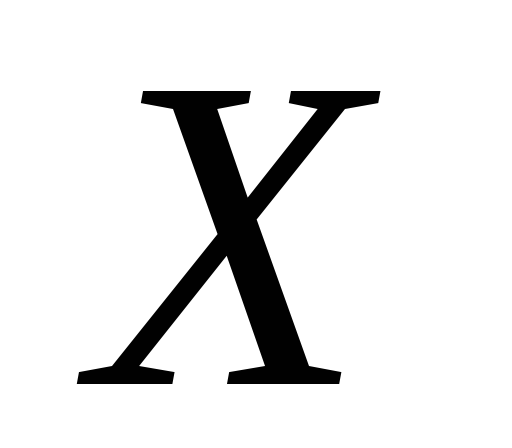 та
та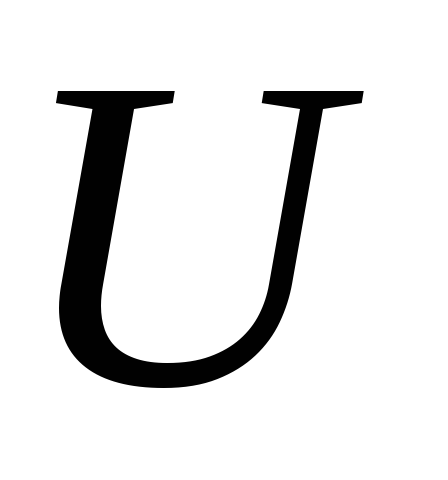 –
довільна відкрита в
–
довільна відкрита в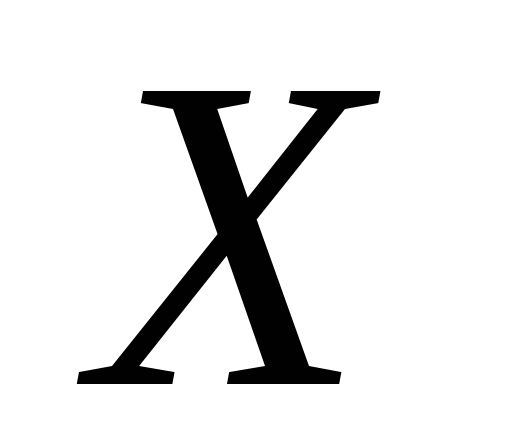 множина. Довести, що множина
множина. Довести, що множина
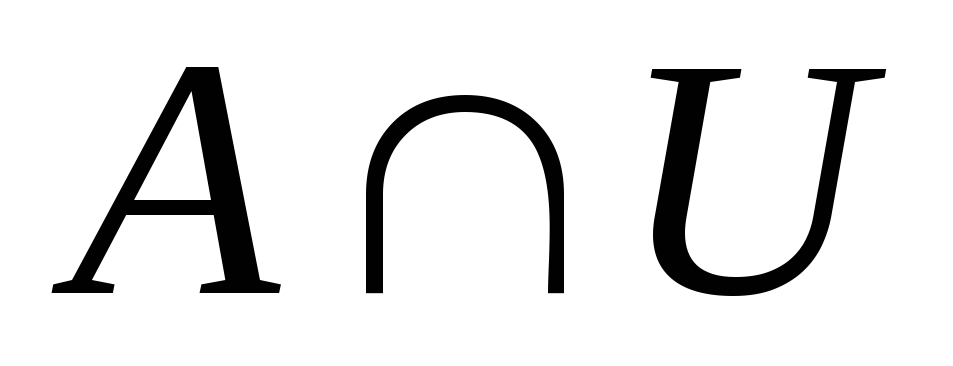 ніде не щільна в
ніде не щільна в
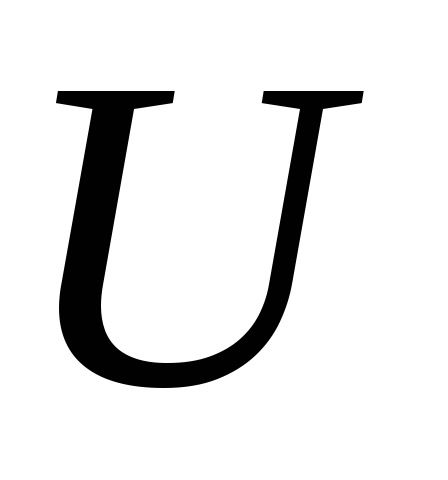 (
( розглядається
як підпростір
розглядається
як підпростір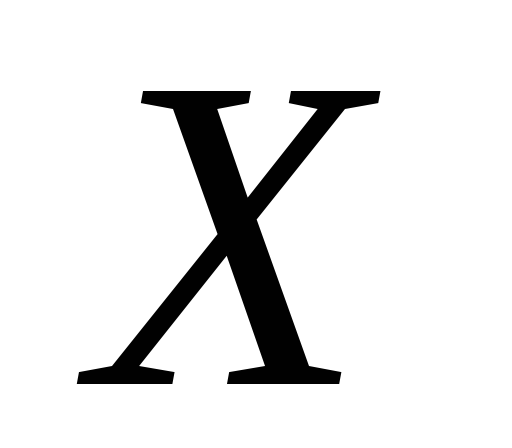 ).
).Довести, що якщо в топологічному просторі
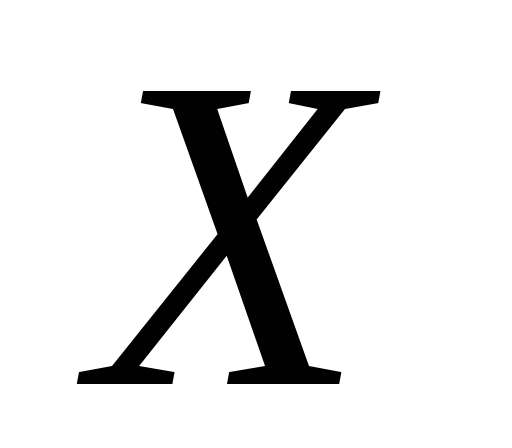 є
така зчисленна сім’я
не порожніх відкритих множин, що будь-яка
не порожня відкрита множина
є
така зчисленна сім’я
не порожніх відкритих множин, що будь-яка
не порожня відкрита множина
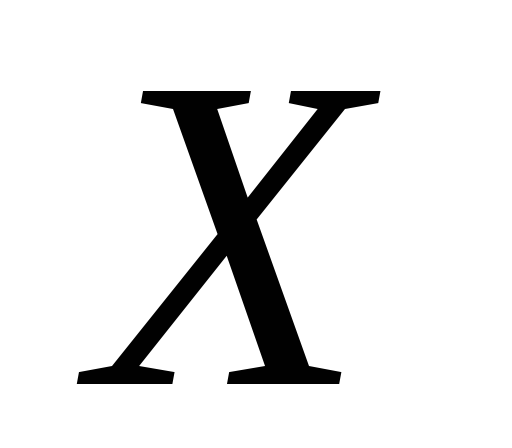 містить елемент (хоч один) цієї сім’ї,
то будь-який скрізь щільний в
містить елемент (хоч один) цієї сім’ї,
то будь-який скрізь щільний в
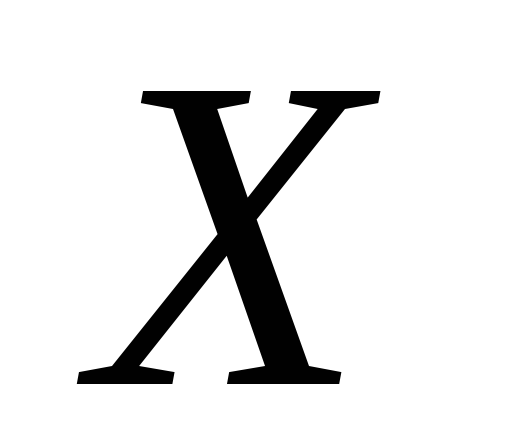 підпростір буде сепарабельним.
підпростір буде сепарабельним.Довести, що відображення
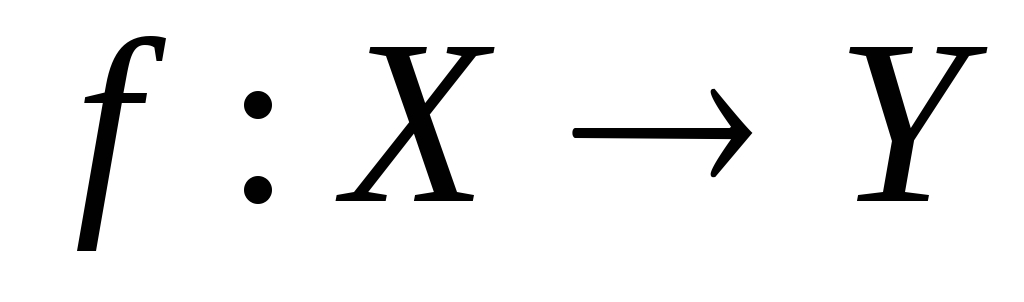 топологічних просторів
топологічних просторів
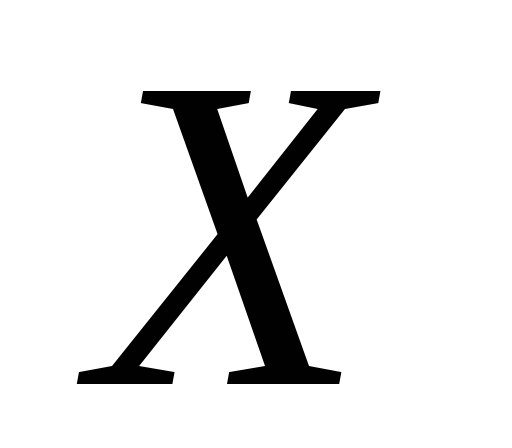 та
та відкрите тоді і тільки тоді, коли
відкрите тоді і тільки тоді, коли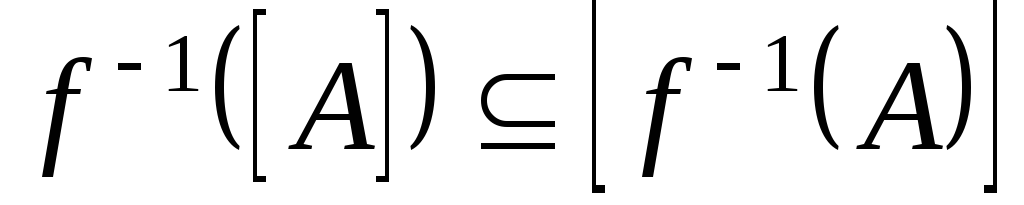 для будь-якої підмножини
для будь-якої підмножини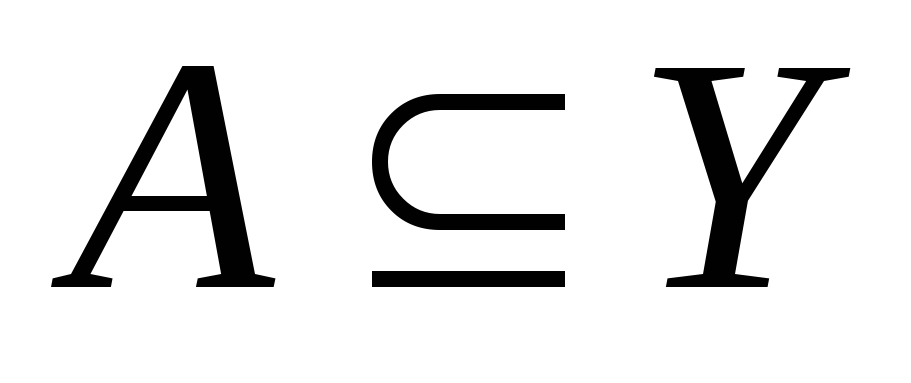 .
.
Варіант 9
Довести, що множина
 ніде не щільна тоді і тільки тоді, коли
в будь-якому околі будь-якої точки існує
точка, що входить разом з деяким своїм
околом в доповнення множини
ніде не щільна тоді і тільки тоді, коли
в будь-якому околі будь-якої точки існує
точка, що входить разом з деяким своїм
околом в доповнення множини
 .
.Навести прямий опис множин скрізь щільних у дискретному просторі та в топології стрілки.
Довести, що якщо простір
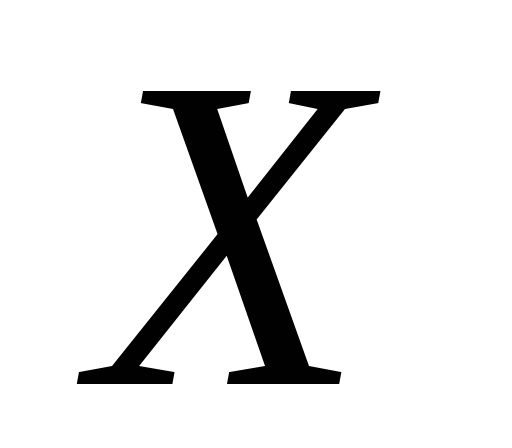 з першою аксіомою зчисленності буде
сепарабельним, то і будь-який скрізь
щільний в
з першою аксіомою зчисленності буде
сепарабельним, то і будь-який скрізь
щільний в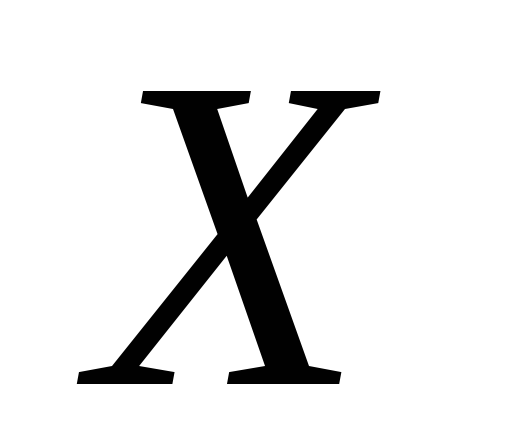 підпростір теж сепарабельний.
підпростір теж сепарабельний.Навести приклад негомеоморфних топологічних просторів, кожний з яких гомеоморфний підпростору іншого.
4.Аксіоми зчисленності та відокремленості. Нормальні простори. Гомеоморфні простори Варіант 1
Нехай
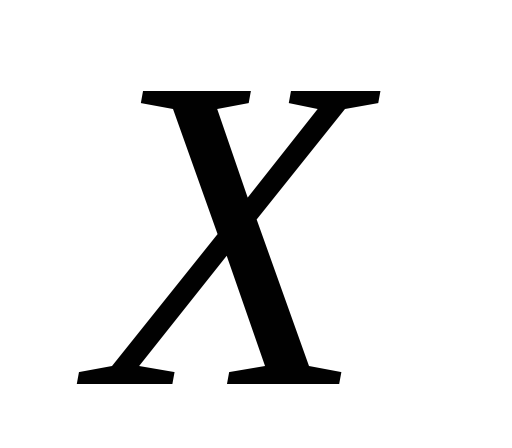 – простір з другою аксіомою зчисленності.
Довести, що з будь-якої бази простору
– простір з другою аксіомою зчисленності.
Довести, що з будь-якої бази простору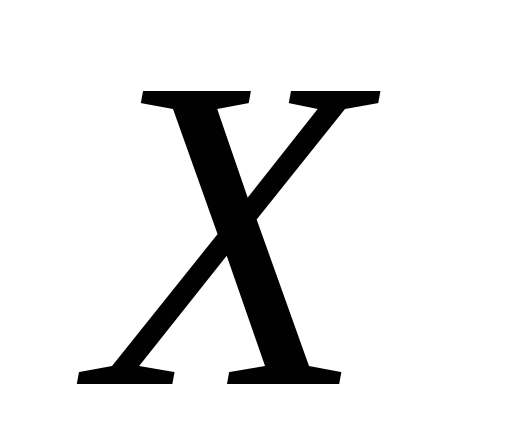 можна виділити зчисленний набір множин,
який також буде базою простору
можна виділити зчисленний набір множин,
який також буде базою простору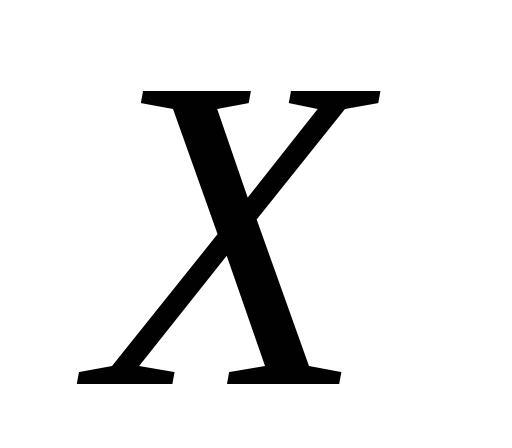 .
.Навести приклад
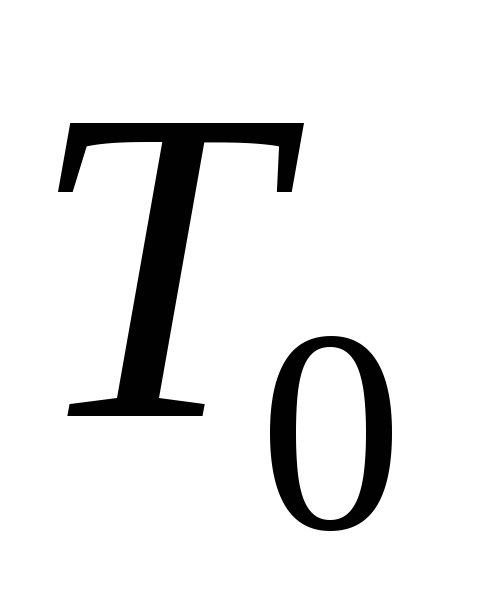 – простору, який не є
– простору, який не є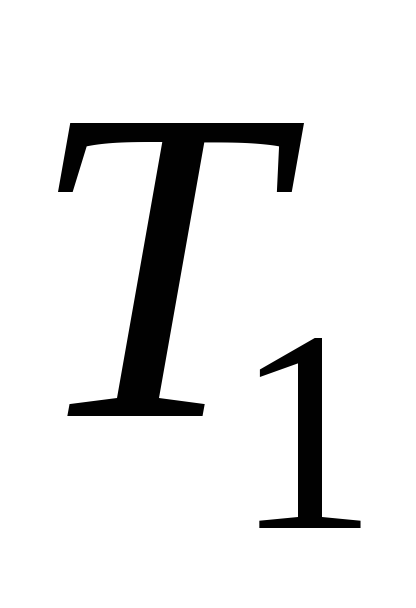 – простором.
– простором.Довести, що замкнений підпростір нормального простору також є нормальним.
Нехай
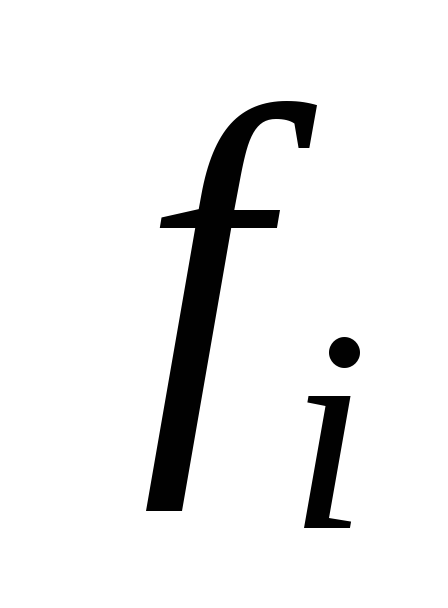 ,
,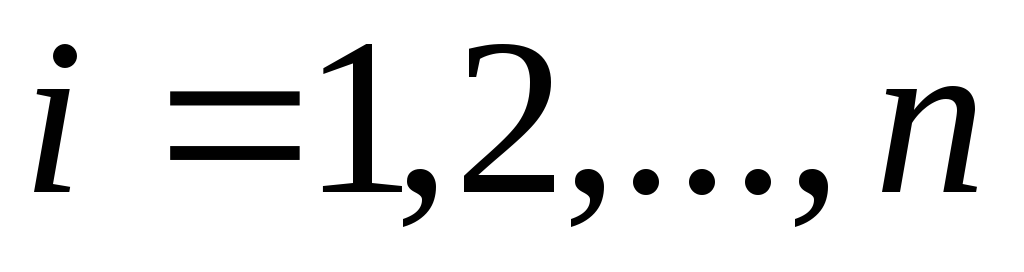 –
неперервні відображення
–
неперервні відображення
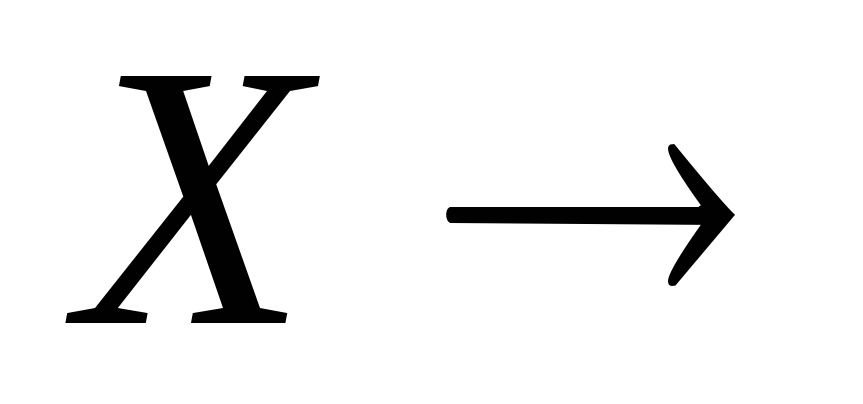
 .
Довести, що підмножина простору
.
Довести, що підмножина простору ,
що складається з усіх розв’язків
системи нерівностей
,
що складається з усіх розв’язків
системи нерівностей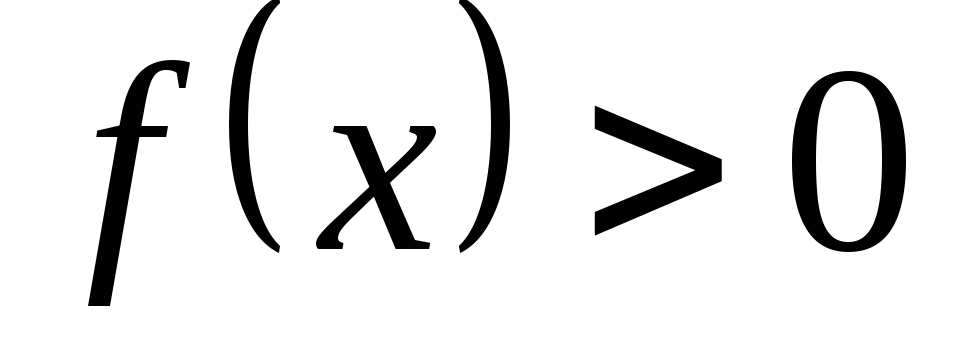 ,
, ,
буде відкритою. Чи можна скінченну
систему замінити нескінченною?
,
буде відкритою. Чи можна скінченну
систему замінити нескінченною?
Варіант 2
Нехай
 – множина дійсних чисел і β – сім’я
всіх інтервалів типу
– множина дійсних чисел і β – сім’я
всіх інтервалів типу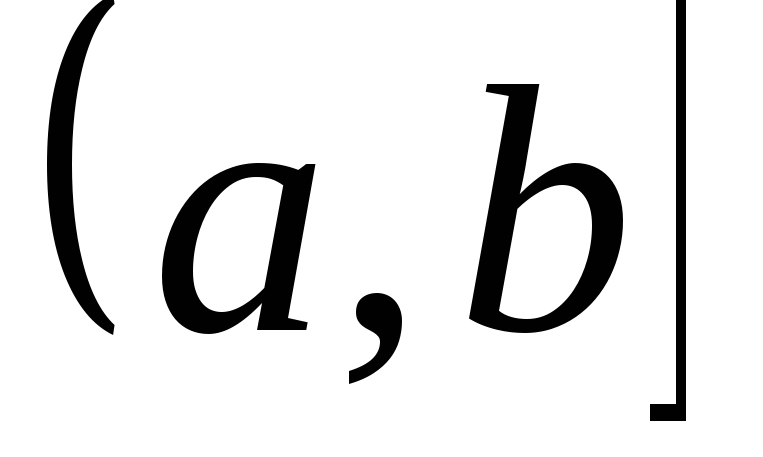 ,
,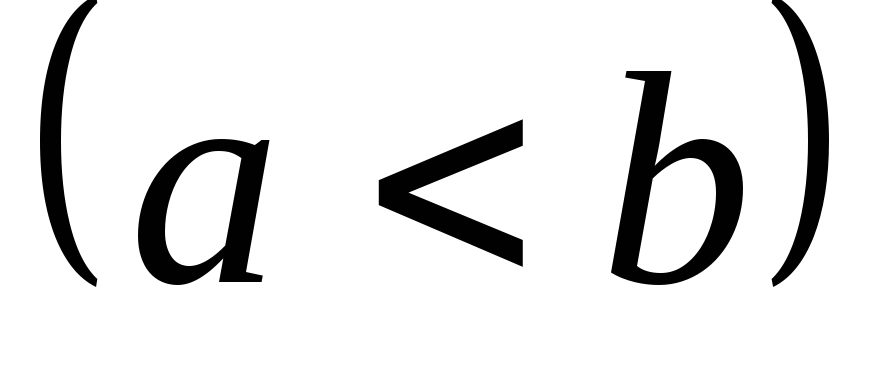 .
Довести, що сім’я β є базою деякої
топології τ і що топологічний простір
.
Довести, що сім’я β є базою деякої
топології τ і що топологічний простір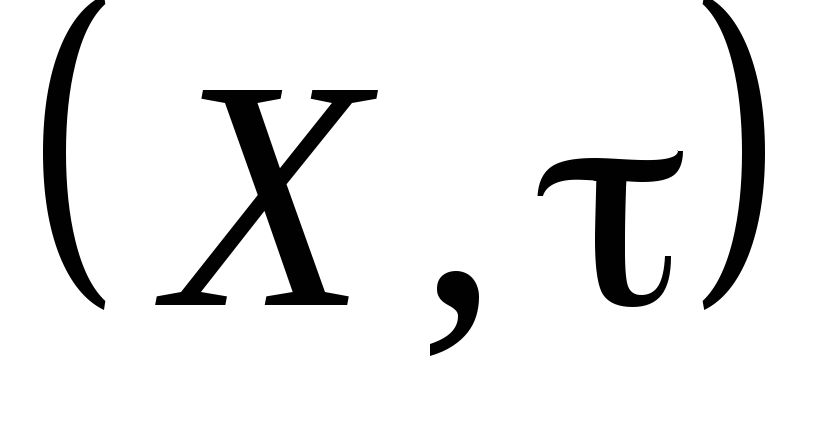 – нормальний неметризований сепарабельний
простір з першою аксіомою зчисленності,
на якому не виконується друга аксіома
зчисленності.
– нормальний неметризований сепарабельний
простір з першою аксіомою зчисленності,
на якому не виконується друга аксіома
зчисленності.Навести приклад негаусдорфового
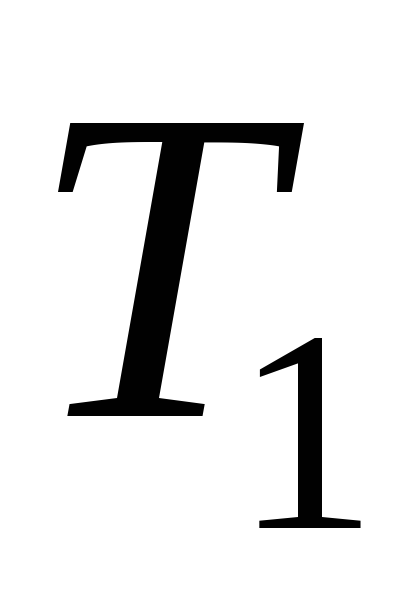 – простору
– просторуНехай
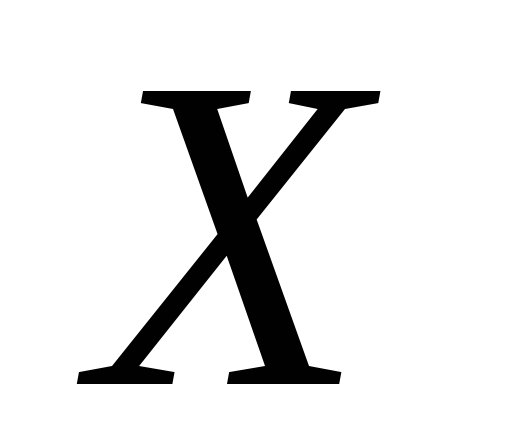 –
гаусдорфів простір, у якому множина
неізольованих точок скінченна. Довести,
що
–
гаусдорфів простір, у якому множина
неізольованих точок скінченна. Довести,
що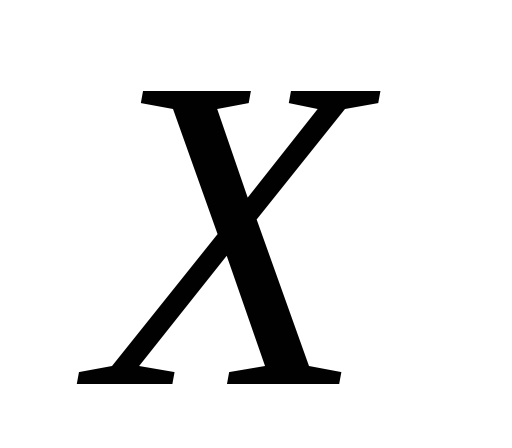 –
нормальний простір.
–
нормальний простір.Побудувати гомеоморфізми між множинами:
а)
![]() та
та![]() ,
,![]() ;
;
б)
![]() та
та![]() ;
;
в)
![]() та
та![]() .
.
Варіант 3
Довести, що
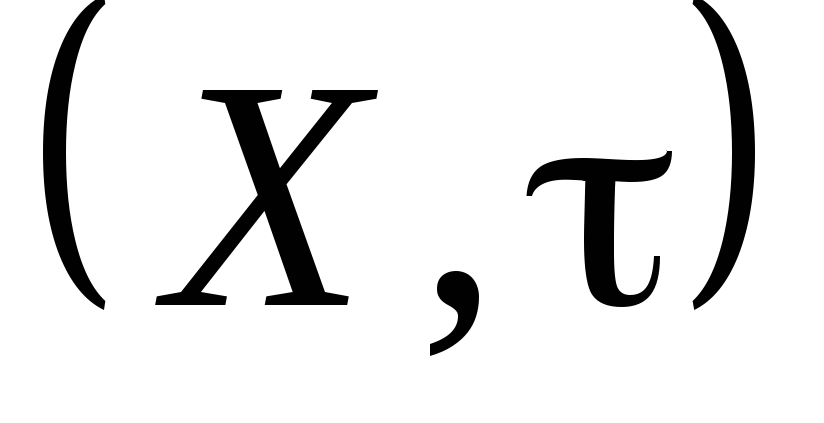 – топологічний простір та вибрати в
ньому дві різні бази, якщо:
– топологічний простір та вибрати в
ньому дві різні бази, якщо:
![]() ,
,
![]() ø,
ø,![]() .
.
Нехай
 і
і – дві різні топології на одній і тій
самій множині
– дві різні топології на одній і тій
самій множині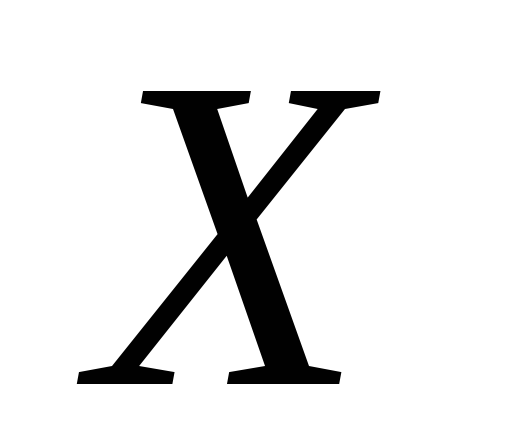 і
і .
Довести, що якщо
.
Довести, що якщо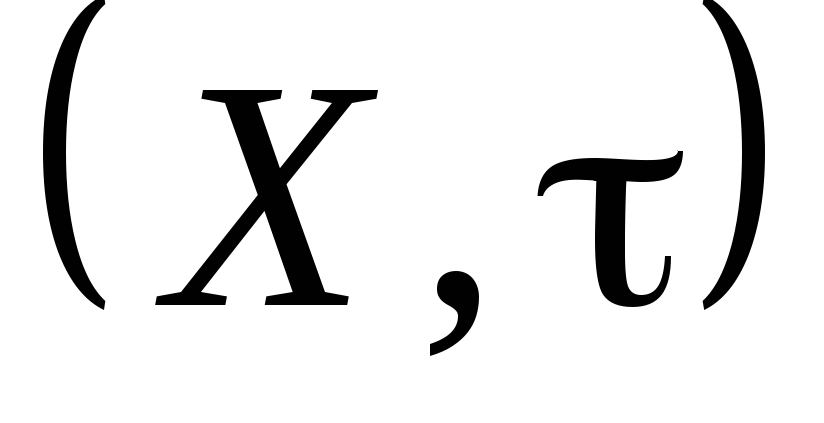 –
–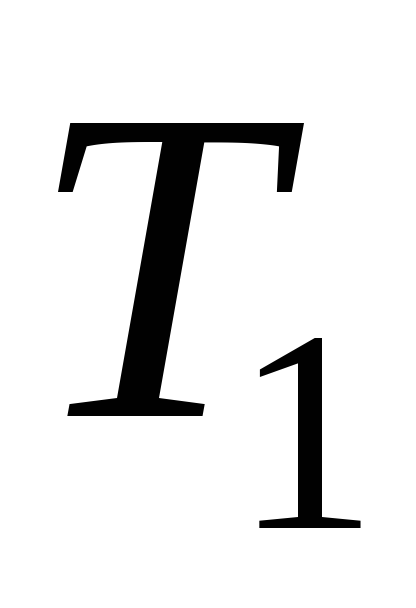 – простір (
– простір (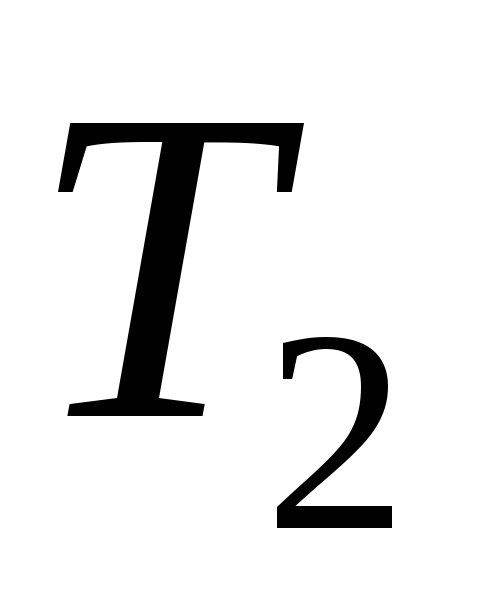 –
простір), тоді
–
простір), тоді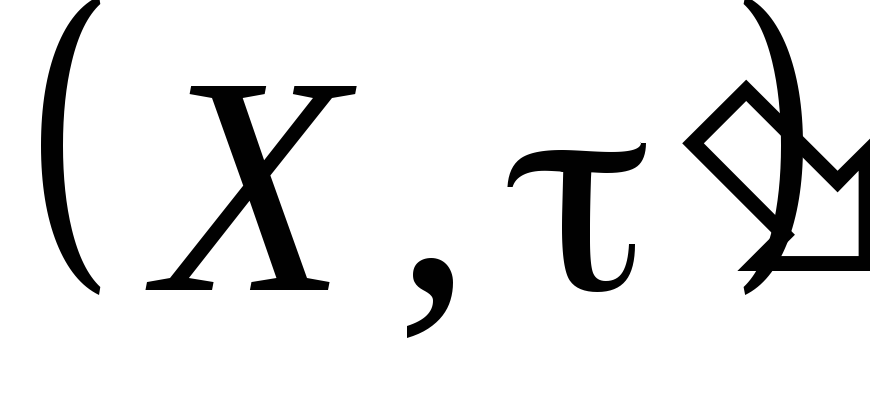 –
–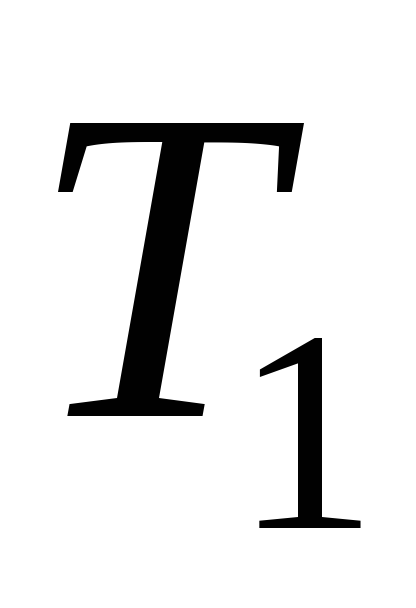 – простір (
– простір (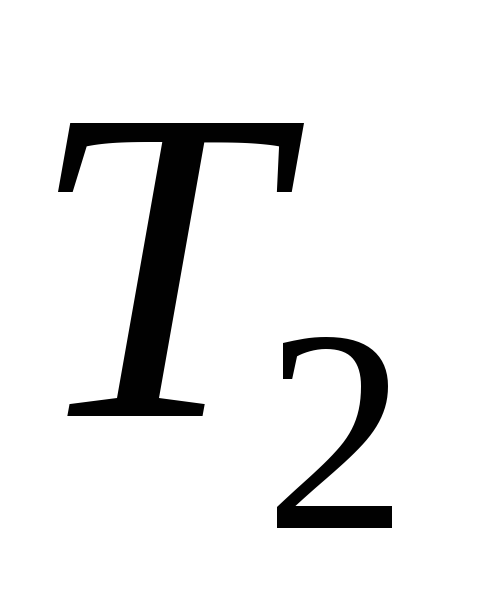 –
простір) .
–
простір) .Довести, що регулярність є спадковою властивістю.
Довести, що простір
 гомеоморфний до будь-якої відкритої
кулі цього простору.
гомеоморфний до будь-якої відкритої
кулі цього простору.
Варіант 4
Довести, що
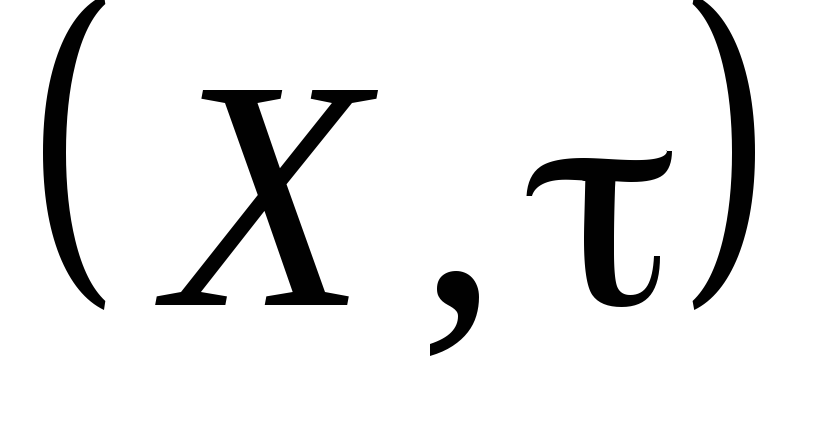 – топологічний простір і вибрати
мінімальну базу, якщо:
– топологічний простір і вибрати
мінімальну базу, якщо:
![]() ,
,
![]() ø,
ø,![]() .
.
Довести, що
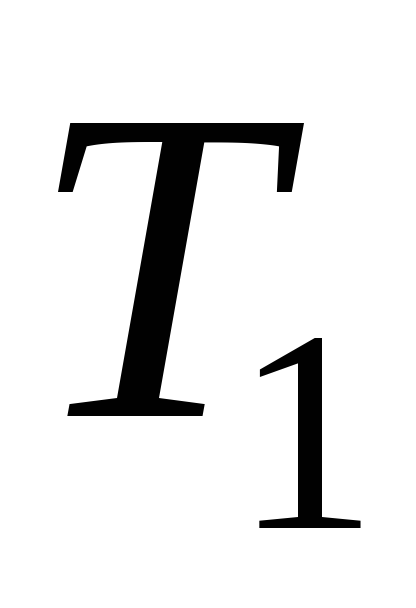 – простір, у якому тільки одна точка
не ізольована, а решта точок – ізольовані,-
нормальний простір.
– простір, у якому тільки одна точка
не ізольована, а решта точок – ізольовані,-
нормальний простір.Довести, що в
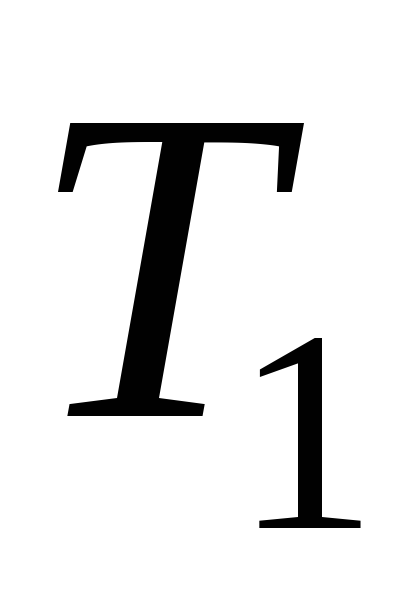 – просторі множина всіх граничних
точок будь-якої підмножини замкнена.
– просторі множина всіх граничних
точок будь-якої підмножини замкнена.Нехай
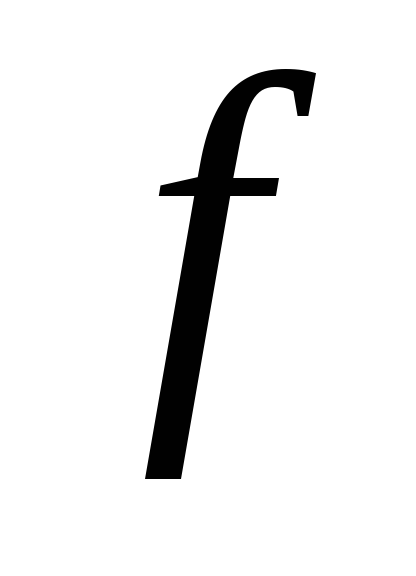 і
і – такі неперервні відображення
топологічного простору
– такі неперервні відображення
топологічного простору в гаусдорфів простір
в гаусдорфів простір ,
що множина
,
що множина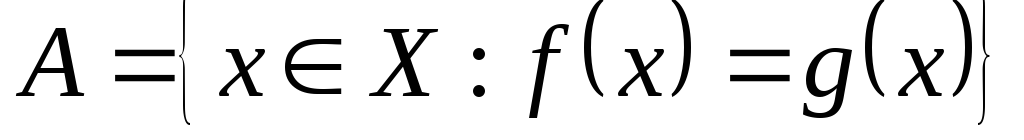 скрізь щільна в
скрізь щільна в .
Довести, що
.
Довести, що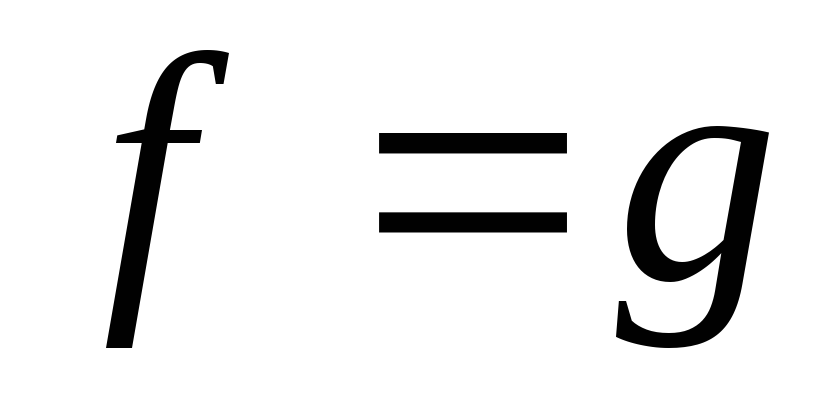 на всьому просторі
на всьому просторі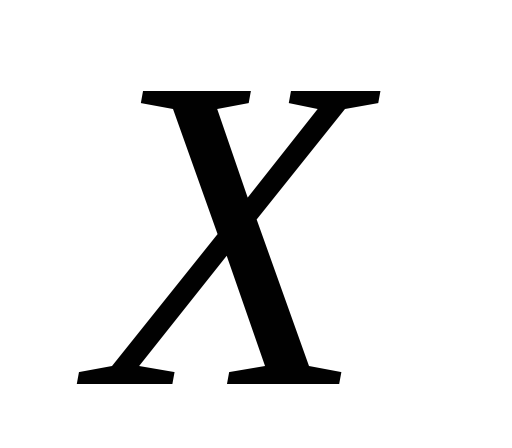 .
.
