
- •Практикум з курсу
- •Метричні й топологічні простори Варіант 1
- •Варіант 2
- •Варіант 3
- •Варіант 4
- •Варіант 5
- •Варіант 6
- •Варіант 7
- •Варіант 8
- •Варіант 9
- •Скрізь щільні та ніде не щільні множини. Сепарабельні простори. Неперервні відображення Варіант 1
- •Варіант 2
- •Варіант 3
- •Варіант 8
- •Варіант 9
- •4.Аксіоми зчисленності та відокремленості. Нормальні простори. Гомеоморфні простори Варіант 1
- •Варіант 2
- •Варіант 3
- •Варіант 4
- •Варіант 5
- •Варіант 6
- •Варіант 7
- •Варіант 7
- •Варіант 4
- •Список рекомендованої літератури
УДК 514.12 (075.8)
Т61
Рецензенти: канд. фіз.-мат. наук, доц. Є.М. Іщенко
канд. фіз.-мат. наук, доц. Л.І. Бойко
Т61 Тушев, А.В. Практикум з курсу „Топологія” [Текст] / А.В. Тушев; Н.А. Турбай . – Д.: РВВ ДНУ, 2013. – 16 с.
Наведені практичні завдання з базових розділів курсу „Топологія”.
Для студентів механіко-математичного факультету ДНУ.
Темплан 2012, поз.
Навчальне видання
Анатолій Володимирович Тушев
Надія Анатоліївна Турбай
Практикум з курсу
„Топологія”
Редактор А.Я. Пащенко
Техредактор Л.П. Замятіна
Коректор Т.А. Белиба
Підписано до друку .05.2013. Формат 60x84/16. Папір друкарський.
Друк плоский. Ум.друк.арк. . Ум.фарбовідб. . Обл.-вид.арк. .
Тираж 100 пр. Зам. № .
РВВ ДНУ, пр. Гагаріна, 72, м. Дніпропетровськ, 49010.
Друкарня ДНУ, вул. Наукова, 5, м. Дніпропетровськ, 49050.
© Тушев А.В., Турбай Н.А., 2013
Метричні й топологічні простори Варіант 1
Довести, що множина всіх неперервних на
 функцій складає метричний простір,
якщо під відстанню між двома елементами
функцій складає метричний простір,
якщо під відстанню між двома елементами та
та цієї множини розуміти число
цієї множини розуміти число
![]() .
.
Нехай
 і
і - дві метрики на множині
- дві метрики на множині .
Довести, що якщо існують сталі
.
Довести, що якщо існують сталі та
та такі, що
такі, що
![]() ,
,
![]()
то
метрики
![]() та
та![]() еквівалентні.
еквівалентні.
Нехай
 .
Визначити, які з наступних наборів його
підмножин є топологічними структурами
на множині
.
Визначити, які з наступних наборів його
підмножин є топологічними структурами
на множині :
:
а)
![]() ,
,![]()
б)
![]() ,
,![]()
в)
![]() ,
,![]()
Якщо який-небудь з наборів а) – в) виявиться топологією, то знайти сім’ю замкнених множин для цих топологій.
Довести, що
 .
.
Варіант 2
Визначити, чи є метричним простором множина всіх дійсних чисел, якщо під відстанню між двома числами
 та
та розуміти число
розуміти число
![]()
Довести, що метрики
 і
і ,
задані на множині
,
задані на множині ,
еквівалентні.
,
еквівалентні.Нехай
 – промінь
– промінь ,
а
,
а складається з
складається з ,
,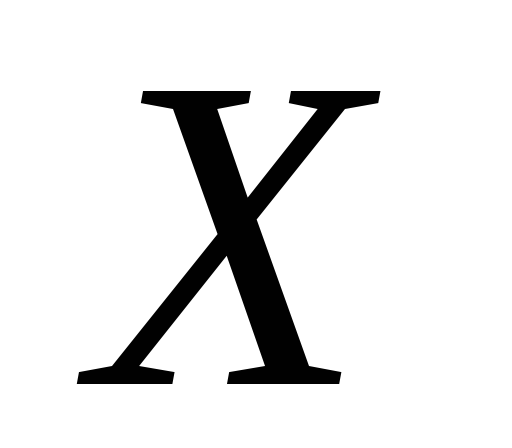 і всіх можливих променів
і всіх можливих променів ,
де
,
де .
Визначити, чи є
.
Визначити, чи є топологією на
топологією на .
Якщо так, знайти сім’ю
замкнених множин.
.
Якщо так, знайти сім’ю
замкнених множин.Довести, що
 .
.
Варіант 3
Визначити, чи буде метричним простором множина дійсних чисел, якщо метрику
 на ній означити так:
на ній означити так:
![]() .
.
Довести, що метрики
 і
і – еквівалентні на множині
– еквівалентні на множині .
.Нехай
 – числова пряма,
– числова пряма, складається з
складається з ,
, і всіх можливих променів вигляду
і всіх можливих променів вигляду ,
де
,
де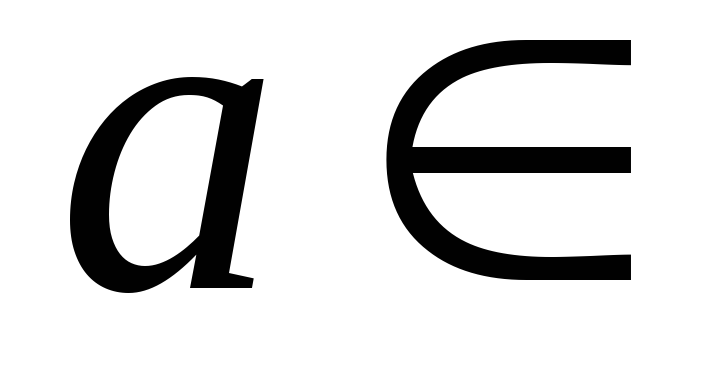
 .
Визначити, чи буде
.
Визначити, чи буде топологією на
топологією на .
Якщо так, знайти сім’ю
замкнених множин.
.
Якщо так, знайти сім’ю
замкнених множин.Довести, що
 .
.
Варіант 4
1. Довести,
що функція
![]()
![]() +
(
+
(![]() +–
множина невід’ємних дійсних чисел)
є
метрикою
на
+–
множина невід’ємних дійсних чисел)
є
метрикою
на
![]() тоді і тільки тоді, коли виконуються
такі умови:
тоді і тільки тоді, коли виконуються
такі умови:
а)
![]()
![]()
![]() ;
;
б)
![]() ,
,![]() .
.
2.
Довести, що метрики
![]() і
і![]() еквівалентні на множині .
еквівалентні на множині .
3. Нехай
![]() – нескінченна множина, а
– нескінченна множина, а![]() – топологія скінчених доповнень на
– топологія скінчених доповнень на![]() .
Довести аксіоми відкритих множин. Знайти
сім’ю
замкнених множин.
.
Довести аксіоми відкритих множин. Знайти
сім’ю
замкнених множин.
4. Довести,
що
 .
.
Варіант 5
Довести, що функція

 +
(
+
( +–
множина невід’ємних дійсних чисел) є
функцією, яка задовольняє умовам:
+–
множина невід’ємних дійсних чисел) є
функцією, яка задовольняє умовам:
а)
![]()
![]()
![]() ;
;
б)
![]() ,
,![]()
то
функція
![]() буде метрикою на
буде метрикою на![]() .
.
Довести, що метрики
 і
і еквівалентні на множині .
еквівалентні на множині .Визначити, чи буде перетин топологій, які задані на одній і тій самій множині
 ,
топологією на
,
топологією на .
.Довести, що
 ,
, –
відображення і
–
відображення і .
.
Варіант 6
Довести, що якщо
 і
і – метрики на
– метрики на ,
то
,
то і
і також є метриками на
також є метриками на .
Чи будуть метриками функції
.
Чи будуть метриками функції ;
; ;
; ?
?Довести, що метрики
 і
і еквівалентні на множині
еквівалентні на множині .
.Визначити, чи буде об’єднання топологій, які задані на одній і тій самій множині
 ,
топологією на
,
топологією на .
.Довести, що
 ,
, –
відображення і
–
відображення і .
.
Варіант 7
Довести, що коли
 – метрика на
– метрика на ,
то функція
,
то функція також є метрикою, якщо
також є метрикою, якщо задовольняє
умовам
задовольняє
умовам
 ,
монотонно зростає і
,
монотонно зростає і
![]() ,
,
![]()
![]() .
.
Показати, що метрики
 і
і (див. задачу 1) еквівалентні, якщо
(див. задачу 1) еквівалентні, якщо – неперервна функція.
– неперервна функція.Нехай
 –
площина. Визначити, чи буде топологічною
структурою набір множин, що складається
з
–
площина. Визначити, чи буде топологічною
структурою набір множин, що складається
з ,
, і відкритих кругів з центром в одній і
тій самій точці з різноманітними
радіусами.
і відкритих кругів з центром в одній і
тій самій точці з різноманітними
радіусами.Довести, що
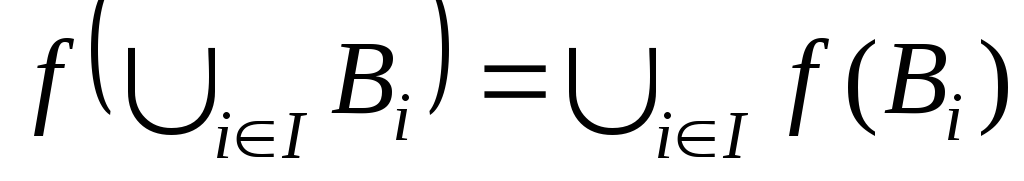 ,
, –
відображення і
–
відображення і .
.
Варіант 8
Нехай
 – метрика на
– метрика на .
Довести, що функція
.
Довести, що функція також є метрикою.
також є метрикою.Довести, що метрики
 і
і (див. задачу 1) еквівалентні.
(див. задачу 1) еквівалентні.Нехай

 і
і

 ,
, ,
де
,
де .
Визначити, чи буде
.
Визначити, чи буде топологією на множині
топологією на множині
 .
Якщо так, то навести опис сім’ї
замкнених
множин.
.
Якщо так, то навести опис сім’ї
замкнених
множин.Довести, що
 ,
, –
відображення і
–
відображення і .
.
Варіант 9
Нехай
 – метричний простір і
– метричний простір і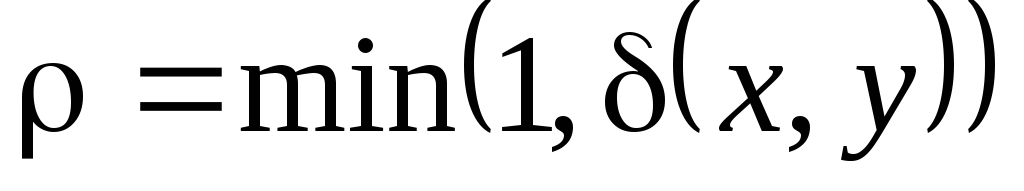 .
Довести, що
.
Довести, що – метрика на
– метрика на .
.Довести, що метрики
 та
та з задачі 1 еквівалентні.
з задачі 1 еквівалентні.Знайти число різних топологій на множині з трьох елементів. Навести опис сім’ї замкнених множин цих топологій.
Навести приклад, коли
 ,
де
,
де –
відображення і
–
відображення і .
.
Замкнені множини. Ізольовані, граничні, межові точки множин
Варіант 1
Знайти всі граничні, межові, ізольовані та внутрішні точки множин, що належать
 :
:
а)![]() ;
;
б)![]()
![]()
![]() (
(![]() \
\![]() )
)![]()
![]() .
.
Ці множини є відкритими чи замкненими?
Знайти замикання множин усіх точок вигляду
 ,
де
,
де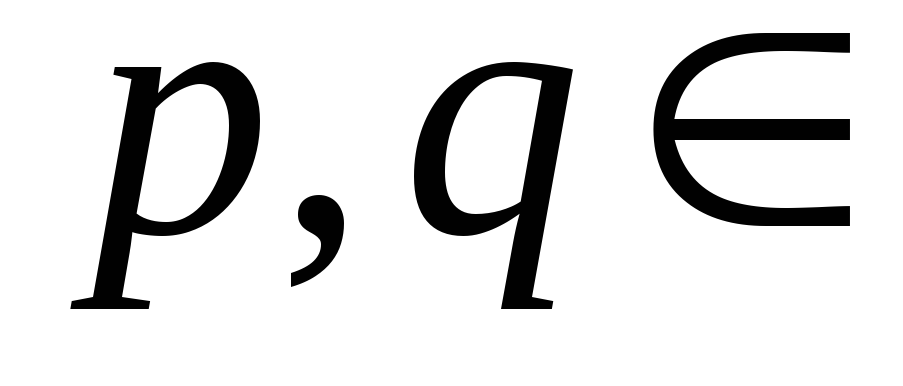
 .
.Навести опис топологічної структури, замкнених множин і околи точок, що індукуються в множині
 топологією прямої
топологією прямої .
.Нехай множина
 відкрита в топологічному просторі
відкрита в топологічному просторі і
і
 ,
де
,
де .
Довести, що
.
Довести, що
 .
.Нехай
 – підмножина метричного простору.
Відомо, що
– підмножина метричного простору.
Відомо, що .
Довести, що
.
Довести, що не має граничних точок.
не має граничних точок.
Варіант 2
Знайти всі граничні, межові, ізольовані та внутрішні точки множин:
а)![]() (
(![]()
![]()
![]() ;
б)
;
б)![]()
![]() де
де![]()
![]()
![]() .
.
Ці множини є відкритими чи замкненими?
Знайти замикання множини всіх точок вигляду
 ,
де
,
де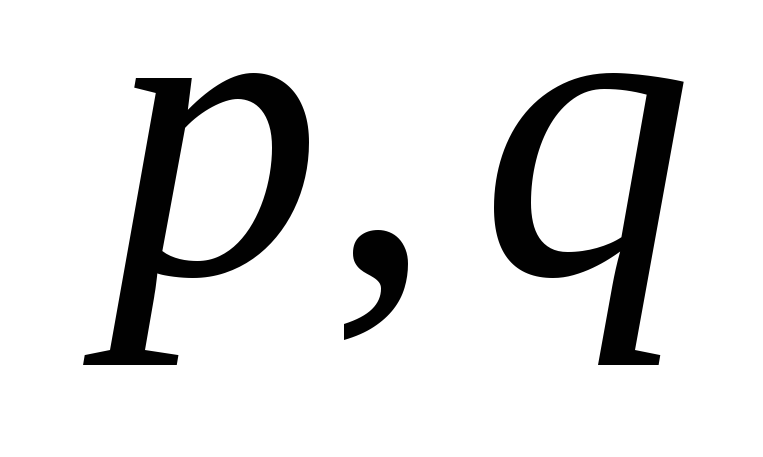 – усі можливі цілі числа, відмінні від
нуля.
– усі можливі цілі числа, відмінні від
нуля.Описати топологічну структуру
 ,
що індукована в
,
що індукована в топологією стрілки. (простір із задачі
3 варіанта
2 лабораторної роботи 1 називається
стрілкою). Описати в топологічному
просторі (
топологією стрілки. (простір із задачі
3 варіанта
2 лабораторної роботи 1 називається
стрілкою). Описати в топологічному
просторі ( ,
, )
сім’ю
замкнених множин околів точки.
)
сім’ю
замкнених множин околів точки.Нехай множина
 –
замкнена, а множина
–
замкнена, а множина –
відкрита. Довести, що
–
відкрита. Довести, що – замкнена,
– замкнена, –
відкрита.
–
відкрита.Нехай

 – множина вигляду
– множина вигляду ,
де
,
де пробігають усі натуральні числа.
Визначити, чи буде множина
пробігають усі натуральні числа.
Визначити, чи буде множина замкненою. Яка у неї похідна множина?
Якими будуть друга та третя похідні
множини?
замкненою. Яка у неї похідна множина?
Якими будуть друга та третя похідні
множини?
