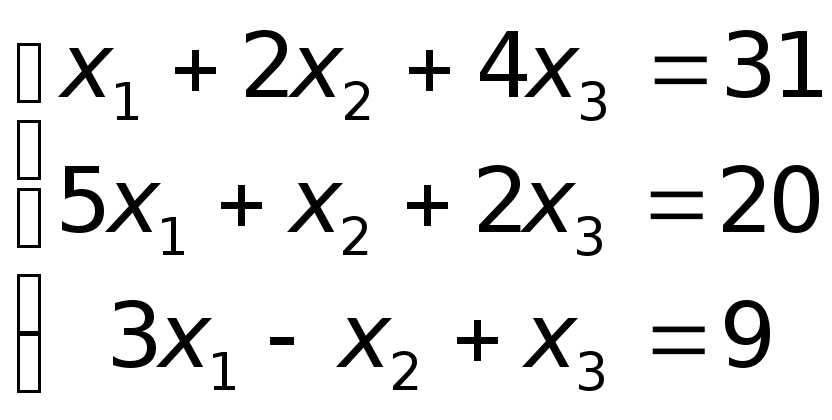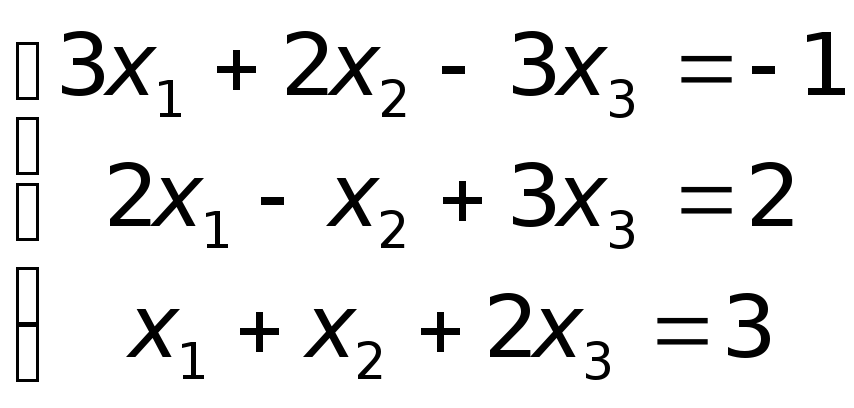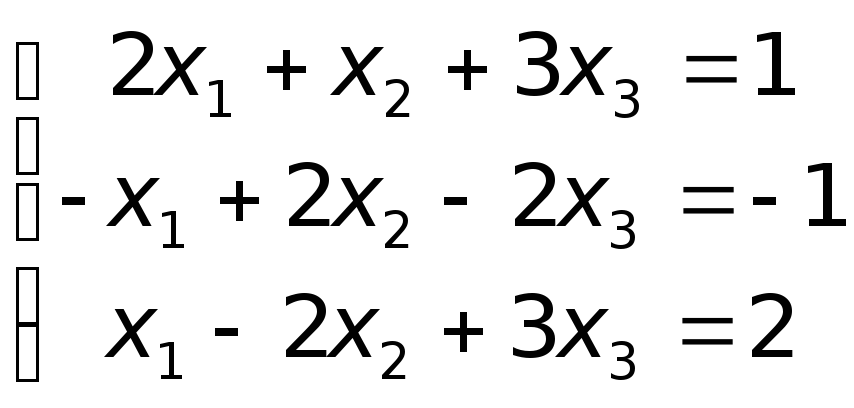5.Примеры для самостоятельного решения.

3. Решить неравенство

5. Определить при каких a и b система имеет:

1. единственное решение;

2. бесконечное множество решений;

3. не имеет решений

6.Компьютерное практическое задание №1

Задана система 3-х линейных уравнений с 3-мя неизвестными

Найти решение заданной системы уравнений следующими способами

Для этого составим основную матрицу М1 и расширенную матрицу М2

Вычислим ранги матрицы М1 и матрицы М2

Так как, ранги основной матрицы М1 и расширенной матрицы М2 равны, то, согласно теореме Кронекера - Капелли, заданная система уравнений совместна и имеет единственное решение.

Введя матрицы М1, Х, М3 заданную систему уравнений можно представить в матричной форме

Умножая последнее равенство на- матрицу обратную к матрице, получаем решение заданной системы уравнений в матричной форме

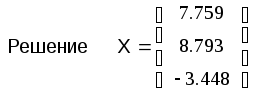
(B) Решение заданной системы уравнений с помощью

операторов GIVEN и FIND

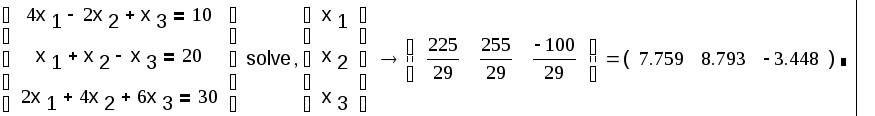
1. Индивидуальные задания по теме

«Элементы линейная алгебра».

Дана система уравнений:

Проверить её на совместность и решить следующими способами:

1		11
2		12
3		13
4		14
5		15
6		16
7		17
8		18
9		19
10		20

8.Литература

1. Курош А.Г. Курс высшей алгебры. 11-е изд., М., 1975

2. Мальцев А.И. Основы линейной алгебры. 4-е изд., М., 1975

3. Ильин В.А., Позняк Э.Г. Линейная алгебра. 3-е изд., М., 1984

4. Щипачев В.С. Задачник по высшей математике. М.: Высшая школа,2001

Начало документа