
Пешат И.В.
-
Тема. Элементы линейной алгебры
Вступление.
Матрицы.
Определители.
Системы линейных уравнений.
Примеры для самостоятельного решения.
Компьютерное практическое занятие №1.
Индивидуальные задания по теме “Элементы линейной алгебры”.
Литература.
Вступление.
Матричный язык, обозначения и матричные вычисления широко используются в различных областях современной математики и ее приложений. Матрицы являются основным математическим аппаратом линейной алгебры и применяются при исследовании линейных отображений векторных пространств, линейных и квадратичных форм, систем уравнений. Матрицы используются в математическом анализе при интегрировании систем дифференциальных уравнений, в механике и электротехнике при исследовании малых колебаний механических и электрических систем, в теории вероятностей, в квантовой механике.
Историческая справка.
Впервые матрица как математическое понятие появилась в работах Уильямса Гамильтона (Hamilton William Rowan, 4.8.1805, Дублин – 2.9.1865, Даисинк, ирландский математик и астроном); Артура Кэли (Cayley Arthur, 16.8.1821, Ричмонд – 26.1.1895, английский математик) и Джеймса Сильвестра (Sylvester James Joseph, 3.9.1814, Лондон – 15.3.1897, Лондон, английский математик в середине 19в.)
Основы Теории Матриц созданы К. Вейерштрассом и Г. Фробениусом во 2-й половине 19в и начале 20в.
Современные обозначения – две вертикальные черточки – ввел А. Кэли (1841).
2. Матрицы.
2.1. Основные определения (часть первая)
Определение 1. Матрицей называется прямоугольная таблица M, образованная из элементов некоторого множества, и состоящая из m-строк и n‑столбцов;
m x n- размерность матрицы.
 (1),
(1),
или сокращенная
запись![]()
Определение 2. Если в матрице М, количество строк m равно количеству столбцов n, то такая матрица называется квадратной, и n-порядок матрицы.
 (2)
(2)
или сокращенная
запись .
.
Определение 3. Матрица, состоящая из одной строки, называется матрицей ‑ строкой,
или вектор ‑ строкой.
![]() (3)
(3)
Определение 4. Матрица, состоящая из одного столбца, называется матрицей ‑ столбцом, или вектор ‑ столбцом.
 (4)
(4)
Определение 5.
Матрица
![]() называется равной
матрице
называется равной
матрице
![]() ,
,
если
они одинакового размера и
![]() .
.
2.2. Операции над матрицами.
Определение 1.
Алгебраической
суммой
прямоугольных матриц
![]() и
и![]() ,
,
одного
размера m
x
n,
называется матрица
![]() ,
такого же размера
,
такого же размера
m
x
n,
для которой выполняется условие![]()
![]() .
.
![]() Пример
№1.
Дано:
Пример
№1.
Дано: 
Найти: С = A + B.
Решение
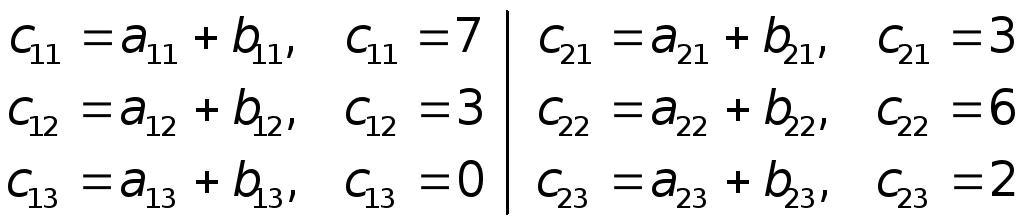
Ответ:
 .
.
Определение
2.
Произведением
матрицы
![]() на
число k
называется матрица
D
такого же размера m
x
n,
для которой выполняется условие
на
число k
называется матрица
D
такого же размера m
x
n,
для которой выполняется условие
d = kaij .

Пример №2.
Дано:
Вычислить: D = k A .
Решение.
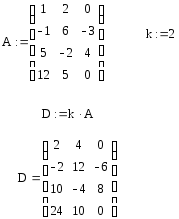
Определение 3.
Произведением
матрицы
![]() ,
размерностиmxn
и
,
размерностиmxn
и
![]()
размерности
n
x
s
на называется матрица
![]() ,
размера m
x
s,
,
размера m
x
s,
такая
что
![]() .
.
Правило умножения матриц называют правилом умножения
строки на столбец.
![]() Пример
№3
Пример
№3
Д
- размерность
матрица А: (3x4)
- размерность
матрица B:
(4x5)
Количество столбцов матрицы А равно количеству строк матрицы В, следовательно,
эти матрицы можно перемножить. Полученная матрица С будет размерностью (3x5).
Найти С = AB
Ответ:
2.3. Свойства операций над матрицами.
Операции сложения (вычитания) матриц и умножения матрицы на число обладают следующими свойствами:
A + B = B + A;
(A + B) + C = A + (B + C);
k(A +B) = kA + kB;
(k1 + k2)A = k1A + k2A;
k1(k2A) = (k1k2)A = k2(k1A)
Операция умножения матриц обладает следующими свойствами:
(AB)C = A(BC);
(A+B)C = AC+BC или A(B+C) = AB+AC;
k(AB) = A(kB) = (kA)B.
но: AB BA, т.е. произведение матриц не коммутативно.
Определение.
Если для матриц
![]() и
и![]() выполняется условиеAB = BA,
выполняется условиеAB = BA,
то матрицы A и B называются перестановочными.
2.4. Основные определения (часть вторая)
Определение 6. Матрица AT называется транспонированной, если она получена из
матрицы А путем замены строк столбцами.
 ;
;
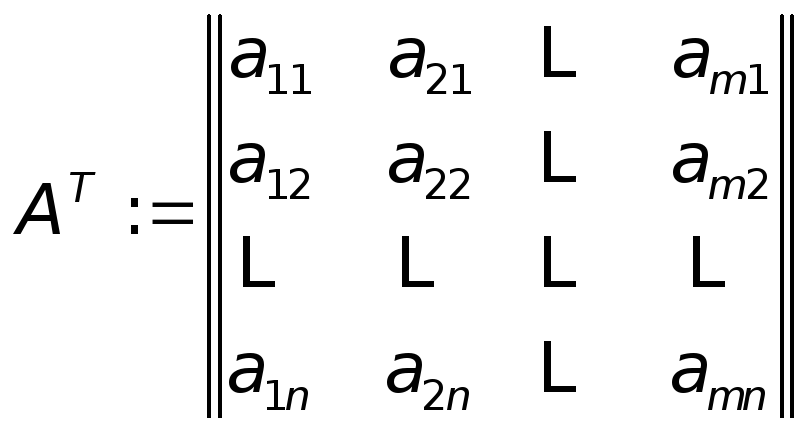 (5)
(5)
Операция транспонирования обладает свойствами:
1. (A+B)T = AT +BT 4. (AB)T = BT AT;
2. (k A)T = k AT 5. Det AT = det A.
3. (AT)T = A;
Определение 7.
Квадратная
матрица
![]() ,
у которой все элементы, расположенные
,
у которой все элементы, расположенные
вне главной диагонали, равны 0, называется диагональной
и
обозначается
![]() .
.
Определение 8. Если в диагональной матрице, все элементы, стоящие на главной диагонали,
равны 1, то такая матрица называется единичной иобозначается
 .
(6)
.
(6)
Для единичной матрицы справедливо следующее свойство:
Пусть матрица А имеет размерность m x n. Тогда AEn = A и EmA = A.
