1. , 4.,

2., 5.,

3., 6..

В интегралах 1-3 качествеu принимают. Тогда, послеn-кратного применения формулы (19) придем к одному из табличных интегралов

, ,.

В интегралах 4-6 при дифференцировании упроститься трансцендентный множитель,или, который следует принять заu.

Вычислить следующие интегралы.

Пример 7.

Пример 8.

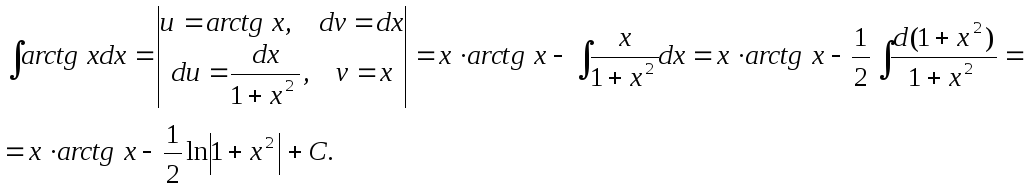
Приведение интегралов к самому себе

Если подынтегральная функция имеет вид:

,,и так далее,

то после двукратного интегрирования по частям получим выражение, содержащее исходный интеграл :

,

где - некоторая постоянная.

Разрешая полученное уравнение относительно , получим формулу для вычисления исходного интеграла:

.

Этот случай применения метода интегрирования по частям называется «приведение интеграла к самому себе».

Пример 9. Вычислить интеграл .

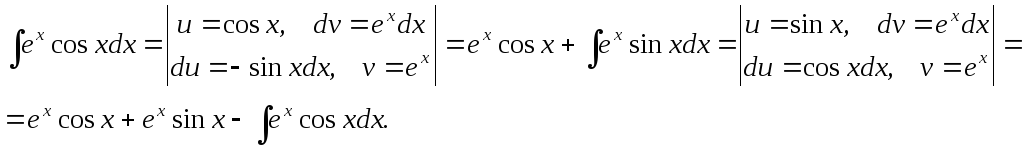
В правой части стоит исходный интеграл . Перенеся его в левую часть, получим:

.

Пример 10. Вычислить интеграл .

Отсюда: .

4.5. Интегрирование простейших правильных рациональных дробей

Определение. Простейшими правильными дробями I, II и III типов называются следующие дроби:

I. ;

II. ; (- целое положительное число);

III.; (корни знаменателя комплексные, то есть:.

Рассмотрим интегралы от простейших дробей.

I. ; (20)

II. ; (21)

III. ;

Преобразуем числитель дроби таким образом, чтобы выделить в числителе слагаемое , равное производной знаменателя.

= .

Рассмотрим первый из двух полученных интегралов и сделаем в нем замену:

.

Во втором интеграле дополним знаменатель до полного квадрата:

Окончательно, интеграл от дроби третьего типа равен:

=+. (22)

Таким образом, интеграл от простейших дробей I-го типа выражается через логарифмы,II–го типа – через рациональные функции,III-го типа – через логарифмы и арктангенсы.

4.6.Интегрирование дробно-рациональных функций

Одним из классов функций, которые имеют интеграл, выраженный через элементарные функции, является класс алгебраических рациональных функций, то есть функций, получающихся в результате конечного числа алгебраических операций над аргументом.

Всякая рациональная функция может быть представлена в виде отношения двух многочленови:

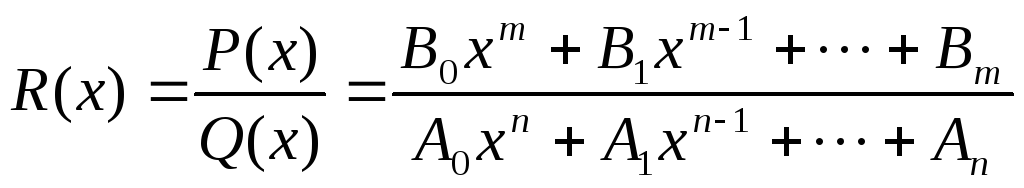. (23)

Будем предполагать, что многочлены не имеют общих корней.

Дробь вида (23) называется правильной, если степень числителя меньше степени знаменателя, то есть,m<n. В противном случае –неправильной.

Если дробь неправильная, то, разделив числитель на знаменатель (по правилу деления многочленов), представим дробь в виде суммы многочлена и правильной дроби:

, (24)

где - многочлен,- правильная дробь, причем степень многочлена- не выше степени (n-1).

Пример.

Так как интегрирование многочлена сводится к сумме табличных интегралов от степенной функции, то основная трудность при интегрировании рациональных дробей заключается в интегрировании правильных рациональных дробей.

В алгебре доказано, что всякая правильная дробь разлагается на сумму рассмотренных вышепростейшихдробей, вид которых определяется корнями знаменателя.

Рассмотрим три частных случая. Здесь и далее будем считать, что коэффициент при старшей степени знаменателяравен единице=1, то естьмногочлен приведенный.

Случай 1. Корни знаменателя, то есть, корниуравнения=0, действительны и различны. Тогда знаменатель представим в виде произведения линейных множителей:

, (25)

а правильная дробь разлагается на простейшие дроби I-готипа:

, (26)

где – некоторые постоянные числа, которые находятся методом неопределенных коэффициентов.

Для этого необходимо:

1. Привести правую часть разложения (26) к общему знаменателю.

2. Приравнять коэффициенты при одинаковых степенях тождественных многочленов, стоящих в числителе левой и правой частей. Получим систему линейных уравнений для определения .

3. Решить полученную систему и найти неопределенные коэффициенты .

Тогда интеграл дробно-рациональной функции (26) будет равен сумме интегралов от простейших дробей I-готипа, вычисляемых по формуле (20).

Пример. Вычислить интеграл.

Решение. Разложим знаменатель на множители, используя теорему Виета:

.

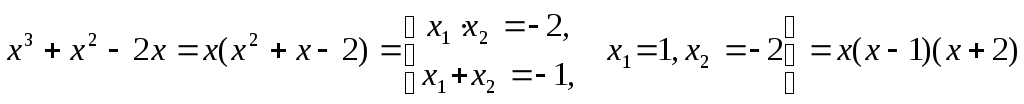Тогда, подынтегральная функция разлагается на сумму простейших дробей:

.

Приведем правую часть к общему знаменателю и приравняем многочлены, стоящие в числителях левой и правой части:

.

. (27)

В правой части приведем подобные при одинаковых степенях х:

Запишем систему трех уравнений для нахождения . Для этого приравняем коэффициенты при одинаковых степеняххв левой и правой частях:

.

Укажем более простой способ нахождения неопределенных коэффициентов, называемый методом частных значений.

Полагая в равенстве (27) получим, откуда. Полагаяполучим. Наконец, полагаяполучим.

Тогда

.

Случай 2. Корня знаменателядействительны, но среди них есть кратные (равные) корни. Тогда знаменатель представим в виде произведения линейных множителей, входящих в произведение в той степени, какова кратность соответствующего корня:

, (28)

где .

Правильная дробь будет разлагаться сумму дробейI–го иII-го типов. Пусть, например,- корень знаменателя кратностиk, а все остальные (n-k) корней различны.

Тогда разложение будет иметь вид:

. (29)

Аналогично, если существуют другие кратные корни. Для некратных корней в разложение (28) входят простейшие дроби первого типа.

Пример. Вычислить интеграл.

Решение. Представим дробь в виде суммы простейших дробей первого и второго рода с неопределенными коэффициентами:

.

Приведем правую часть к общему знаменателю и приравняем многочлены, стоящие в числителях левой и правой части:

.

В правой части приведем подобные при одинаковых степенях х:

Запишем систему четырех уравнений для нахождения и. Для этого приравняем коэффициенты при одинаковых степеняххв левой и правой части

.

Тогда

Случай 3. Среди корней знаменателяесть комплексные однократные корни. То есть, в разложение знаменателя входят множители второй степени, не разложимые на действительные линейные множители, причем они не повторяются.

Тогда в разложении дроби каждому такому множителю будет соответствовать простейшая дробь IIIтипа. Линейным множителям соответствуют простейшие дробиI–го иII-го типов.

Пример. Вычислить интеграл.

Решение. .

.

.

.

13