4.2. Линейная подстановка (метод введения нового аргумента)

Пусть - первообразная для функции , то есть

. (11)

Тогда

. (12)

Действительно, по определению, неопределенный интеграл от функции по аргументуравен:

.

Так как то, разделив обе части приведенного выше соотношения наа, получим формулу (12).

Пример 1..

Пример 2.

.

Пример 3.

4.3. Метод замены переменной (метод подстановки)

Одним из основных методов интегрирования является метод замены переменной или метод подстановки. Удачная замена переменной позволяет в ряде случаев упростить подынтегральное выражение, а в простейших случаях – свести интеграл к табличному.

Пусть требуется найти интеграл

,

причем непосредственно подобрать первообразную для функции не удается.

Сделаем замену переменной в подынтегральном выражении, положив

, (13)

где и ее производная- непрерывные функции и существует обратная функция.

Тогда

, (14)

а

=. (15)

В выражении (15) после интегрирования необходимо подставить в правую часть вместо переменной t первоначальную переменнуюх, выразив ее из соотношения (13).

Для того, чтобы доказать справедливость соотношения (15) нужно показать, что производные от его правой и левой частей равны.

Продифференцируем левую часть:

.

Правую часть продифференцируем по хкак сложную функцию, где- промежуточная функция отх, а ее производная вычисляется как производная обратной функции:.

Тогда,

.

Поскольку производные равны, то формула (15) справедлива.

Функцию необходимо подбирать так, чтобы интеграл, стоящий в правой части формулы (15) можно было вычислить.

Замечание. Иногда при интегрировании бывает целесообразнее делать подстановку вида

, (16)

где

. (17)

Поменяв местами в формуле (15) буквы хиt, получим:

=где. (18)

Пример. Рассмотрим пример 3 и применим общий метод замены переменной.

.

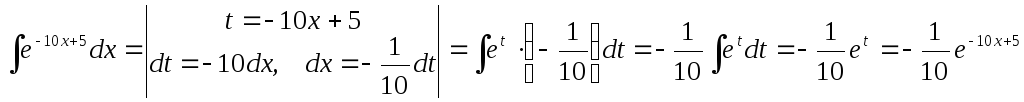Пример 4.

.

Пример 5. .

Пример 6. .

Отметим, что можно было явно не выписывать подстановку, а воспользоваться свойством 6 инвариантности формул интегрирования.

4.4. Метод интегрирования по частям

Данный метод следует из интегрирования формулы для дифференциала произведения двух функций.

Пусть u иv– две дифференцируемые пох функции. Тогда дифференциал произведения этих функций равен:

или.

Проинтегрируем последнее выражение:

. (19)

Формула (19) называется формулой интегрирования по частям. Поскольку произвольная постоянная входит в интеграл, стоящий в правой части, то в формуле (19) она не записывается, а добавляется к конечному выражению после интегрирования.

Из структуры формулы (19) видно, что множитель u, стоящий в левом интеграле, заменяется наdu, то есть дифференцируется, а множительdv – заменяется наv, то есть интегрируется. Поэтому, можно ожидать, что упрощение интеграла в левой части произойдет либо от дифференцированияu, либо от интегрированияdv. На практике, упрощение зачастую происходит путем дифференцирования.

Таким образом, если в подынтегральном выражении имеется множитель, упрощающийся при дифференцировании, то его принимают за u, а все остальные множители, включая дифференциалdх – заdv. Отметим, что иногда для получения окончательного результата требуется применять формулу (19) несколько раз.

Следующие виды интегралов удобно вычислять по частям: