2. Свойства неопределенного интеграла

1. Производная от неопределенного интеграла равна подынтегральной функции:

. (4)

Действительно, дифференцируя выражение (3), с учетом (1) получим:

.

2. Дифференциал неопределенного интеграла равен подынтегральному выражению:

. (5)

По определению дифференциала и свойству 1, имеем:

.

3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная:

. (6)

Рассматривая функцию как первообразную для некоторой функции , можно записать. Найдем дифференциал обеих частей равенства. На основании свойства 2, дифференциал левой части будет равен подынтегральному выражению. Тогда . Отсюда.

4. Постоянный множитель можно выносить за знак интеграла:

. (7)

Равенство (7) означает, что правая и левая его части являются семействами первообразных от одной и той же функции. Тогда, в силу (1), для доказательства этого равенства необходимо показать, что производные от обеих частей равны.

Продифференцируем левую и правую части равенства:

. .

Производные от обеих частей равны, значит равенство верно.

5. Интеграл от алгебраической суммы двух и более функции равен алгебраической сумме интегралов от этих функций:

. (8)

Доказывается аналогично предыдущему.

6. Свойство инвариантности формулы интегрирования.

Всякая формула интегрирования сохраняет свой вид при подстановке вместо независимой переменной любой дифференцируемой от нее функции, то есть, если

, (9)

то

, (10)

где- любая дифференцируемая функция отх.

Это свойство дает возможность применять приведенную ниже таблицу интегралов не только при интегрировании по независимой переменной х, но и по любой другой дифференцируемой по независимой переменнойх функции, что расширяет применение таблицы основных интегралов.

В рассмотренном выше примере, когда , а первообразная ,то есть , вместо независимой переменнойх может стоять любая дифференцируемая функция отх, например,. Тогда неопределенный интеграл будет иметь вид:

.

Заметим, что интеграл равен рассмотренному интегралу .

Воспользовавшись тем, что , то есть, вносяпод знак дифференциала, мы свели вычисление интеграла от тригонометрической функции к интегралу степенной функции. Необходимо так стремиться преобразовать подынтегральное выражение, чтобы оно приняло вид известного интеграла, например, табличного.

3. Таблица основных интегралов

1. ; 9.;

2. ; 10.;

3. ; 11.;

3.а; 11.а;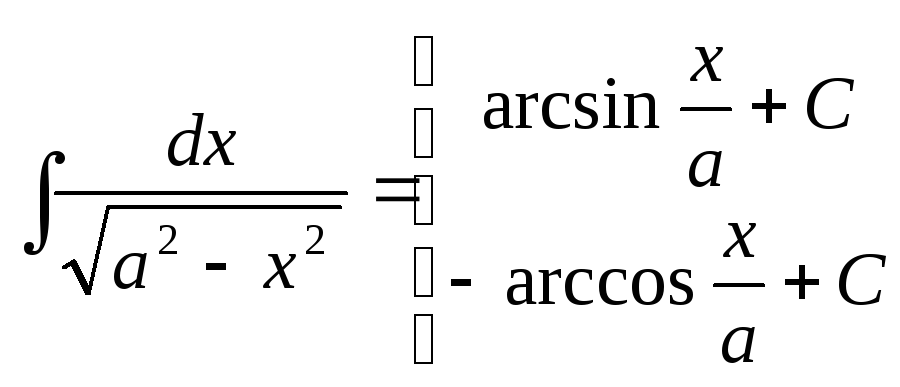

3.б; 12.;

4.; 12.а;

5.; 13.;

6.; 14.;

7.; 15.;

8.; 16..

Замечание.В таблице производных нет выражений для производных от функций, стоящих в правых частях формул 11.а, 12.а, 13, 14, 15, 16. Это интегралы от часто встречающихся функций. В справедливости формул легко убедиться путем непосредственного дифференцирования.

Например, дифференцируя правую часть формулы 13, получим:

. Отсюда .

4. Основные методы интегрирования

4.1. Непосредственное интегрирование

Этот метод состоит в непосредственном применении таблицы интегралов и их свойств. Если же подынтегральное выражение не является табличным, то необходимо путем тождественных преобразований привести подынтегральную функцию к табличному виду.

Вычислить следующие интегралы.

Пример 1. .

Решение. Представим интеграл от алгебраической суммы в виде суммы интегралов (свойство 5), вынося постоянные множители за знаки интегралов (свойство 4) и применяя формулы 2 и 3 таблицы интегралов, получим:

=

Замечание. Здесь и далее произвольные постоянные, входящие по определению в каждый интеграл из суммы, объединяем в одну произвольную постоянную.

Пример 2. .

Решение. Производим почленное деление, выносим постоянные множители, пользуемся табличными интегралами 3 и 6:

=

.

Пример 3. .

Решение. Воспользуемся выражением для косинуса половинного угла:.

.

Пример 4. .

Решение. Воспользуемся основным тригонометрическим равенством:

=.