
- •Міністерство освіти і науки, молоді та спорту України
- •Математична обробка результатів вимірювань
- •Лабораторна робота 1 Визначення прискорення вільного падіння за допомогою математичного маятника
- •Теоретичні відомості
- •Опис приладу та методу вимірювання
- •Хід роботи
- •Обробка результатів вимірювань
- •Лабораторна робота 2 Вивчення фізичного маятника
- •Теоретичні відомості
- •Визначення моменту інерції фізичного та оберненого маятників
- •Опис приладу
- •Хід роботи
- •Обробка результатів вимірювань
- •Лабораторна робота 3 Визначення моменту інерції тіла динамічним методом
- •Теоретичні відомості
- •Лабораторна робота 4 Вивчення основного закону обертального руху твердого тіла на хрестоподібному маятнику
- •Теоретичні відомості
- •Опис приладу та методу вимірювання
- •Хід роботи
- •Лабораторна робота 5 Вивчення власних коливань зосередженої системи
- •Теоретичні відомості
- •Опис приладу
- •Хід роботи
- •Лабораторна робота 6 Визначення абсолютної та відносної вологості повітря
- •Теоретичні відомості
- •Опис приладу та методу вимірювання
- •Хід роботи
- •Лабораторна робота 7 Визначення коефіцієнта внутрішнього тертя рідини методом Стокса
- •Теоретичні відомості
- •Опис приладу та методу вимірювання
- •Хід роботи
- •Обробка результатів вимірювань
- •Лабораторна робота 8 Визначення відношення питомих теплоємностей газу методом адіабатичного розширення
- •Теоретичні відомості
- •Опис приладу та методу вимірювання
- •Хід роботи
- •Лабораторна робота 9 Визначення питомої теплоємності металів методом охолодження
- •Опис приладу
- •Хід роботи
- •Лабораторна робота 10 Визначення універсальної газової сталої
- •Теоретичні відомості
- •Опис приладу та методу вимірювання
- •Хід роботи
- •Лабораторна робота 11 Визначення коефіцієнта внутрішнього тертя, середньої довжини вільного пробігу та ефективного діаметра молекул повітря
- •Теоретичні відомості
- •Опис приладу
- •Хід роботи
- •Обробка результатів досліду
- •Густина сухого повітря за різних температур
- •Тиск і густина насиченої водяної пари за різних температур
- •Психрометрична таблиця відносної вологості повітря, %
Лабораторна робота 5 Вивчення власних коливань зосередженої системи
Прилади та матеріли: прилад для вивчення коливань, набір пружин і важків, секундомір, пристрій для вивчення загасаючих коливань.
Теоретичні відомості
К
Рис.
5.1
в)
а
б
Р
в
Рис.
5.1
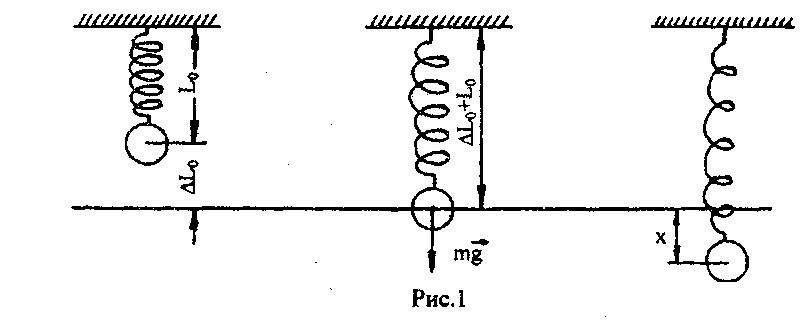
![]() (рис.5.1,б).
У стані рівноваги сила тяжіння mg
врівноважується силою жорсткості
пружини kΔL0
(рис.5.1,б).
У стані рівноваги сила тяжіння mg
врівноважується силою жорсткості
пружини kΔL0
![]() .
(5.1)
.
(5.1)
Якщо змістити вантаж від стану рівноваги на відстань х (рис.5.1,в), то видовження пружини буде ΔL0 + x. Проекція результуючої сили на вісь X матиме значення
![]() .
(5.2)
.
(5.2)
Враховуючи умову рівноваги (5.1), одержимо F = – kх, де k– коефіцієнт жорсткості пружини; х – зміщення. Знак "мінус" означає, що зміщення і сила мають протилежні напрями.
Під
дією сили пружності F
вантаж буде рухатися до стану рівноваги
зі швидкістю
![]() ,
яка
весь час збільшуватиметься. При цьому
потенціальна енергія пружної системи
буде зменшуватися, а кінетична –
збільшуватися. Набувши стану рівноваги,
вантаж продовжуватиме рухатися по
інерції. Цей рух буде сповільнений
і закінчиться тоді, коли кінетична
енергія повністю перетвориться на
потенціальну. Такий же процес матиме
місце й у разі руху вантажу в зворотному
напрямку.
,
яка
весь час збільшуватиметься. При цьому
потенціальна енергія пружної системи
буде зменшуватися, а кінетична –
збільшуватися. Набувши стану рівноваги,
вантаж продовжуватиме рухатися по
інерції. Цей рух буде сповільнений
і закінчиться тоді, коли кінетична
енергія повністю перетвориться на
потенціальну. Такий же процес матиме
місце й у разі руху вантажу в зворотному
напрямку.
Якщо тертя в описаній системі відсутнє, її енергія зберігатиметься і вантаж буде рухатися як завгодно довго, отже, виконуватиме вертикальні гармонічні коливання.
За
другим законом Ньютона рівняння руху
для вантажу має вигляд
![]() .
Перетворимо це рівняння до вигляду
.
Перетворимо це рівняння до вигляду
![]() ,
,
позначимо
![]() ,
тоді матимемо
,
тоді матимемо
![]() .
.
Рух вантажу можна описати лінійним однорідним диференціальним рівнянням другого порядку. Розв'язок цього рівняння матиме вигляд
![]() ,
(5.3)
,
(5.3)
де
а
–
амплітуда
коливання;
![]() –
фаза
коливання;
–
фаза
коливання;
![]() –
кутова
або циклічна частота; t
–
час;
–
кутова
або циклічна частота; t
–
час;
![]() –
початкова
фаза коливання в момент часу
t
= 0.
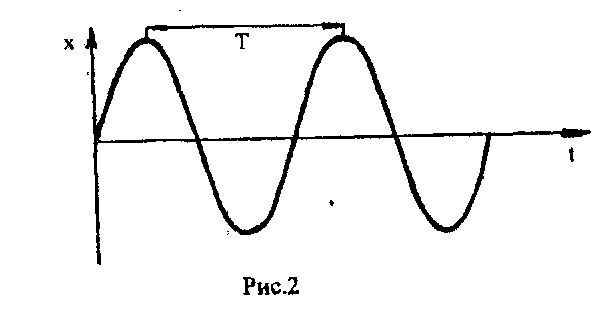
Графік
такого коливання наведений далі (
рис.5.2).
–
початкова
фаза коливання в момент часу
t
= 0.
Графік
такого коливання наведений далі (
рис.5.2).
Рис.
5.2
Кутова
частота
![]() пов'язана з періодом коливаньТ
співвідношенням
пов'язана з періодом коливаньТ
співвідношенням
![]() .
(5.4)
.
(5.4)
Підставляючи
![]() у
вираз (5.4),
одержимо
у
вираз (5.4),
одержимо
![]() .
(5.5)
.
(5.5)
За наявності сил тертя в системі енергія коливальної системи зменшується. Якщо втрати енергії не поповнювати за рахунок роботи зовнішніх сил, коливання важка будуть згасати і рівняння його руху матиме вигляд
![]() ,
,
де
![]() –
сила
тертя;
r–
коефіцієнт сили тертя.
–
сила
тертя;
r–
коефіцієнт сили тертя.
Перепишемо
це рівняння у вигляді
![]() ,
позначимо
,
позначимо![]() ,
,
![]() ,
одержимо
,
одержимо
![]() .
.
Рівняння матиме такий розв’язок
![]() ,
(5.6)
,
(5.6)
де
а0
–
початкова
амплітуда в початковий момент часу; е
–
основа
натурального
логарифма;
![]() –
коефіцієнт згасання.
–
коефіцієнт згасання.
Позначимо
![]() ,
тоді
період коливань дорівнюватиме
,
тоді
період коливань дорівнюватиме
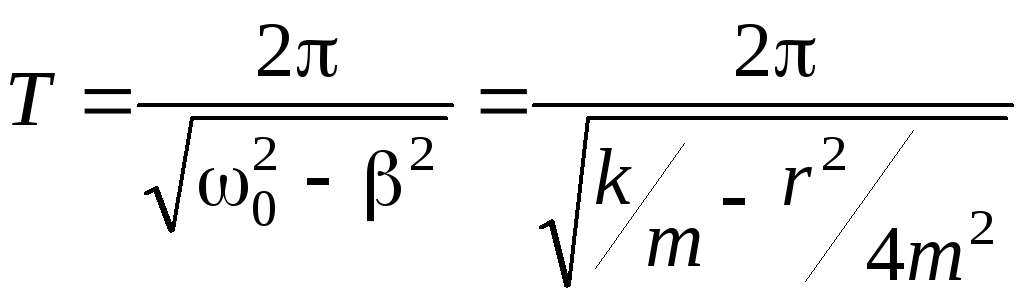 .
(5.7)
.
(5.7)
Таким чином, рух вантажу являє собою гармонічні коливання частотою ω з амплітудою, яка змінюється за законом
![]() (5.8)
(5.8)
Графік такого коливання наведений далі (рис.5.3).
Рис.5.3
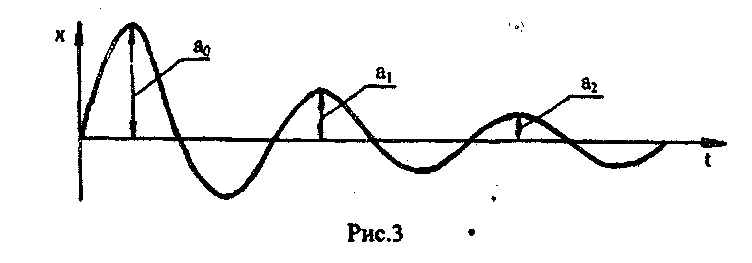
Амплітуди
коливань утворюють геометричну прогресію,
тобто, якщо
![]() ,
то
,
то![]() і т.д.
і т.д.
Логарифм відношення двох послідовних значень амплітуди, відмінних одна від одної на час, рівний періоду Т, називають логарифмічним декрементом згасання і позначають λ.
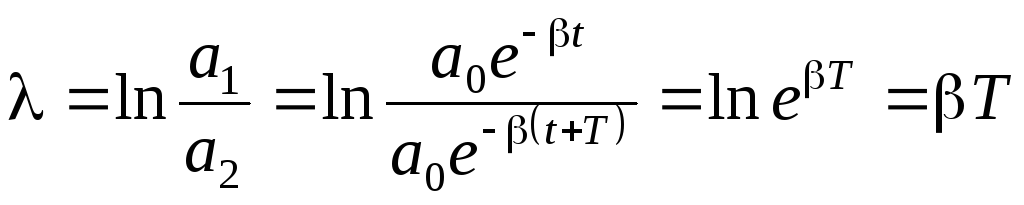 .
(5.9)
.
(5.9)
Підставляючи
вираз (5.9) у рівняння (5.8) отримаємо
![]() .
.
Звідки
![]() .
(5.10)
.
(5.10)
